重尾分布稳健位置度量的优点
有些分布,如 Pareto 或 Cauchy 分布,发生“罕见”事件的概率相对较高。当数据服从这样的重尾分布时,非稳健的位置度量(如样本均值)表现不佳。这种情况下,最好使用更稳健的位置度量,如中位数或双权位置 (biweight location)。
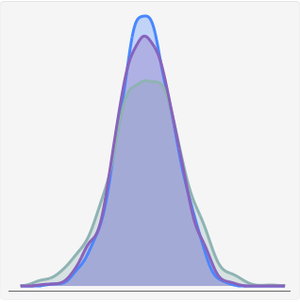
将 Cauchy 分布的 PDF 与相应的 NormalDistribution 的 PDF 进行比较,该 PDF 没有“胖”尾。
显示完整的 Wolfram 语言输入
“胖”尾部分布的特征之一是有些矩(如均值)没有定义。因此,样本均值不可靠。
查看用不同度量计算根据 Cauchy 分布所得数据的位置度量的不同表现。
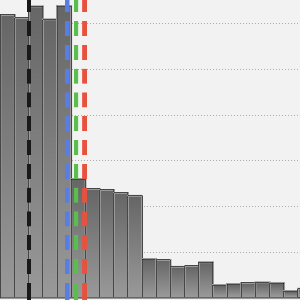
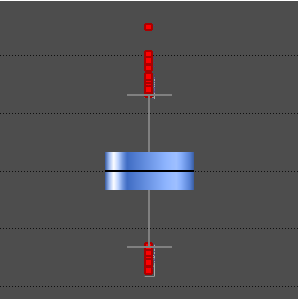
用均值(非稳健)、中位数(稳健)和双权位置(稳健)计算中心位置。
稳健的位置统计结果“平均”更接近重尾分布的中心位置。
显示完整的 Wolfram 语言输入
对于正态分布的数据,双权位置与均值非常接近。