SI 단위와 물리 상수
2019년 5월 20일부터 7개의 SI 기본 단위(초, 미터, 킬로그램, 암페어, 켈빈, 몰, 칸델라)가 물리의 기본 상수의 정확한 값에 근거하게 되었습니다. 이미 정확한 값인 광속과 더불어 플랑크 상수, 볼츠만 상수, 아보가드로 상수, 밀리컨 상수 (기본 전하로 더 자주 불리워짐)가 2019년 5월 20일을 기점으로 정확한 값을 갖게 되었습니다.
이러한 정의적 물리 상수는 "PhysicalConstant" 영역에 자신의 실체 클래스를 가집니다.
이러한 새로운 값은 관련 특성을 검색하여 정리할 수 있습니다.
물리 상수 및 새로운 SI 단위 값 사이의 관계를 유지하기 위해, 지금까지 불확실성을 포함하던 물리 단위 (예: 조셉슨 상수)는 정확한 값을 갖게 되었습니다. 또한, 이전에 정확한 값을 가지고 있던 몇 가지 물리 상수 (자기 상수 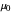 , 전기 상수
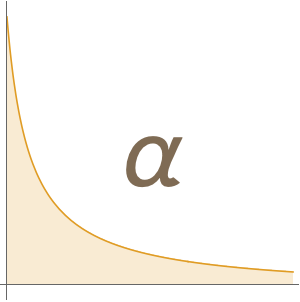
, 전기 상수 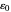 )는 유한한 불확실성을 갖게 되었습니다. 특히 이러한 수량의 불확실성은 미세 구조 상수
)는 유한한 불확실성을 갖게 되었습니다. 특히 이러한 수량의 불확실성은 미세 구조 상수 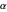 및 뤼드베리 상수
및 뤼드베리 상수 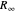 의 거듭 제곱의 불확실성으로 인해 종종 결정됩니다.
의 거듭 제곱의 불확실성으로 인해 종종 결정됩니다.
10개의 중요한 물리 상수의 불확실성을 새로운 SI로 계산하기 위해 "EquivalentForms" 특성을 사용할 수 있습니다. 이 특성은 기존의 SI에서도 새로운 SI에서도 참으로 유지되는 상수 사이의 관계를 부여합니다.
모든 불확실성을 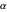 및
및 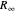 의 불확실성에 의해 나타내기 위하여 모든 형태를 다양한 물리 상수 사이의 다항식 관계로 변환합니다.
의 불확실성에 의해 나타내기 위하여 모든 형태를 다양한 물리 상수 사이의 다항식 관계로 변환합니다.
각 상수에 대한 그뢰브너 기저를 사용하여 모든 방정식을 정확한 상수 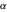 및
및 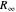 만을 포함한 최소 형식으로 간략할 수 있습니다. 이렇게 하면 목록에 있는 다른 상수의 불확실성에 주로 무엇이 관련되어 있는지를 판정할 수 있습니다.
만을 포함한 최소 형식으로 간략할 수 있습니다. 이렇게 하면 목록에 있는 다른 상수의 불확실성에 주로 무엇이 관련되어 있는지를 판정할 수 있습니다.
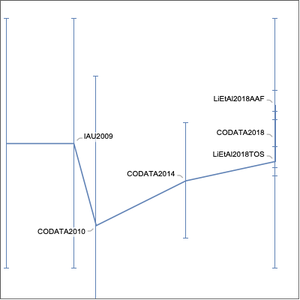
다음은 이렇게 얻어진 다양한 상수의 이전 및 새로운 불확실성의 결과를 정리한 것입니다.
이처럼 2019년 5월 20일에는 전자의 질량이 5월 19일보다 25배 작은 불확실성으로 지정할 수 있게 되었습니다. 일수 상수에서 정확하게 알 수 있는 경우도 있지만, 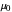 과
과 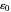 은 미세 구조 상수에서 계승된 상대적인 불확실성과 함께 불확실해 졌습니다.
은 미세 구조 상수에서 계승된 상대적인 불확실성과 함께 불확실해 졌습니다.