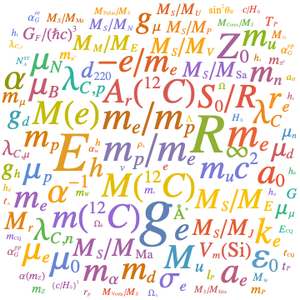물리 상수의 불확실성

"PhysicalConstant" 실체 영역은 자연계의 많은 기본 상수를 포함하여 물리 상수에 대한 자세한 도표를 포함합니다.

물리 상수의 종합적인 특성 집합도 이용할 수 있습니다.

이러한 특성의 핵심은 최상의 측정값 및 불확실성입니다. 이 예는 다양한 물리 상수가 매우 다른 불확실성을 갖는 것으로 알려져 있는 것을 보여줍니다.

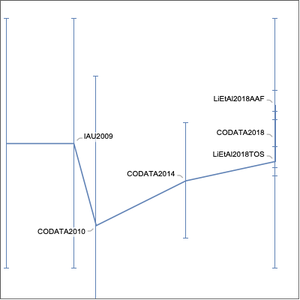
만유 인력의 법칙에서 볼 수 있는 중력 상수 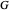에 대해 생각해 봅니다.

다음은 현재 알려진 가장 좋은 값과 그에 관련된 불확실성의 목록입니다.

상수의 값은 계산을 쉽게 하기 위해 에 대해 다음과 같이 불확실성을 포함한 여러 가지 형식으로 반환될 수 있습니다.

물리 상수의 상대적인 불확실성을 찾기 위해 먼저 모든 상수 값을 꺼내고, 정확한 값을 갖는 불확실성이 불명확하거나 원자 단위 및 자연 단위에 해당하는 상수를 제외합니다.

상대 불확실성이 정밀도로 변환된 새로운 데이터의 목록을 작성합니다. 몇 가지 중요한 상수를 골라 냄으로써, LabelVisibility 옵션을 사용하여 결과의 플롯에서 그것들에 확실히 라벨을 붙입니다.

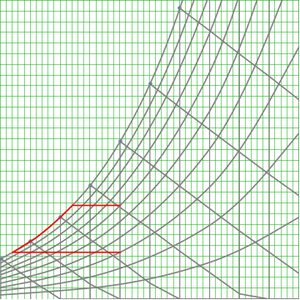
이제 표로 만든 정수의 정렬된 정밀도를 플롯합니다.

이 플롯은 다양한 상수가 알려진 정밀도의 큰 차이를 한눈에 보여줍니다. 예를 들어, 중력 상수는 자연의 기본 상수의 중심적인 집합에서 잘 알려져 있지 않은 것인 (소수점 이하 단 4.3 자리까지만 알려져 있다) 반면 전자의 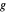인자는 놀랍게도 12.4 자리까지 알려져 있습니다.

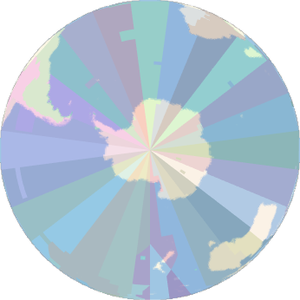
물리 상수의 기존의 정밀도는 기호의 크기에 알려진 정밀도로 가중지를 부여한 워드 클라우드 (변형을 더 강조하기 위해 3 승하여 정확도를 조정)를 사용해도 깔끔하게 시각화할 수 있습니다.