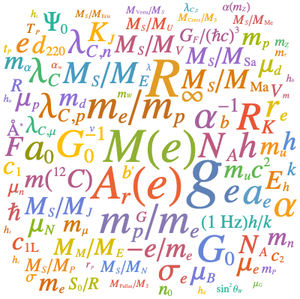SI 单位和物理常数
从 2019 年 5 月 20 日开始,七个 SI 基本单位(秒,米,千克,安培,开尔文,摩尔和坎德拉)将以物理基本常数的精确值为基础。除了已被视为精确值的光速之外,在那一天,普朗克常数、玻尔兹曼常数、阿伏加德常数和密立根常数(通常被称为基本电荷)将具有精确值。
这些物理常数在 "PhysicalConstant" 域中有自己的实体类。
可以通过 "ValueAssociation" 属性获取建议的定义,得到它们的新值
为了保持物理常数和新 SI 单位值之间的关系,将赋予当前具有不确定性的物理常数(例如约瑟夫森常数)精确值。另外,当前具有精确值的物理常数(例如磁和电常数 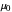 和
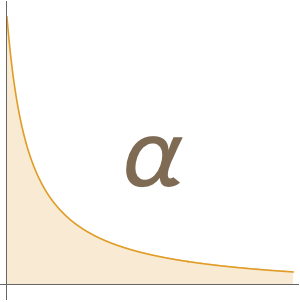
和 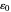 )将具有有限的不确定性。具体来说,这些量的不确定性通常取决于精细结构常数
)将具有有限的不确定性。具体来说,这些量的不确定性通常取决于精细结构常数 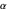 和里德伯常数
和里德伯常数 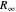 的幂的不确定性。
的幂的不确定性。
如果想计算新 SI 中 10 个重要物理常数的不确定性,可以使用 "EquivalentForms" 属性,该属性给出在新 SI 和旧 SI 中都成立的常量之间的关系式。
为了用 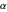 和
和 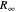 的不确定性表示所有的不确定性,将所有形式转换为各种物理常数之间的多项式关系式。
的不确定性表示所有的不确定性,将所有形式转换为各种物理常数之间的多项式关系式。
对于每个常数,现在可以使用 Gröbner 基数将所有方程简化为最简形式,仅包含精确常数以及 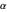 和
和 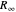 。这将帮助我们确定列表中其他常数对不确定性的主要贡献。
。这将帮助我们确定列表中其他常数对不确定性的主要贡献。
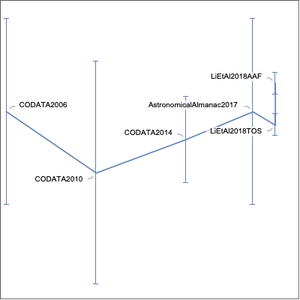
以下是对如此操作获得的各种常数的新旧不确定性的概述。
因此,在 5 月 20 日,电子的质量将被指定为具有比 5 月 19 日的值小 25 倍的不确定性。一些常数将被视为已具有精确值,但是 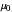 和
和 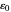 将变得不确定,具有从精细结构常数承继的相对不确定性。
将变得不确定,具有从精细结构常数承继的相对不确定性。