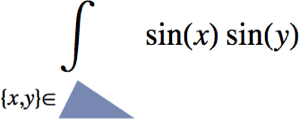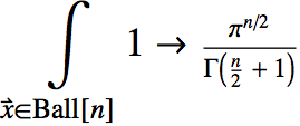Basic and Formula Regions
Version 10 adds full support for basic and formula-based geometric regions. Basic regions are common and easy to specify. Formula regions are flexible and have great descriptive power. Basic and formula regions can be used to compute exact or approximate solutions or results involving parameters, often in any number of dimensions. Basic and formula regions fully support the geometric region framework, including computing properties (area, nearest point, etc.), being used as input to solvers (optimization, solving PDEs, etc.), and discretization.
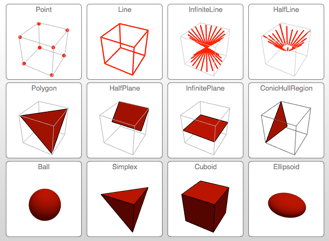
- Most existing 2D and 3D graphics primitives are basic regions.
- Side-side-side, side-angle-side, etc. triangles. »
- Infinite and half-infinite line. »
- Infinite and half-infinite plane. »
- Infinite and half-finite linear cone. »
- Parallelogram and generalized parallelepiped.
- Polyhedra including tetrahedron, hexahedron, prism, and pyramid.
- Ball in any number of dimensions. »
- Circumsphere specified by
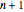 points in dimension
points in dimension  . »
. » - Ellipsoid in any number of dimensions and any orientation. »
- Simplex in any dimension and representing any dimension object. »
- Implicit regions specified by inequalities and equalities. »
- Parametric regions specified by parametric functions. »
- Boolean combinations and transformations. »
- Full support for computing properties such as membership test, minimum distance, nearest point, measure (length, area, volume), centroid, etc. for all regions. »
- Symbolic and numeric integration over regions.
- Symbolic and numeric optimization over regions.
- Symbolic and numeric equation solving with region constraints.
- Numeric solution of partial differential equations over regions.
- Support for discretizing into mesh regions in dimension 1, 2, and 3.