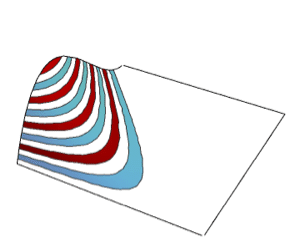
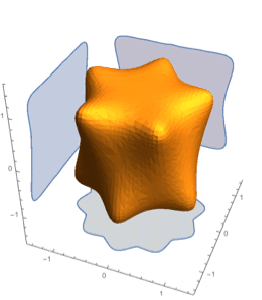
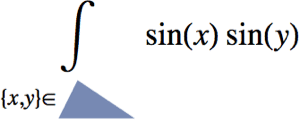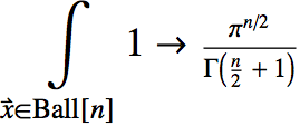Integrate over Regions
Integrate over basic geometric regions.
| In[1]:= | X |
| In[2]:= | X |
| Out[2]= |
Visualize the region.
| In[3]:= | X |
| Out[3]= | 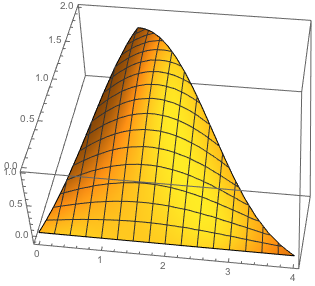 |
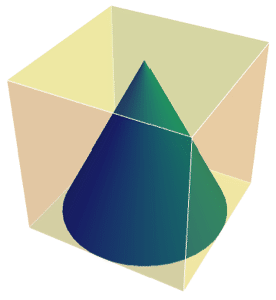
Integrate over regions in higher dimensions.
| In[4]:= | X |
| Out[4]= |
| In[5]:= | X |
| Out[5]= |
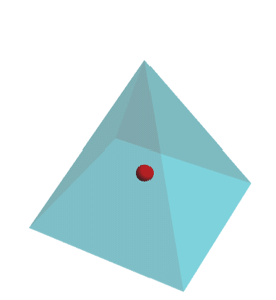
Integrate over implicit regions.
| In[6]:= | X |
| In[7]:= | X |
| Out[7]= |
| Out[8]= | 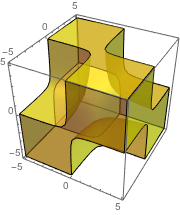 |
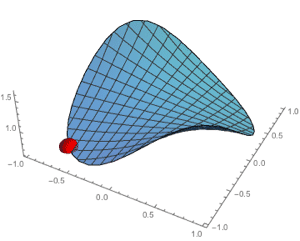
Integrate over parametric regions.
| In[9]:= | X |
| In[10]:= | X |
| Out[10]= |
| Out[11]= | 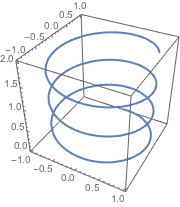 |