一个体积的主轴
要确定空间中体积的分割方向,可通过计算其密度分布的第二中心矩并导出相应特征向量. 以下为计算中心距和体积方向的简短脚本.
| In[1]:= |  X |
定义计算阵列矩的函数.
| In[2]:= |  X |
将体积转换为数据阵列矩,其索引与图形坐标对齐.
| In[3]:= | X |
计算牙齿密度的一阶和二阶矩.
| In[4]:= | X |
| In[5]:= |  X |
计算中心距矩阵的主轴.
| In[6]:= |  X |
| Out[6]= |
显示牙齿的主轴.
| Out[7]= | 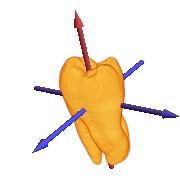 |
要确定空间中体积的分割方向,可通过计算其密度分布的第二中心矩并导出相应特征向量. 以下为计算中心距和体积方向的简短脚本.
| In[1]:= |  X |
定义计算阵列矩的函数.
| In[2]:= |  X |
将体积转换为数据阵列矩,其索引与图形坐标对齐.
| In[3]:= | X |
计算牙齿密度的一阶和二阶矩.
| In[4]:= | X |
| In[5]:= |  X |
计算中心距矩阵的主轴.
| In[6]:= |  X |
| Out[6]= |
显示牙齿的主轴.
| Out[7]= |  |
Questions? Comments? Contact a Wolfram expert »