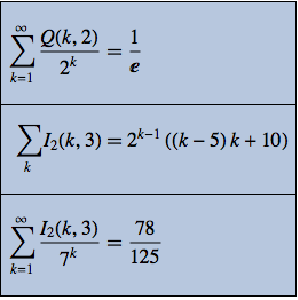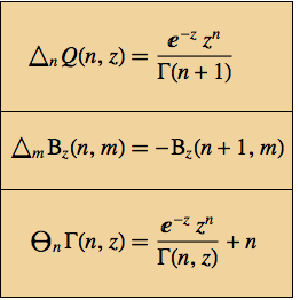Encuentre soluciones simbólicas para ecuaciones diferenciales de retardo 

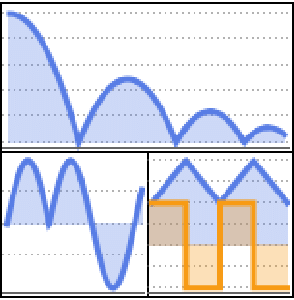
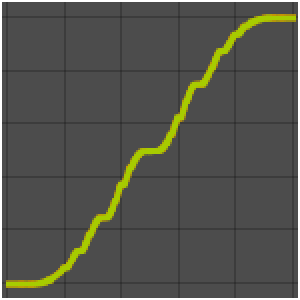
Resuelva una ecuación de retardo de primer orden usando DSolve.

In[1]:=

X sol = DSolve[{x'[t] == x[t - 1]^2, x[t /; t < 0] == a t}, x[t], {t, 0, 2}]

Out[1]=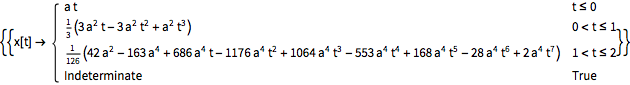

In[2]:=

X Plot[Evaluate[Table[x[t] /. sol[[1]], {a, 1, 5}]], {t, -1, 2}, Exclusions -> None]

Out[2]=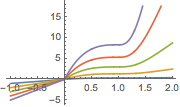

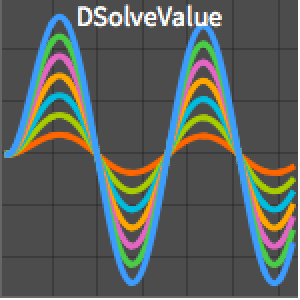
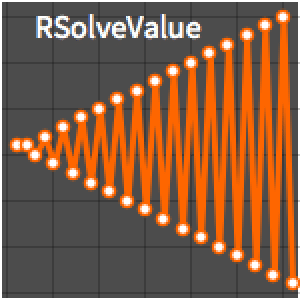
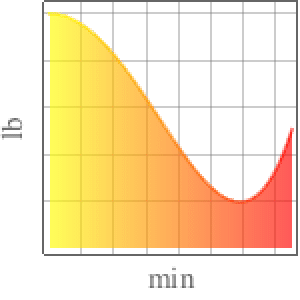
Resuelva una ecuación de retardo de quinto orden.

In[3]:=

X sol = DSolve[{x'''''[t] == -x[t - 2], x[t /; t <= 0] == a t}, x, {t, 0, 10}];

In[4]:=

X Plot[Evaluate[Table[x[t] /. sol[[1]], {a, 1, 4, 1/3}], {t, -1, 10}], WorkingPrecision -> 400, PlotRange -> All, Exclusions -> None]

Out[4]=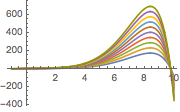

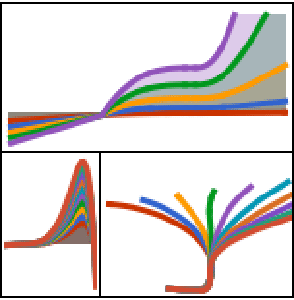
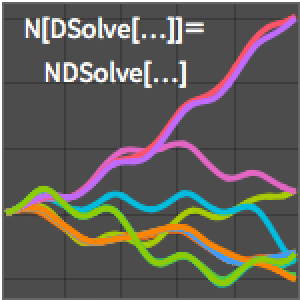
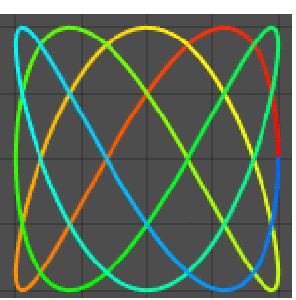
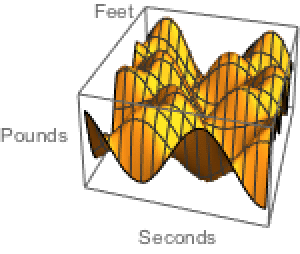
Resuelva un sistema de ecuaciones de retardo.

In[5]:=

X eqns = {x'[t] == a y[t - 1] + y[t - 3], y'[t] == x[t - 1], x[t /; t <= 0] == t, y[t /; t <= 0] == t^2};

In[6]:=

X sol = DSolve[eqns, {x, y}, {t, 0, 5}];

In[7]:=

X ParametricPlot[ Evaluate[Table[{x[t], y[t]} /. sol, {a, -1, 2, 1/3}]], {t, 0, 5}, WorkingPrecision -> 200, Exclusions -> None]

Out[7]=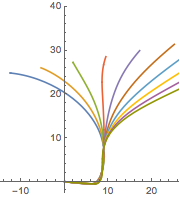