地球の曲率を調べる 

地球の曲率がその表面の経路にどのような影響を与えるかを示す．

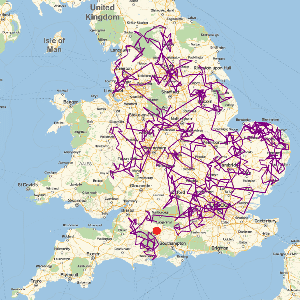
エッフェル塔を出発して，順番に東西南北のそれぞれの方向の測地線に沿って100km移動する経路を定義する．

In[1]:=

X start = Entity["Building", "TourEiffel"][ EntityProperty["Building", "Position"]]; d = Quantity[100, "Kilometers"]; path = {GeoDisplacement[{d, "North"}, "Geodesic"], GeoDisplacement[{d, "East"}, "Geodesic"], GeoDisplacement[{d, "South"}, "Geodesic"], GeoDisplacement[{d, "West"}, "Geodesic"]};

4つの部分の経路を描画し，ズームインして，地球の曲率が原因でその経路が閉じないいことを検証する．

In[2]:=

X GraphicsRow[ Apply[GeoGraphics[{Red, PointSize[Large], Point[start], Darker[Green], Thickness[Large], GeoPath[{start, path}]}, ##1] &, {{}, {GeoCenter -> start, GeoRange -> Quantity[3, "Kilometers"]}}, {1}]]

Out[2]=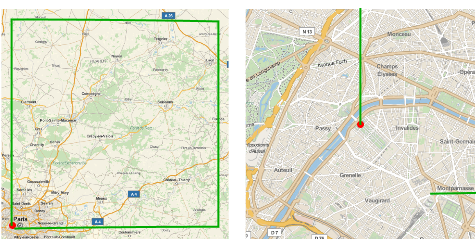

出発点と終点の間の距離を求める．

In[3]:=

X GeoDistance[start, Last[GeoDestination[start, path]]]

Out[3]=

今度は測地線の代りに航程線（一定の航程の曲線）に従う．

In[4]:=

X d = Quantity[100, "Kilometers"]; path = {GeoDisplacement[{d, "North"}, "Rhumb"], GeoDisplacement[{d, "East"}, "Rhumb"], GeoDisplacement[{d, "South"}, "Rhumb"], GeoDisplacement[{d, "West"}, "Rhumb"]};

終点の緯度は出発点の緯度と一致するが，経度は一致しない．

In[5]:=

X GraphicsRow[ Apply[GeoGraphics[{Red, PointSize[Large], Point[start], Darker[Green], Thickness[Large], GeoPath[{start, path}]}, ##1] &, {{}, {GeoCenter -> start, GeoRange -> Quantity[3, "Kilometers"]}}, {1}]]

Out[5]=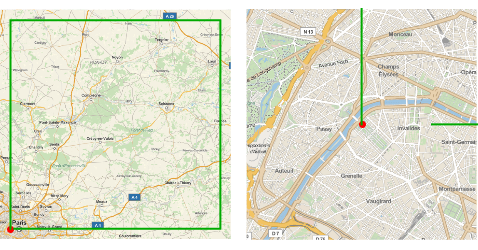

出発点から最終点までの距離を求める．

In[6]:=

X GeoDistance[start, Last[GeoDestination[start, path]]]

Out[6]=