New in Mathematica 9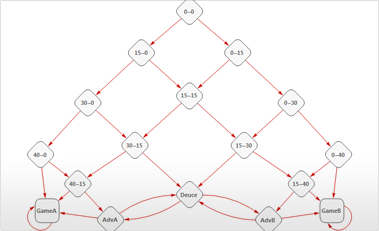
Markov Chains and Queues
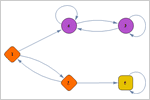
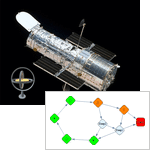
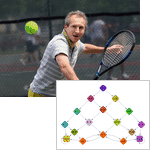
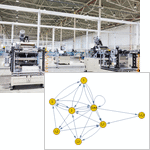
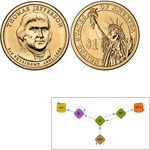
Mathematica 9 provides fully automated support for discrete-time and continuous-time finite Markov processes and for finite and infinite queues and queueing networks with general arrival and service time distributions. The symbolic representation of these processes in Mathematica makes it easy to query for common process properties, visualize the process, simulate process paths, perform parameter estimation, do probability operations on time slices, and compute the stationary distribution and first passage time distribution. The seamless integration with Mathematica's powerful hybrid symbolic-numeric computation engine makes modeling real-world Markov and queueing examples easier and more flexible than ever before.

- Discrete-time and continuous-time finite Markov processes.
- Use matrices or graphs to specify Markov transition probabilities.
- Direct support for first passage time distributions for path transitions.
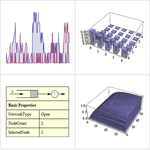
- Extensive support for structural, transient, and limiting properties for Markov processes.
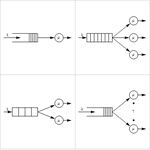
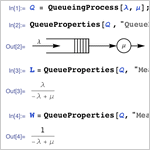
- General queueing process, single or multiple server, finite or infinite system size.
- Ability to use general arrival and service time distributions (M/M, M/G, G/M, G/G, ...).
- Full support for open (Jackson) or closed (Gordon-Newell) networks of queues.
- Extensive support for structural and performance properties, such as waiting times.
- Markov processes and queues fully supported as random processes.