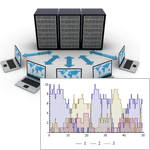
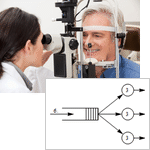
Цепи Маркова и теория массового обслуживания
В системе Mathematica 9 введена полная автоматизированная поддержка конечных цепей Маркова в дискретном и в непрерывном времени, а также конечных и бесконечных очередей и сетей массового обслуживания с общими распределениями времен поступления и обслуживания. Символьное представление этих процессов в системе Mathematica облегчает операции нахождения распространённых свойств процесса, генерирования и визуализации случайных траекторий процесса, выполнения вероятностных операций на временных срезах процесса, нахождения стационарного распределения и распределения времени первого достижения границы. Слаженная интеграция с мощной гибридной символьно-численной вычислительной подсистемой системы Mathematica, облегчает моделирование примеров цепей Маркова и примеров очередей, взятых из жизни и делает моделирование более гибким, чем когда-либо.
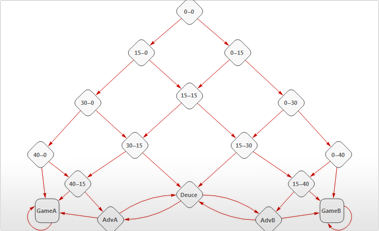
- Конечные цепи Маркова в дискретном и непрерывном времени.
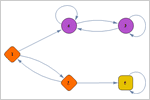
- Возможность задания вероятностей переходов в цепях Маркова с помощью матриц или графов.
- Непосредственная поддержка распределения времени первого достижения границы в цепях Маркова.
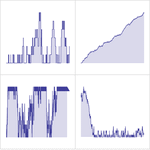
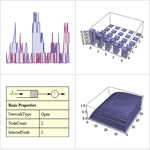
- Обширная поддержка структурных, переходных и предельных свойств процессов Маркова.
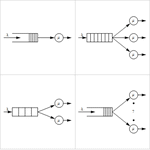
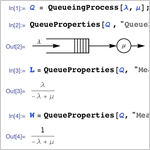
- Процессы массового обслуживания общего положения, с одним или несколькими обслуживающими узлами, с конечным или бесконечным размером системы.
- Возможность использования произвольных распределений для времени поступления и времени обслуживания (M/M, M/G, G/M, G/G ...).
- Полная поддержка открытых (сеть Джексона) или замкнутых (сеть Ньюэлла-Гордона) сетей массового обслуживания.
- Обширная поддержка структурных и эксплуатационных свойств таких, как времена ожидания.
- Полная поддержка цепей Маркова и процессов теории массового обслуживания как случайных процессов.