集団免疫の不確実性
SIR(感受性保持者,感染者,免疫保持者)モデルのダイナミクスを調べることは,パンデミックの制御には欠かせません.すべては疾患の伝染を測定する再生産数(R0)という有名な概念で始まります.ガウス分布や一様分布等の潜在的な分布モデルを含むR0を解析することが,公衆衛生の効果的な応答,ワクチン戦略,政策作成についての情報を得る上で重要な役割を果たします.
感受性保持者,感染者,免疫保持者の人口動態のモデリング
SIRモデルは,ワクチンプログラムにおける感受性保持者,感染者,免疫保持者の人口間の複雑なバランスを描写して,集団免疫に意味のある見識を提供します.
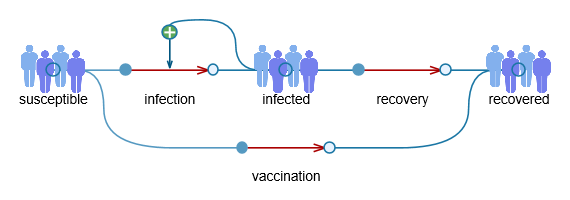
ワクチン下における病気の進行を表すSIRモデル.感受性保持者から感染者になって免疫保持者になるまでの変化を,ワクチンにより感染せずに回復できる場合を含んで示している.
流行の変化
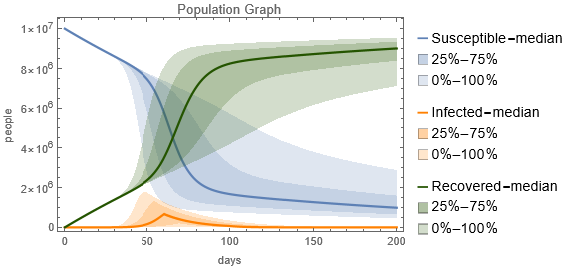
毎日のワクチン接種率を0.5%として,200日にわたる感受性保持者,感染者,免疫保持者の人口の変化を詳しく見てみます.この視覚的な解析は伝染病の経過を追跡する道具であり,現在の健康対策の効果に対する明確な視点を提供し,適応型の戦略の必要性を強調します.
R0が20%の一様分布に従う不確実性を持つSIRモデルは,時間の経過に伴う感受性保持,感染,免疫保持のそれぞれの段階の人数の平均および範囲を描写する.見て分かる通り,感染患者が最も多い時間と日付はR0に大きく依存する.

SystemModelUncertaintyPlot関数を使うと簡単に不確実性解析が実行できる.
システムでガウス分布に従う不確実性を調べる
R0の他,平均感染時間も集団免疫の動態学では重量な役割を果たします.この場合,不確実性は,再生産数および平均感染期間の両方の分散が20%のガウス分布に従うと想定されます.
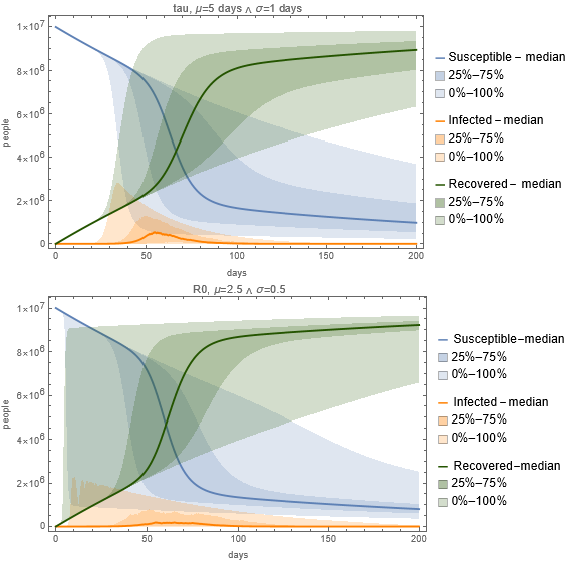
平均感染期間が5日で分散が1日をモデル化した上のグラフと,平均R0が2.5で分散が0.5の下のグラフの流行曲線は,病気の分散の異なる動態を示している.
ワクチンの有効性と医療の限度
SystemModelUncertaintyPlot関数を使ってワクチンの有効性の不確実性を解析することは,最適なワクチンの選択およびリソースの配分の鍵となります.このアプローチは,伝染病管理におけるワクチンの有効性および医療の対応能力の重大な影響を強調します.
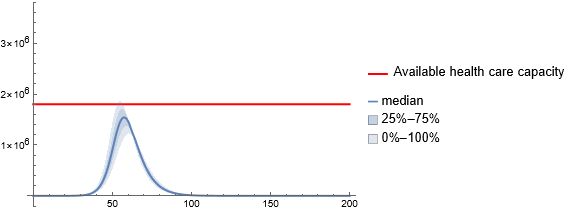
ワクチンの有効性と医療の対応能力の使用状況における20%の不確実性の影響は,医療の受入れが需要に見合っていないことを示す.
Wolfram System Modeler
評価版
ご購入
System ModelerはWindows,macOS,
Linuxで
日本語と英語でご利用になれます »
ご質問やコメントはWolframエキスパートまでお寄せください »