Running the Numbers on the 2015 Chicago Marathon
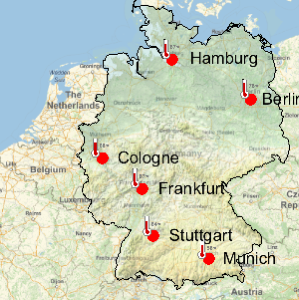
The 2015 Chicago Marathon drew 45,000 runners to Chicago on October 11, 2015. More than 37,000 completed the race, and details of each runner's performance were carefully recorded. Explore and visualize characteristics of the runners and their performances using a custom entity store containing this data.
Load an entity store of the marathon from a ResourceObject.
marathonEntityStore = ResourceData[
ResourceObject[
Association[
"Name" -> "2015 Chicago Marathon Data",
"UUID" -> "7dc77972-cfc3-48dc-8d08-0292c6d2a929",
"ResourceType" -> "DataResource", "Version" -> "1.0.0",
"Description" -> "2015 Chicago Marathon participant data",
"ContentSize" -> Quantity[1990.2215919999999`, "Megabytes"],
"ContentElements" -> {"Content"}]]]
Register the store for this session.
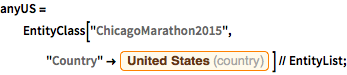
PrependTo[$EntityStores, marathonEntityStore];Extract the total numbers of runners and, using an implicitly defined entity class, the numbers of male and female participants.
EntityValue["ChicagoMarathon2015", "EntityCount"]
Table[EntityValue[
EntityClass["ChicagoMarathon2015", "Gender" -> gender],
"EntityCount"], {gender, {Entity["Gender", "Male"],
Entity["Gender", "Female"]}}]Select five random runners.
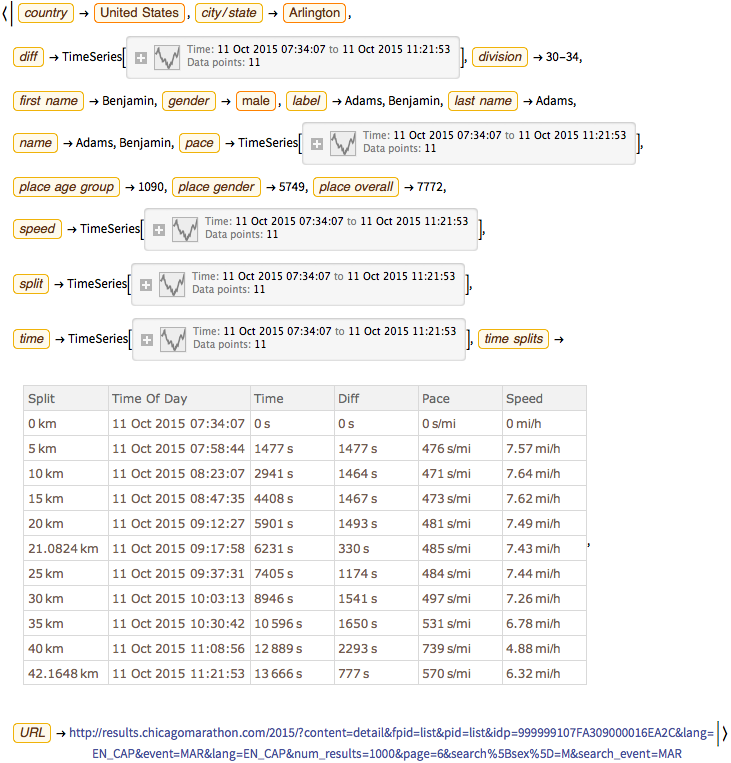
RandomEntity["ChicagoMarathon2015", 5]View stored properties for a particular runner.
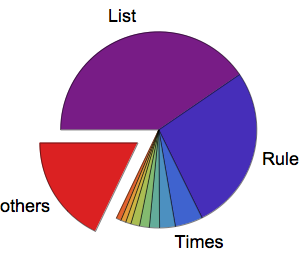
Entity["ChicagoMarathon2015", "Runner145"]["PropertyAssociation"]Extract tallies of runner nationalities and make a table of the most common nationalities.

nationalityTallies =
Reverse[SortBy[
Tally[EntityValue["ChicagoMarathon2015",
EntityProperty["ChicagoMarathon2015", "Country"]]], Last]];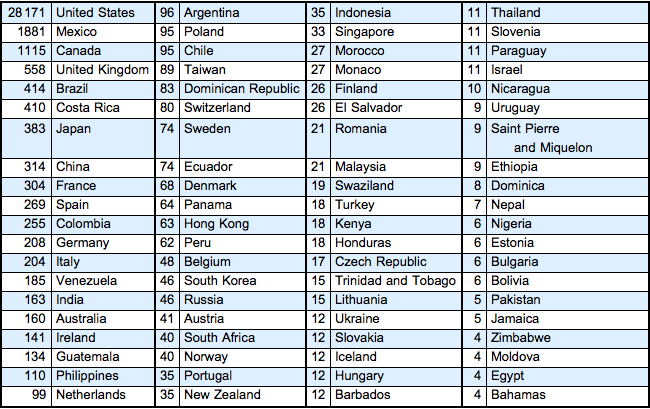
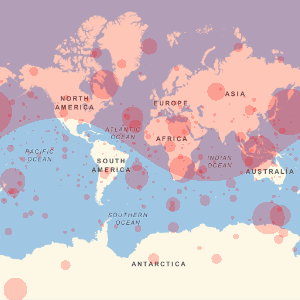
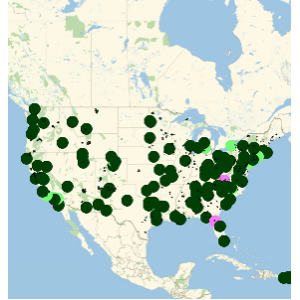
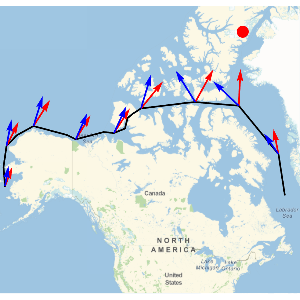
Visualize geodesic paths from all countries of origin to Chicago.

With[{chicago =
Entity["City", {"Chicago", "Illinois", "UnitedStates"}]},
GeoGraphics[{Darker[Green],
GeoPath[{chicago, #} & /@ nationalityTallies[[All, 1]],
"Geodesic"]},
GeoRange -> "World",
GeoProjection -> "Robinson",
GeoCenter -> chicago]]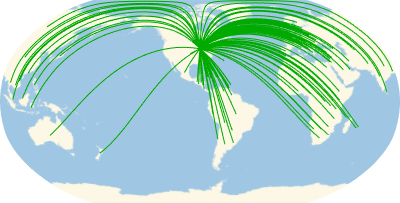
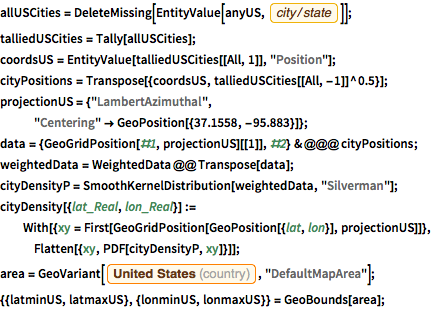
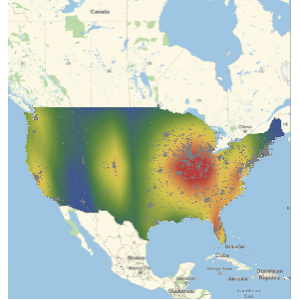
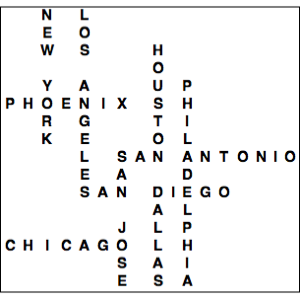
Construct a heat map of the US showing home locations for American participants.

Find the numbers of runners per variation from split mean.
allkm = Table[
Normal[allTimeSplits[[i]][2 ;;, "Time"]], {i,
Length[allTimeSplits]}];allsplitbins = DeleteMissing[Transpose[allkm], 2];meanall = Table[N[Mean[allsplitbins[[i]]]], {i, Length[allsplitbins]}]marathondistances = (allTimeSplits[[1]])[All, "Split"] // Normal
differencesall = Table[{marathondistances[[i + 1]],
allsplitbins[[i]] - meanall[[i]]},
{i, Length[allsplitbins]}];
allHistograms =
Histogram[#2, {60}, PlotLabel -> NumberForm[#1, {3, 1}]] & @@@
differencesall;Generate histograms for each split.
Grid[Partition[allHistograms, UpTo[3]]]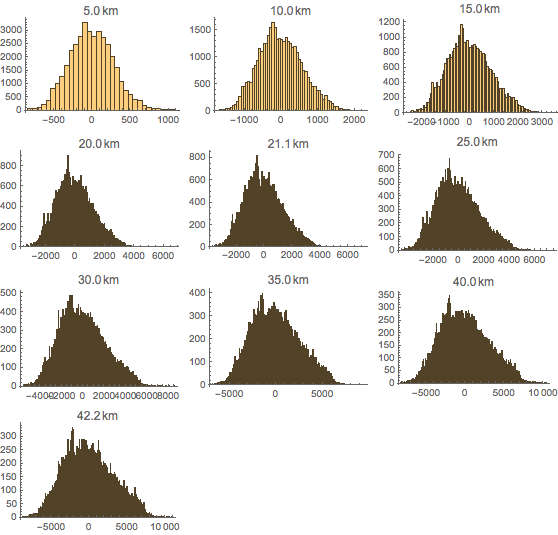
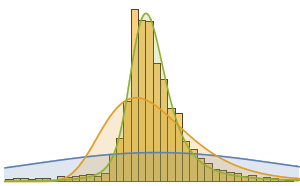
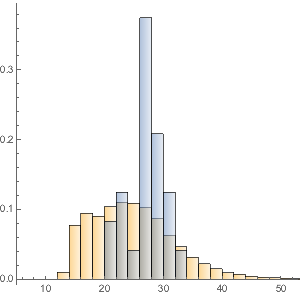
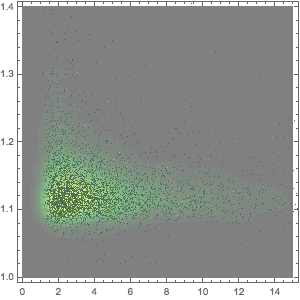
Plot a smooth kernel distribution of the differences between runners' splits and means.