Optimize over Regions
Solve constrained optimization problems using region constraints. Region constraints are expressed using 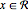 for a region
for a region 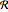 and can be used alone or together with other constraints. Local and global numerical optimization functions as well as symbolic optimization functions support these new constraints.
and can be used alone or together with other constraints. Local and global numerical optimization functions as well as symbolic optimization functions support these new constraints.
Find the minimizing and maximizing point for 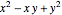 over a disk.
over a disk.
| In[1]:= | X |
| Out[1]= |
| In[2]:= | X |
| Out[2]= |
| In[3]:= | 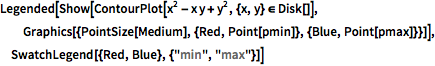 X |
| Out[3]= | 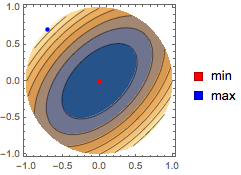 |
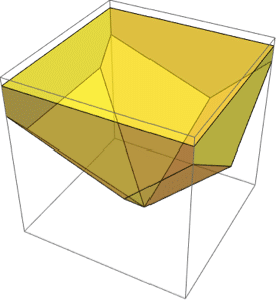
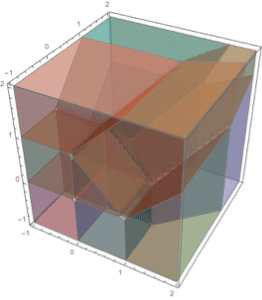
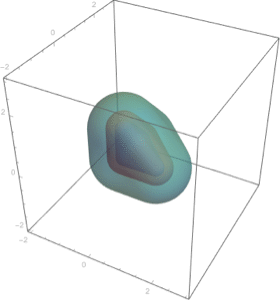
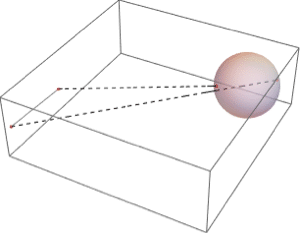
Find the nearest and farthest points between two regions.
| In[4]:= | X |
| In[5]:= | X |
| Out[5]= |
| In[6]:= | X |
| Out[6]= |
| In[7]:= |  X |
| Out[7]= | 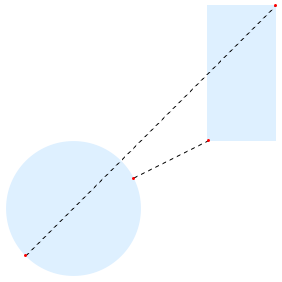 |
Find the nearest and farthest points exactly.
| In[8]:= | X |
| In[9]:= | X |
| Out[9]= | 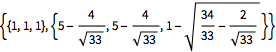 |
| In[10]:= | X |
| Out[10]= |
| In[11]:= |  X |
| Out[11]= | 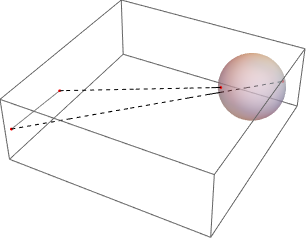 |