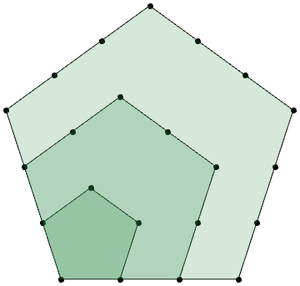
Modélisation de phyllotaxie
L'angle d'or est l'angle qui divise un angle complet 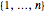 en deux parties conformément au nombre d'or.
en deux parties conformément au nombre d'or.
Extrayez la valeur de l'angle d'or.
In[1]:=
FunctionExpand[GoldenAngle]Out[1]=
Approximez la valeur en radians et en degrés.
In[2]:=
N@{GoldenAngle, GoldenAngle/Degree}Out[2]=
L'angle d'or peut être utilisé pour modéliser les motifs de phyllotaxie.
Out[3]=

Définissez une fonction de phyllotaxie en utilisant GoldenAngle.
In[4]:=
phyllotaxis[step_] :=
Table[Sqrt[i] AngleVector[i GoldenAngle], {i, 0, 1000, step}]Utilisez Graphics pour générer un motif de phyllotaxie à partir de ces points.
In[5]:=
Graphics[{PointSize[Medium], Point[phyllotaxis[1]]}]Out[5]=

Mettez en évidence des spirales de différentes étapes en utilisant différentes couleurs.
In[6]:=
Graphics[{PointSize[Medium], RGBColor[
0.2980392156862745, 0.28627450980392155`, 0.5490196078431373],
Point[phyllotaxis[1]], GrayLevel[1], Point[phyllotaxis[5]]}]Out[6]=

In[7]:=
Graphics[{PointSize[Medium], LCHColor[
Rational[1, 2],
Rational[1, 2],
Rational[1, 3]], Point[phyllotaxis[1]], CMYKColor[0, 0, 1, 0.05],
Point[phyllotaxis[7]]}]Out[7]=

Les motifs de phyllotaxie peuvent également être trouvés dans les têtes de tournesol.
In[8]:=

\!\(\*
GraphicsBox[
TagBox[RasterBox[CompressedData["
1:eJwkmgVUY2feh6edIYYkJFjcQ0KCQwguIYFABEhwd3fGhZnpaHXbrXe7u91u
d7ted5l6p9MRxnC3uHsCfC/9zvnPPe+9B2buOZPnPr/fm0ttG67oevTAgQPj
MHCoaD2aPzbWelyJAieVQ+O93UOdHZKhic7uzjFB20Fw8Wfwh/fIgQP7a3nl
aXnlCWn5cImiV1raJpU0lJfU15W1tVV29dUM9jceH2mfHGqb7Gg43Vh7qrLy
uEIxVlrSJ5F0yKStlbL6WqmqQdHQWtXb1Xysu+up7r6X23tfaep+tbb7D/Km
J4uV5wtkJ9JEXbEZiugkMY2Xh6Mlh+MZGByBnJiWU3myrO/fytFPa0981Hzh
i64nf+x/4XrXc+9XnzmvPNwn6ykvbMjKrUzOlCWnCeMTsrgxCRwWK5pOYzBI
dDqVyaLHpiUVlBS319ee7+p4pb/njb6uP3W1v9DScKVSOSIuUmVnSzIEeQmx
3EQeLzUuISc1ozinsFxUUiVV1FQoG2srG5uV9e3y6jaJsrlA1igQVSXmlLFL
aukv/onwzkfoG1PUuQXy1DTl3c/R//0I8c1PoXcfRM3Ohs0vYWeXIjc2o27c
wLUcYahGeX/6A+yz96FffAq7eztkYQa5uhRkMoebLGijKczhxXj8TJeH7PET
PTskj5/s9FN8fuIP19PGL1wZuHiy69xg22Rj48kG1US5YlB8/Kn0n24l3HkY
c3uKtbgW+3Ap+dZ95tQ98r37xF+vh935EaPXMddXsBtLoZsrSN1mqF6NnL0L
X5kPNepD3c5IzVrwwn3Mwzuh934N+vUn6A/XAm//CFNvYIx6tMsZ7vfhnQ6M
SRdhVGOcVozXhfb7Iv1+otdP9fgovh3S7h7V56dYjWSXneLbpXp3Kf5djtvL
8u2wdvaYYHb3onf3wJrh36Pu+jleD8+9E+Pbi/Xupri8uRZnkclZ6nCL3L5C
m69C52xd1bfOrJQvrJRt6Mo39FXzq+WbulKzt35ZU33vYb5Wl+n2Czz+LKtT
arAqLG6F01duc5R9+A72pWcD3ngr+vk//2ni8WtDlz8fuPhx34V3e87/s2vy
b83HX6kZOS7vqJG2VJQ0VZQ2K0saq4sbKovqVMV1LZLWodKWidKWo5LmI5Lm
o0Wtx8XNh/Or+jOV7RnlLenlzanldenl9VkVdVmqupyqprzqVmFVV2FVb76q
N6eyR6DqTlV2JJe3xCnq46S1yYomfllXZvlYduXxwvonihtfLGp8VdT4ckHt
lbTywWhRGSk7h5iRQcrIImeBRS4hPY+YnoPnZ5FTc0gpmaSUNEJSYlQcNzI2
JoLHxsQyMHGssJjo0BhWKI8ZymWGsumh0bQSRXdpWU+JtLNE1imVtiqkTRXS
+tqy1vbKrv7awZHWU6O9l0d6r/a2X2ltfKym5oRSeaS0tF8i6ZRJ28BPVkkr
6+S1jcq21rqh1tbTLa0Xm1qv1LU+UdX6lKz+8WLVeaHiWLqoMyGzksuXsWJF
5OgMHC0GS6EQOMwUiaq0+5nKI+/Wn7vW/vi1vueu9b/wTuvjT9deOFo92Vk+
rijtKxC1ZebXCTLLUvlFiYnZsbyUGHZsNIvFjI6OiYtPz80pVypGutpeGB/+
3/HDn5488sXRiQ9Gh/7W0f5UZfWARFqTLyxMS0/k8xPSBSnZGQJJgbCsSKIs
lVbKZdXK0uqa0qr64oqGAnl9lqSWL1TFZyhYeTLmM89T3/kw7KvvI6fnKHPL
1O9/xf73g8APP0Ndvxk2M4deWo1aWolcWo4wGLHvf0hvHMr73bPhn7wX8MlH
0BvXg+ankYvzQTodxmQJM5rQNgfa46O5PSSPl+Dx4z27JI+P4PYTnW7y3/7d
Nnzpmf4Lw92T/a2TzZUTqhNPSD//gT23xvt1ivJwlr2+nTKzyHs4Q3twHzfz
kPDrddTdXzBGA21jNXJ7Db29GqzdRBo1yPm78OV5pEGHdNnRmnXE3F3U/V8D
p36G/fIN5MevAhYfoPTbaLMB6fWE+X1YmzlMt4k0aULdDoznNwZ9PrzXR/P4
yP4d4t4e0e3EWww4n4fu3wEYUrx+httL29lh7OzSdn/DcG8vemcPrKk7/mif
j7ezx/Xs8OzOLJNN5HCne/ypTl+hwV61oVcubysXV0vUOonBKd22yObXwLrI
7S/R2KQPZjM3ttI8fjB8pyffbM+3uYVOb4HbJ1xdzvjsffoH/8O99ubAkSd/
Gbr85cDFT/oufNRz4b3O8/9sP/tW08kXqkYnZF3VJe1l0g6ltKNS2lpV2qwq
aVIV1dUWNbSUNPaWNA5KGodEDQMF9X35Nb3ZFe0CRUOavJ4vr02WV6bIqviK
mtSKKn5FdbqyPqOsIausJbO8La2sNUXRnCRviJfWcEurOEVKbkllfGkTX9qf
Jh1OkQ2lyyfSFUf58rFYURMjuwSflh2ZzI9MSo5KTsUmC3Ap6XgwyenYBH5U
bGJkbHxELC+Cx8HEsNAcZmg0HcOlo2NooSwaikkNYpID6aQgGjGQSigprSkt
qZOWNMhKG+XS5gppI7BbnaIRMDhQ1z/adnxi4InxgWcGu59qb7nQUHe6SnVE
Ku0rlfbIZN3y0vry0kqVtLJaUV2ram1oGKprmqhpOKKqP17RcEpeN1lUeTxP
PpRe2MbPbebn1CelV8allLLjspncRFoMi8mPTpYXFvWPVZ79Xe3jrzQ982zz
M5ONT442PdFbd7G+arKs/Ghx8UBuQWt6Ti0/S8nnSxMShbz4zBhuKieOn5iR
V1SqaG1tfmxi9F+PTV6/+tj9KxceXnhs6vTklwNjr9d3HpXXNovLJTmStGwR
P1uYni/MlIjzFcVFFSUl5SXicqlIIS9UlAulFZnFFQJRWXKBLDajhJUpZF64
gnvvk8gPv0D9OoVbXCFPLxC/+Db0vY+Cv7wW9GAGvbwSsb6xz+C6OkKrjnzi
5eSzF3gf/uvRD9879NO3wbOAwblg9TaQINpgQFosofv0ecluL87jj/Lu4IEN
3V6sbxenUcdeev5U12NHWibbmo72nXpa9vG1pIcPyTMLzFu3CQvLtM3tpIUF
+sICYeZ+xPxM1K/X4TN3wi1m4uZqmHotRL0WqN0INGpCFu7BV+ZCDNoQpxWp
WUNM/xp872fYre8Cfvwi4Nb3UPUaWr8VbDEG+/3hHneEWYvWbgTZjBi3He11
Y7yecJ+P4PGQfF783i52x4+1mcJtJvyOn7KzQ/Tv7j89vD7K7i55f/ZoO0B/
e4BH8t4eeccXvbPL8njjrNY0izXB44nz+ROdPqHWVramkS9tyhdWcvXGPKe3
SG8VL20UqQ0Fnt08mzNvaS1vZSnV6U7x+BM8O1l2Z7bNleHyZrk8aUZz1nfX
aLdviefud/zln08NXf24/8r7v9H3Tvv5f7dM/qXx1Mv1xy5WDLWXdiukXQpZ
T4WsRyntrChtLy9pKS9qLBfXVohrasQ1jYVVjblVjTlVjdmqhnRFXaqsNqW0
KrmkIk5SkSRRpkhVCdKKRKkySaZKkqqSS1VJsprE0uq4kipecWWMqIItVDDz
peQcCTNfES+qSxS3xRd1xAvbYvOao7NVFEEBLiktPDYZw00I48WHxyZFxKVg
49Nw8YC+lMiYxDBODIbNDmVFo6NZ+7Jj0VEsaiibBo4hDBKSRkKQ8XAyDkHB
w0k4eUmtTFItk1QqJDXlpY2V0oZaWWODoqmjsnOobmC0beJw78WjA0+N9D3R
1X6hsf50deVRuWKwVNZXUtpZUlInK6ksK1FWlAIfqSormyrruitqexQ1ffLq
YUn1oLCiL0/WnV/SK5KNFSkmxLLRwuKenPyGtGxFUkY2N40bnc1MLE/I7xYp
TtfWAtM+2dr0ZHPzE/VNT9TWX6qsPCOTjueLutPzm9Ny6/mZ1Ul8RWxKcVyS
MC6zKEusUFY2jgwMPT959rOnn5p/7pnVZ55ee+Lpxcee/GX0zBstwycqOttL
muQF1ZlCZaZQlimSZBVLcqWSQoWkWCEpkktEpcUFxUU5oqI0YVFKrjA+K4+d
nsUsKGA+9Sz2vU/DPv4C/fX3obML5OV18p2HuM++Dvz4M+jt26FLy+HrG6jV
zbCF1VCTIeL+bPQLT0f/58+PfvzuoW+/CJx5ELwwG7i+Gqw3IA36YDBOdwSw
jNuD9fqivH6sZ4fo9Ee5fLidPcrnX0t6Tk/Unao5cVn5/S9Jv94mzS+T70zh
Htwnr23Q1jdiVpapK0u4+ZnIxdmoX3+CLTwIt1rxW2uhmo1g9TpgEGHUBC/e
g60BBtXBdnOwegXx4OfAez/Cbnx98PtPDi3eD9FvIfWbCIcFtbMTabeidZvB
4LecljCXNRQw6HGHezw4lzPK74/c24nwubBmLcbtIPv9OL8f7/WTXW7Cjh8Q
hweK3N0Di//nkbi3Q/J7mS4Xz2Lm2Kxxbk+sx59odwl15uItnXBjO3dpma8z
pjk8aQZr/tpm4bY+x+vLcXgztrQ5i0uJVluidyfas5vk8gsczmSXN93hEXh8
gp++Z//5ddS//0X47FPhP94ZOnr5ufYzb7Sd+3vr2beaz/yp/sRztcceUw73
SrvLSrqKS3uk0l55aa8CnEo7y0s7yotaZOJ6WUFNWUGVKk+pzFJWZFao0suU
fKkKcBcvlscWlsaIZLEiRYJYHieWcYvkccWKxOKyuCIFr7icW1TOFZWzCuSM
nBJ6ZjE5Q4Tj5+OTcyipebT0YnqmlJ4moaQU4hMzsbH88JgEDDsOHR2L4YCJ
D+cmRcQmR/CSwjkJmOg4NIuDokeDCWWwUNF0FJOGZFCB/kIYlCAGIZCKhxFx
AYQoCCESRoiqrOgqlzUrJNUKSRXIljWK5np5S1N5c1dV51DD4Fjb6HjXyYm+
i6P9V3s7LjQ3nq2tPVFeMSqRdhcW1YuLqkuKVVJJhUxSJiuRKeTliooaWUWt
pKK+WNleqOwUq/qklRMVteerm56ub32mofV3dY1PVtaclVeMimRNGaLixMLk
WClL0JggOVygPCutvqSofbyi6Zma5mcbGp+srrlQoTheJBnKLOxKE7YLClrS
smuT0pXxmfIUsaqosrmjc+jykVP/vPzEd888d+/p300/+fT9S0/fOvf0j0cu
vd114mLtaIesV1bcmiVuzBBXZYvlOeKSnBKJUFoskhWLpGJhcWGuMC89Jysx
KzMuI4ObnhGdlsKtrWW//lb4fz9Ef/Vj1GfXkL/cilhawS6tE2/ex3z1TdB3
3wbOzYatrgRvaTFLq6Fr60iTDXvnV+JbLzz6wX8CPv8Edu8mfH4ahEO4Xocy
G5F6NcJsQnlA3vMQvR6szxfl8+HcPpzLG+ndITldrJf+WDI2WfbTL4mLi7QH
05Gzs+RbN8IW5ilbatbKKml9gwCS5/J82OpC2O0f4IszKJudoF4DHAVqQBZd
R5i0yKX7AevzAEaEVQffnIPe/S5g6vuAHz89eONLiG49RL8ZaFLDfW601xVi
1gVvLQeBU5c50GkO9DiQLk+EwxHucUXu7obvesKdxki7KdznwXm9ET4vdv+5
4cED4gC/e3uE3/QHPPgbj3662842GVgOB8cDWqE3xWLP0+lz9KY0tTZtZTnW
aExyuuNN1uSNjTStPs/lz3D5BDpT8upqok7P9ezGeHfBMcHhTnR7BMCJ/h3+
/YcZA0cKOg5ndgyl1nbya3qkqoEexeDh8rGTyrHTqpFjZf29kk6VqC2/qE1Y
3F4k6RJLe0tLukulnaXyTrm0XV7UKitskOVVl+aoSrMrSjPKitLkEr5Mmlgs
iS0s4hYUcfJErFwhK7eQlSti5hWBYecVcfOLeYUSrlgaU1jKziumZRaS0wqI
/Fx8chY2Pj2Syw9jJ4WxEtHRCWhmPJoRh2LEomgxSBoHxYhBMbmhLB6GzcNw
4yJ58VHc+DAAIIMXyuCgaNFIChNJYSCptBAaJZhKRNLIwTQigoaDkbAQLO4g
NuqRqIhHw8MbGy7UVB1VlXWVldRWlNbUyBsaFPVN5Q2dVR2D9QOjrSOHO46O
d54a7jnX2znZ0nSirna8vLxfLGnJE9cWiCsLiyqKihWlEplUIpGVyqTy8hJF
eZFCWaioKapqV9SPVLWcbep+rmvwjYGRvw8Ovd3b+0Z71yv1zU8qa48VyRuz
S0VJstiUupj8AUHp0YLys8XVVxRNz1U3v9BQ/7vKystlilPFpeM54oF0UW+G
sDMtrykluzYxtyq9tFnRMDA6fOrVM1c/vvK7H598furJFx88/vupS7+/ee73
3x996j+9F67WHWuVD4hLOsF/WY64PldckSsqySgSZxcV5kgKcyXC7MLc9Lyc
lKzMhPR0nkAQI0iPEfATRsfIf/kX+l//w1z7OfL7XyKvfRs4u4BdWccvrhFu
/Ir89lvE7dvBqyvo7S3Upjp0eRm1rUMaLGHX3oX+9/WAzz+ETt1AAAYXpqFb
64FmI8qgDTZoAj2eyB0fxeMGJEaCzzbQosuNdXlxuzvk9fXob7/mriyTlxYo
i4vEe1ORU7cxq0v47W3qyjJWvY3bXAtfWwpbX8Lc+QG2Mot02HHbq4GAPs1a
sGYNbtKGLN2HbMwjDBq4RQPfeACZ+jrg1lcB3713cOZGoFkDN2zBLDrEjhfj
sAYatwO3l6B2fbDDAHNag9yOUIcN47Rh/N6wXT/aZ8dYtWinDTAY7vVg/L4o
jxs8NMBNRu3uRu7uEXaBBPdIu3vY/SDqZdkMNKed4fHQPT7QBzP0eoHJnKY3
JGysxpgMPKeHa3HEbG6majR8pzfZu8s325O3NQnbmzFeX4xnl+nd4zm9PIcn
yelNd7vi9/biXv5TgaiuvbiloriurKBOnFsryq2T5DdIChqKhY3FwgZRXm1W
Tk1KQWOKuDWrpKNQ2iOW9UpkvaWybpkcTJdc0lZa2CDJrSrMrhRllAtTFQUp
cmFSiZAnFnLy8ti5eezsXHZWDisrl5lVwMzMZ2XlszPzeVkFcXmiOGFRbL6Y
ky1kCHKpqVnEBAE+jo/lpkawk9GseCSdF0yNCSKyEYRoBDE6iMQCE0JlIxmA
wdgwDi+cx4uMjYuMiQuL5qJpHDQlGklmhJDpQWQaAkdGEAgIIj6QhEdQcHBq
FIwYBcVGHoqMOoAOPxCC7ux8s7np2brqM5Xlg0p5R7WitaGspbG8oUPVBhgc
aRk53H70cMfJ4c5TPW3HWhvGaisHyhXdYklzfmFtfqGqQFQuEoNwV1pSXFRa
UlRaKpFIS8QK0LUqSqpbVS0jjT0Xe8ZeHT329sTx948c/Xhi4t2Bob+1d75S
13BRphwoKC0TSNOSK7mZnQlF41nSk8KKi7K6p1X1z1bW/U6puiqTnxFJj+ZI
xnKKR7JEfYKCjtTcpuSCpqyy3or2Y0eOXnnz4nPXrjx//cqLN6+8PHX11XuX
/3D77MvXDj/7165LJ6uPq6RDBaXdwpLOPElTTnFltqg0TVyULhJlFeZlCLPT
crOSsjPjMzNi09Nj0jM4GZmxhbkxzz1HfPN/EX/7N+bza6E3pnDf/BB8+27Y
0ip+fYswNx9+40bIL9fh83Oh62shOj0SeHB1DWUyRem3Iz/+W8CH/3709nXE
4mzg4gx8eQFmMgQbtSG6rUCnDe33krxuoseF9bijfF6y10tweaLcXrzfTzUa
sMvL5NVV/OIS7vZN9Mw9zNZ61NYmaXkJq9dF/bb9gt5cDr37A3RtFum0R6pX
EVpQBteCtOtwszpo+QFkYxGmV8NMW7C1u5CpL6C/fHLw+3cPbs0HmrdhJjXM
bgrc8aAtBoR+DQzUoQ+y62FuO9Jlx9hMoBhidrxovxvpMqJsOrTHub9X43MD
D+Lcrki/L8Lvw+ztRgH97QO4CwCM2tsleJ1kp5XgcZM9nhi7M9loTLDaYi3W
mM01jnqD43VzbE66WhOzuRHvcCd79+Kc7iSDKXFrg+V0snf2GN69aPcu1+Hi
unzxTj9n15+oN3MHjyrL2psqwGewRSVtkErqJJJ6cUldoaRWWFJfIKnLKarJ
Lq7PKmnOlrUXlHVLyvukysGyqmFV1XBd9UBtdV+VskclbQOtsFRUW5yrEgoU
uQKFMFUqjBfnx+TnsHOy2NmZ0VnZzMwsekYmLT2blZEdk57Ny8iOz86Ny8uP
zS2IycxhpWXQUgTEBD6WlxLBSQhjxgHrAdyCyBwELhqOZcKwDASBEUhkhlAA
g0CFMWFsbgSXGxETE86OwbBiQulsFJkRTKQG4ikIHAUaRYJG4iERWCgOCyVE
QckR4AiJingkLOIAKuxAEGZ45Jvu7n+3NL1UV3O5RnWiTjXRoOpvUra1q9r6
antHmocAgxOdp0Y6T/e3HW9vONxQPaJU9EkkbfnC2rx8ZUFheUGhrLCwSCzK
LyoWFpcUFZcWga4lLi+T1jZXto22DF0dPPbH45P/PXnuk1Pnr508/enhif/2
D7zZ3PaMompCKKvLkhamViSltyTmD6UXHcuTThZXXJarriqqrsrLLxRJT+WX
HM0sOZIHCBUP8wv7BMKujOLuPNW4suPc+NFn/njp5a+vvnrz8it3Lrx888Kr
t869+tOJlz4YfuaFlgsDFcdLZaNCWZ+wtCtL0pgjUYE4mi4uThcVZgpz+HmZ
STnZ8fuTk5Cbk5CXG5+fkzo8yHv3I9o/Pgj7239DPvo89MadqF+nIq7fRE3P
Ra2sRW1qSHengqduI+/eQayuoDTbSI02ZH09aGsT6fRErc6jP/rnwR+/hC3M
wpZmAIZQgxZh0gdpNuAWQ4jXHen3kl2O/Q+21wMwxHm8IJEC0RC8HppOQ9ja
iJqfi7h3G7M8Habdxq+uktaWcEYdVr2O1G6Gbi8jH/wE214MdVgiQOnTrMI1
q0Gg6Jk1QcsPIZuLMMM2VLcasHwTcuuzgB/fP3jrc6hlO8i8vS9HtyPY4wg2
bcPVixDLNsymgTqMcJcNaTMibQaUxxG640V5rEibJthpCvW7MF4nxueN8uzf
Z8SOL2zHF7q3B7IoYBC3D+Be1K6f5rHT3E6818twOpNNhiS7LcZhZ+rUjI1l
sssZ7XTRdNrotSW2xcb17nFd3iSbLVa7HW0xAQDp/j2Gb4/j9sW4vDxQJN3+
6L099kcfiluGRrvGertGRztGRjsG+9v6+9oG+tv7B9p621t6mho76+s66mo6
q2q6VTU9ytrB6rqR2sbDLc1Hu9qO9XccHWgf72sd6agbaK3qqS/vqCppkAsr
i3MrijLkomRJAS8/k52bEZ2TycjKpGVkUAUCiiCTlZbJE2TGZmTyMjPic7IS
srN5mensdAE9NY2UkBIF+h0od4xYJJWDJLORJE4Qnv0bg3QEjgYYRFLZKAYb
zWJjojmAvghOTHg0B83kIOnRIWRaIJ6KiCTBw4kBGMLBUOwhdCQ0EjAYCSdH
wYnYAGzkIxERB0LDDgRiDh9fHBz5oav7ndbmN+prn66vudhYdbRF1duq6uyq
7h6s7x1vHZ1oPzLaeWqo43RPy6mWuiO1qiG5tFNYWJuXV5GTp8jJL83NExYU
ZBaKQdgTiktERTJQEysUDe01XRMd40+Pnfn7qcufTF79evLKd2ceu3bi9CfD
Y39v7X6+vPaYSN6UJZPwlWmpDYkZ3fzc0czCo/klp8SyyWLZWVHxiQLxRF7R
RIZoQiAcyhAOJosHBcXDmUWjBYqjFY2Tw8OPP3/y+Q/Ov/rtxdd/ufD6D5Ov
fn34hff6n32t+fFJ1fmm8hOSiomisv5saVueBGTRSr5YKhCLBWJRemEBX1iQ
IhQmF4iSC8WphZLU4tLM+sqcv/+H8cn32Hc/x779Xth7n2B+uhE5M0u8dRt9
dwo9Nxe+uY1bXg2/fzf4/lTQ/DRiayNQq0HqdMi1NbjOEOLz4mfvoL7438GZ
e7DlOdjydMD2GtxsDNKsw/TbCJcN5fcS3a4opx3pcaHAx9vvw3l9oHOF+f04
n5uq2YhanMbM3UevL4RqNfilJbx6LdKsj9BshBjU6M3FwJmfodq1ULspYns5
ULMC1S4jjJvAg4HLDwM2FqCGTZh2MWDhJ+gvHx787j+H5n9GOPWAQahVA8og
0m4MNKxA1fMBNjXcqoY6TIF2U5BZC64H+5whPkewQx9s14Z47WivHelzob3u
MI8L0Bfu96J3d8L29sBgd3cifpNgpN8DyiDB6yW5XbEWE8th47hcDLOetL4Y
CUh0eygGHXVtgWbQckHpc/t4DifPqKcbtXT/Dtu/R9nZY3p8LLc3BozHGw1O
DZrYxy50jJy+eOTs+aNnrhw9dfn4mcePn3r8xMknT5186sSJC0eOnhqZmBgc
G+4dG+gc6W4b6Wwb72w/3NF9oq/71Gjv6fH+MxN9J8Z7Dg91jvU3D3bW9Tar
2mvl9ZVFVWUFSmmatDCxKIeXnwE8yMhIp6TxKalp1NQ0Nj89Ni09Lj2dm5kW
myVIyBDEZvA5GWms1FRyXFJUbGI4JwGUOxSNg6SwQwCDhGg4jgHH0YMIjGDQ
9WgsNJMdxgYDGOSEcTgYFjuUwUbRWECCCCwFHo6HovGHULhDIZGQ0AhoBBZO
xAVR8WDgJDyw4aHwsAPBYeOndQMT012937S0/qem9sWqyifqVGcalMNNqp72
qu6+2p6R5sHD7eOHO4+Ndp0ZbDvT1XikqXpYKe8sLqzJzynLzC4VZInTM3Oy
swT5+Vni4jxxSYFYLilWlZU3t9b2jneMPzV+9u9nnvji3NM/nH3yh8mrP5x4
7IuRo2+39T9fVj9eWFafKS/hKzOT6+L5rYkZfYK80dzCifzCw3mFh3Pyx9Ny
h+MLBlOkI/EdZ5PazyeWjcWXjAnqT2cNXs25+seyN9/r+eirgWs/jv9488jP
t0e+vTH08Xdj//hk8Oobyv7L+TXHC+UTotLh7JL2jJIGvrhSUCTjF0kERcWC
4hKBRCaQlAkkFYJSZWZJbY68VnjqhODLn8lf/IT/9Hv6vz8Jf+cjzHc/hC3M
k2YeRty+ibp/F720jNnWYqcfwuZnUTP3YRurwZvrCIMeqVYjNtdDnLZIjwNz
4wvo1I+By3OQlZmAjUW4SRcIAFSvQh2WYDfwiw/rsCHdzhC3K9TnBUkv3ONB
eUEU9BGNmsiVaeTyA5R6Fa1VRywtonVbYWY9OIYY1aGbC4jZX6D6DZTNiNla
gmlXYNolhGkDBky3AhicAxKEbs9CZr+F/fzOoe/+FbA6BXPogAShoPp5nSEW
NVwzH6BdgFi2YFY1zGFEWHXBZjXSYQz0O4NdpiDrNtxpBDCGemzBfne4C8Do
CgUJFsTUvd2I3d3w/aM/7DcGSV4nwevGeb1Mq5HptFPdbqLTSlYvYa0GotdP
sphpa/Nk9QbN7eH5djhOJ9dmI2s2KC4XbWcfQLJvh+r2RLu9HJeX6fUz9vao
X38qGjpx7ORjl85cfOrsxZfOPvbSOTDnXjx/9qWL5165ePals5PPnDx16ciJ
M+NHjw8fmeibGO05MthzrLf/1MDAmfGBMxP9J8f6jg73Tgx2jQB7drX099R1
tlc0N0rrq8Q15TllEoGkILEgg5edyUoXUPkp5JQEampSND+ZJ0iNE6Ry0/cn
VpAam57KEaSyklOocYk4XkIYJz6UzgUMgtgZTAF2iwb6CyIx9zdbaMxQOgvD
ig5ns4EB/1+CGAYLRaWjSPQg0AEjiFA0LgCFPYgEEwk8CIncZzCERgqhEYOp
BAQZB8NhHw2NHD1j6R1fae29Xt/838rKF8sqrlaUn6oqH6kt72tWdnfWdA42
9B1uHTraMT7eeXqkc7K/5VhbzXB1WWepuFaYrcgQFKel5mXws7LTs3Jzs0RF
QrG8SKySSOrkZe0N1QNDbYcvjZz98+mnPr/w++uPPfvL5FM/HL/0ydDxvzQP
PC5vGCworxXIipPKshKqkpIaEtM6krL70nOGs3OGs7KHBDl9aem9KVmdnN+9
IXgwK707I/3kG+Fb/0v/6lr6zV/jZh6ylpail9fZK+uMtS362nb02jZnTROz
ouEsrqdMzaZ88G36pRdzqvuzJPUicU1akTJNXMYvKRfIVBny2kx5Y1Z5W05F
Z46qu6C6r6SlN/+Ntzg/3WF88xP5m1/o738V+e4nmK+voWfn8GvruHt3g2/f
Cp6ZRml0USuryMW5oMWZoKXZoM21YK060GQIAU406EJ8O5j1BdT1TyGrc4iV
aVDf4LotmFGN2FoMsOhRDhvALdzlxAAVAgy9bmDGUK8HaDHY749y24mbc0Gr
D4J16xjtZtjyIsqwFWrShejVgEHU5kLg/E24YQtpNaK3lqCaZahmAWbcAAMF
DK7PQEDO3LgPmf4S8sO/Dn73dsDWDNSmDrJqYC4L1GVFGNbhWw8h+mWIeR1q
18IdhkCrJtiqDnKb4V5rkFMbbNmEuS3BXnsQYBCkU7cd7XehdlzIXcDgTvj+
nsxO+B4Q4m7Unh8wSPR7WXYz3WUhez0kt4eg3ww3aUg+D9XlxKrXqBtLFKcj
2r8X7XEz3U6aUUMy6wi7u5SdXerOLs3jo7i9bA/A0E3b26NZzMmXnm4bP39+
8srl848/f/HqHy5efvXipVcvXXrtyuU/PX7pz1cv/+nShdfOn3v+zOTTJ049
duTUmZETxwdPHh04NTF4emz43PHRc2eGT50YPDbRMzHUMdLTPtTb2t/X0NWt
ammRN1RL6lVClSxLLkotyonNyYhOT6Pxk6kp8fSUOCY/lpuWECdI4gmSYviJ
vN+GnZLITEik8uLx3HgMOy6Mxg2j7GdRFIkRSmGF/Ka/UBoTxWACACNi2Fge
B8vjRXC44dHRaBodRaQicSREBB6GwUOQUQcDIx4NinwUMBgWBcPhA8mE3xgk
hVCJQWQ8nIA9FBHVd9zcNrxY3/WTquFdheo1edmTCsVJZdlYVflAY0V3Z1VH
f33naFPP4bbBiY6jox0nB5oPd9YN11d0yYtqhNklmfyCtOQsQUpGZnpmbl6W
sKRQXF4krhaLm4qlXSrlcEfDkSO9k78/cvXfk899df73P5168svR8//pnHix
uvtUcW1HdrkqpbQgXpoWW54cX5Oc2JTE70jN7E3P7EvL6Odn9idldMfyW5lX
X45b38zd0Ig3DYVbOuH6tnBxlT8zF/3wIXF6Gju/QFhdp6xtMwGGG9vsDQ17
U01Vayk6M2dbx/3xZ/rvXuRVt6QUKfklDZmKttyqblH1gKhmpLjusKTxWHHr
KWnPKcXvX0784gf6L/ep3/yC//kO7bPvie9/Hv7Nd+i7dyO3tfiVVdTUraCp
m8Hrq+E6ffjyQsjKAmr2LmR9KWhrFWbUBRu0gVvrMKs11OPBPPwpaPE2YnUa
ujwNUa9BTWqEGmhrI9BuCXQ5MB53hG1/EeRxBu1vhnhQHifC50HteHE2ddjm
Q5h2DaVeD1tfRBnVSJMmyKgJMmwHbc5Dl24hTOoQmwm5vQgYhGjmoYZViH4N
svLg0CqohDOQ1VsB9z+BfPu3g9f/G2BcQVi3ETYt1G0FxMG1i7CtBwFGwOAq
FGRRqzbIuA63awMBgy493LqJABnVYw10W+Aee4jTEuK2hwIA/c6QPR9mx4cB
KXRfiH6wiNqP0E6S3Ui1Gyk+N8nnxpq1Ubr1KI+T7HZgjVv4rXmK3cLw79I9
XqbbRbEaCIYt/I6XsLf/LT/D46Xtg+kBcZSy46d4vOR//qNi5MLJU5cvnH3i
8QtPvnjpideuXHn98uVXLl/+09Urbzxx9c3HH//rlUt/uXzh9fPnf3/q7JXj
5y4cOX9hdHJyZPLU8NnTI+fOTJw7N3bm9MDxwyCLdoz0tg/1tfb31He0Kpsb
5PVVxbUVwkpZTpk4XVoQX5gRncWnpyXRUuMY/FgaP4YNMOTHcVJ47CQuJ4nH
TuQy47g0LpfIiYlkx4TSOaGU6FAgPhIjhERDUegoKgPDiI6Ijo7gsCO5HGwc
BxvPxcXzorgxYUwGhkpBEchBkXgYMGBI5KOIiAOw8AOwiIMgi2Ki4HhsMI2A
YlCQdDKKSkJSCEFEHBQb1Tymr+ufq+r4ubz+A3nV2xWqP1RWPFFbea6u6lhz
5WBndVdffddwY/dYS99E2+h4+5HB5rGuusFGZUd5SZU4ryQrPT+Vn8UXZAqy
07OFWUJpgbisUFxVKGoSl3TJ5YNVqvH2phPHes4/MXzltYkn/j504c8dx56r
HTovbx8S1tSnl0sTSzPjSlNiy5Niq5Li65OTm5P4bUmCjqT0rkRBT2JmR0xK
S5y4hfHTL6nbOv6WMUdjytUYhVvGok2daG0rc3GJOzNDm36Am5+PXF0nbm6z
t9QAPabGwFQbqBoL2eikmo2MH3/ATpxIkLcVVA7nNx4uaD4pa5uUd14o772s
HLha++Qf8776hv3jHcqt6X0Gf71H/+E2/f0vMN//FHHrVtjGVpTWEDk7g7xz
I3DuYYhOh9GqsatLyKVZ+BLIgYCITdh+79uEa7fhbjfKog2f/Rm+No0AcXR9
HqLfQBi3greWIBY93GYK8nnDbBa4w4YADPpB2POgwcLjAOtQvyNCvxKoWw3a
WkZtLe0DCPg1qgP1m/DtBejKLYR5O8hmDAJr7RJEMwcBTOmWIGv3D609gKzf
hyz9fOjOB4e+eiPg3hcw2xbCsg2Ud8hrCwIL9TREMx1gBPewDrVsA3sGG1Zh
TgPCZQA/CTGvQV3633g0wZymIIclxONA7jhDdoEHPaE7++iF7fpQu/7QfQY9
RJsea9FEeR14nxtnN2B1KxEeO9njirCo8RvTBOM2eXeH4fVT3S6600rSrWM9
DsLeDhYw6PMT3B6yx0nzevD+HTKQ4NSd5NHTA0euHDl7+cTZq1cmrzx95uKz
k4+9dOb8K2cfe/Xy5ReuXv7D5at/vfKbCs+df/HU5OPHz186dvHK4XOPjZ2d
HDk/OXJucvzs2dHTpwePHekZH+oY7msb7Gvp665pbaxoqJFWK4sry4QVJdly
kaAkP7Eog52TyspIYgji6YI4uiCGmcphg0lmsxPY0fFsVhybHhNNYkVH0RkY
IDsqK4REB/QFE2lIMhVFpaHpQH+MKOC+WIAeF5fAAwDi43hYbkw4k4GmkINx
REQ4FhIS+Qg87AAk7MCh8APQsEeCwg+GRsLw2BA6EcWg7g+djAQqJOFh2Kjq
wa3Knlll28/ljZ8p6z+oqftXQ92fmxueb66/3FZ3orN2qK9hcLipf6ypZ6J1
YLxtbLh5uKe+r1nVppJWSYRyED/TMrNSsvipOfwMUUZeaVahPF+kEokbi4o7
iop7iyVDCvlobeXRjprjg3WnjtSfOKYaHZb2dIua67KqpSlleXGlqdySeK4i
lqeKi6+JT6yLS2qMTW7ipbbEprbFC1pjU5pZolbmf96L1uqT1YZEnSVFZ07Q
mVN15nyNSawx5Gt0WZsbyUvzzLlp/MI8dn2TsK2naIxUnQkMQWchGK14qyti
boH49O8TGo/LGs6WdF2q6H+yYujZmrHnm06/1PL+Vwk//0q9eZ9yb47y7S9R
t+/Tp2aYn32D/uE67s5UxPJypNFC2NjEPLwTOHM3aG0pxGQirK8Gbawglh4e
WpuDbSwFGLQwgyZwa/WQSR/kdYeol9DL9yGrs7DVGYhmBWTIwK0FiGk70GqA
eVwhTkeQ1QT1OIO9rkC/BwgR7nJAPS7ErgflMoQY1uBbi0j1KtKsDbRo4KZt
uH4DDpLn2hTCqgm06YNA7ASpUjsDMS1BdAuQ1bsBa/ega1OQhR8gt98L+PL1
gKUbcJsaVD+oUxMAGDSuQDbvHdLOQgz7DELM4FmxiDCtw91GuEMNBWYEYHoM
CHDqAlf0CKclaH+jxh6860YBDPf84Tve0F0fcscL1ninAWfeRHtsUT5XpNOM
0a9hnCaqzxNlN0eoF4i6FarHTd1/yc1N9bhIJk2UVYff28Hv7eJ2d0heD8Ht
JLgcuB0/aWePurODX13IuXlLdftW4+0bfdd/Gf/u+7NffHH5k4+f+9tfn3ru
mRcuXvjDmbN/uHDhL5cuvXHuwgunJp84dvrK0cnzR84/Ng4APHt66OzxockT
w2dODZ082XfkSPfoaGtfb3NPd31nu6qpXl6tkqgU4nJZvqI4U5qfWpydIE6P
yeNHZycxs+IZmbH09BhGKoeZxGYmRLPiWKxYJoPHJDPpOAo9jEhB4clIAjWY
QAnGU4IJVBAyQ2l0NIMWzmZF8WL+H0BCUhwxIY4QH4vj7TMYSqQERRFgGBBB
ww9AMAcOog88gt4/wtCPIMOhkVEhFGIonQoGRacgaaRgEgEWhVUCADunKjtu
VrX+WNd2ra3j8+7Od7s73+rqeLm79Ym+lsnB1qMjLSPjzb3jTZ1jLQMjTQN9
9T2tlW2V0oZScYWwoFiQl5GUk5Kcn5oqTsssScuVZQuV4sIGkaitsLCrQNgv
Eg0WiwflYERDZYX9ZcJORW6LNKNOnKzKii9L5UoTY0riYmScmPKYWBU3oZqb
UMdNrOMk1bFTG6KTG7ipdeThScprryHu3IrWm9laC0tvjjaYOUZzktGarTVn
6U3pJnOO0ZCtUfNXV6KXlgirm/htHVlnJBssBIMVZ7AT9Xa82UpY2ya+/wX9
ykv5489VjLxQM/5Ky8RrA8//u+bGbe7Nh5TpadrsIvWHG7ip+9T5FebPN6O+
+x4zPR25MBuh1WMNJszSXPCDW/ClmRCdJkynDd1cgW4uBu6/prIAUa8HmHSB
mnXI9irEYgzxuFDbS9DVGShohVsLgEG4FlCzDLcZYE5bkMeDMhsC3I4gnwux
4wn2u0LcNpjbgfC7gvyOEPMGfGM+SL0SZNHCLWq4aQtqWIeB5Ln1AGHXIWzg
X1kEUROim4MaFyCArNU7ASt3YKu3ILNfQX7998Fv/3xIP4ewbUPs2zCHNsBt
DtQtBGxNQXSzUMAgUJ5pLVAzD7dtwVw6hGUNql84ZNuEuA0wlxbqMgQCBj22
IB+4N1sgiKNg9ryYHQCjD6TlUL+TYFlHuw0YrzPU44g0rqGcBqzXHea24wzr
RPUC3mUlAcG5vfsbNQ4L1qQGIRa3t4Pb2yP5fESvi+y04ECC3dll7OzSvU4g
yiyPM9frLHZ7pF6vzOMtdXsrXb5mm7NDrTl67/4zH7z7wvNPP3d+8pXjJ147
evKpiePnRo+fGD5xvO/4RPex4e7jg13HhjqPDHUeHuocH+kYHmzq6qhtbVE1
NcjrqoqVMlFZaYG8OFsqTJNkJ4sz44R8TnYiOzeBlZ3AyIqlZ8TQU9n0RBY1
lkGLYVE5TFI0PYpKReMpIVhiYBQ+GEtAYolILAmJpwAPhtJp4Qx6FDsaFxtD
TIwjJseRknnEhBhCXAyOxwljMJF4MiICF4CK2k+hAZh9AMEcQB84hH4kMBwa
HhlIJKBoVBSNsv/ODPAggQAPxynbf1K2/Vjbfau5b6pr8NbA6M3R8euHJ74d
H3l/bOAvY32/H+u9PNp5cqx9dLS5F4TS4caBvrq+9uq2urJqeam0sEiYIcxM
yk+KFyYkiPn8kowseVa+Kj+/vkDYmi/sFAp7hAU9eQVdudmduRkdeRnNOYL6
jNTajORqQbwqlVeeyJXHxpRyYuQMroIZWx6doOIkVLJjq5i8amqCihitpMjb
mS//EffaK4f++SZia5umN9OMVjo4Gsx0k4VrsafpLKlGS5rVmmWxZJotAoOJ
r9HGbmxStzUkvZlkspLMNorJRtZbiDozQaMnzS0wv72R9N7X+X//VPXSe+3v
Xiu4OxM9s0hfWGYurzNuTOFv36VsbLHml0nffhs6PYtZWgzf3Iw0mSMAetNT
iNl7wauLwSYjemsdrtmCrc3AVu9DNxYCdJsQwzZiYwG6Pgdx2hFua9D6TMDa
DGLlIUS3ATFuBWzPQwFQDjPC5wu1GmF2I4AOTOCuO9hrD3TbEF4bHCRAlwG5
uQDXLiFsGoRZDTNvwvSrEPVsgOZhoEMHt2oRgEHTMsQwF2CYh2qmAX3QlV+h
Cz9CHnwa8NNfD/78NsS2DrNvHnKoYXZdgEsH0zyAqqeg2ocBhiWoaQWqXYDr
FmG27UPWrf2/QT8X4FTDgDFdaqhDAxiE+sBTwgL328EDIXDXA0Jp8K4LteMO
3POG27cjnJpQnxXjtWCMq8F2bbjXFe5xYqxqrHYRbzfid3Zw+4HThfc4sYat
cLcdu/fbNxo7frzHTXLZQC4FQqTtv/7tp3odKW5npsud73KJnC6J01nmcMvs
3mK7p9ThqXB6K5z+aoe3c1t3+Mb1yWee6mjrqm3uaWztb2gaqKzrq6npraru
ra7s2X/dUtWprOqoUraoFNWlUpVEoiwRykXZxXnpoqx0cRa/MCMpPy0+n8/J
SWRm8FjZPFZuLDOLR01nkVPo5HgamUcjRzNwDFokAJBIConCB0bgYGH4oEhC
CBYMCUWghNDIoUxqWDQDy2UT42PJAMDUWFIym5jIwsWysBwWhk5DEknwMOzB
EFADIwB3Bw6g9ucgat+JsLAAZAQCiw0hE0OopH0ASQREFA6Giaxo+VDV8nFD
17WuoV+Hxu+MH506duLOqRM3jh+5dmT0P+ODr4/1PjXWdW6sfQIYcKi+b7C+
o7uuua2uoU6lKJNJC0sKBEX8xMKEeHF8YlFSsjRdUJaVU52f11QIABT1Fgp7
hTndOZmd6YJWQUoDP6kmJRH0vsqkuKqkuMpEbkUcp4zLkbNj5DSugsZTMHhl
gEQ6T0mLU5LjyykxCvzIacqbb6Pf+CPsTy89cvN6lNFGMlgoRhtVZyQajCSL
jWl1xektXLM10ebk2xwpNhvfass0mVO1erZWTzNYiEYr1WhlGS1snTF6S8tc
3WAvLbPmF+jTC8xb05zrtxgPZwlLy6TVDcamlvlwnnjnLm5zi7Gtp92eirxz
O3x1FbO2htYb0GYzemU+ZOZu4NJMsHY7yKALUm8gtBuAQdj6NGR76ZBhG765
AF2cCtBvwnzOQMMadB2o8AFka/6QeQuqWYTpVyA2HQyEVZc9yKQJ8DngOy4w
CL8D2AdgCwELnzVwax40PrhVDQPdzbQONSyDQhegngb1DQEuahf2U6hxPsA4
B9WAJ8BNGGBw9puAex8FfPfHg7ffg7vUMMfmIZcW4dRCgOO2pwK09wGJh4xL
UMMiwBkCjuA6qIc6UBIXAhzbEMcWIBFhXoc4DTCfFeE1w/02wCACPB/89sAd
R8iuO2jHibZuID3GUI81yLIebFoO9jlAmQ1zGCL0S+FWzf6Lpn4fDtDncYVZ
tSCFhu36sfvv2Oxg/W6C2w4sGbHjI+7uUnf3yD43z2XNsVvybaYihz3H4chw
OrOdzgK7U2J1lFodZRZHucUutznL7e5Kh7dpfXvg6aeKikrjRMrsotrs4prc
4rqC4vpCUW2BqDJLrMwSl2cLZZkZohR+XkJKbmJidkJcelxseuz+ZCXE5iRx
s+I56TymgBudHcvO47FyOIz0aAqfQUqk4XiUKDYlgkEJI5GQkdjA8Eh4WBQi
DBcYjguOIiBxJBSRhKJSMSCIRtNxPBYlIYaUxCUkc/FJ0fh4EE1ZYSw6mkoJ
wYEgij0UFAE64IFDoQceQe1PAPoANPwRWNihoDA4OiIoEhuMwwfh8YFYHAAW
gopQNv29qvmfTR3v9wx8M3b45tHjt0+evH3m9O2Tx348Ov7B+PBbo30vjHRf
HGo9PNjYO1Df3VvV3qlqbVY1VparZCWleeL8ZFFanCgptig1XiJIlAv4ldnZ
DaKCtiJxX7GoTwwYzAMMdmSkNfOT65ISKxMSVImxytiYCi44xit5cRUxMeXR
MXJqjJzCVYAjlVtGjS2jxJYReeU0fiX+yd9H/vVt2Jt/gb75OuTdt+Gb2yTj
vtr2c6beEGUyE2wujsURqzMyLQ6uzRlrdyZY7UlWe4rFnmqyJBn2g2u03sQ2
mLl6I29bw17biJ5fiZ5dYs0tUabnGHduE2emcUuLlM1NhkZHWd8gPXwQtr5G
0Jvpq1vE2zfDVlZQ6+tIrQZptaA0GyGLD2CL9xBbS3CbGandghnUADHo+n3Y
Jvhsb8A0q9D5W5D1B1CnEeYywLfnDq49hK7dCwAtzLAKHAQ1g+BnQ/g8ISbN
IY8FtuuE77nhPgfMa4V5LRC/FeqzQDVzh3SL+xuYoNOZVgE4MPXDAPUM3GWC
2zQwPWBwEWoA2XIWopmGrNyALl+HzHwVMPU+5OuXHp35Eu7RQh2bAW6QLbUQ
8xJk+06A/gFMBzy4AFPP7u/PmJch9g24cRamu3/IsgRxboFTiH0LYVo95DUi
PEZwD/AdK2LHGeSzw312BHDingfQF+JUB3qMwfZthH4W4jGhvS6k2xxmXA3V
r4R6HWF+b4THGeF1YJ1mtGkTqHP/W8W9PRxoi15QAy2RPjcQJWlvj+5zUyxa
lt2Q7LTx3a4Ut5vvcGRarWKzRWY2K83WGqtDaXOq7I5qh6vW5mqyu1qd3m6t
fuDN17Nq6tgSVaJEFV+sTCxUxOWWxKeIEpKF8akF8cm5XJ6AyU6h02IpNB6V
Ec9gJjAZSSwmn8PO4LIFMSw+m5XGYWfHsPM5nDwOM4NFFTAoKQxCPDWKQ45g
kDAEPDIsKggdCQeDiUKEY4Oj8CE4PIpEBGUQMBjGomG5THI8m5jAIfw22Fh2
JIeJAS2PvL8jCkFGPgr//zL4mwEPoQ9CI8AcgodBAsNhQRFwZGQgOhKBwUJD
o37bOw2rbPxLTfNfmzv+0zf45eHDN0+cuHv61P2zk/dPn7xx7PBnEyP/HO5/
qb/rSnfLeFf9YF9d60Sn8uRwwcWzGVcfT7xwMebwidj6Xl5hHSetPC5elsqT
ZyQrc3MaxcJ2SWGPpLC7pLBLJOwSZbflChrSUqqTk6sSkyrjE1TcOCUnUcVN
VnETlZzYMgZHRmLLiGw5kSMnxSjIPAWJV0FhV5Dz6kmv/SnyrX/C/vbXgL+/
Cf/7Hx+58QPauK82oslG1BsjwVjsBKeHAQKq1ki2OhgOV7TdybU6Yq32hH0S
bXyjOUFvZOsMLJ2eqdFxtjQxq+v0xUXq0jJ1fol8507U9EP84gJ5e4uo0+O1
etLCHGZtJcJgpOgthPnZyKV5lGY7VKMOsRhDbSbU5hJgELY6DTXrgi1mwCDU
sAldvxew+RDICwoy58o9yOIvUOM6zK2HmjdgmzPQpdsQwyrMsB6gXYQb1yBO
I8TvDbIaYA4D1O+E7bphO06YxxzgNUF8ZpjPDIpeAADNsg0Y3P82QTsH3b4f
AJTnMkFtGoh+PsA0DzX+P4MPA1Z+CVj6GfLwy0O33wn46vlDG78EutUBzi0A
4CHn9iHjDEQ7BdPfh+gfQvRzMHCTulmIbQ1qXYXpH0C19w7ZlmH2NYh9HWpc
hljXA3wGuFsX4DPB/Gb4jj3QawFaBLkUvusKcWmDAKFODVQ3DbNvBIIg7bIi
rZto3UKwXQfaYoTHFe4GZrSGmtZRXhtmz48GEgRgel14pyXC5yTs+km7u6Td
HbrTQHEamB470+1MsIEqoS/Q6yUmc5HNXuh05rucYqdb4vIqre4Go7POYG80
2Fr1tlajY8BoPTaz2H1rqu76jYYffqr/+uvqjz+qfvGFsqOH+bV1jJxCJiOR
QksgUjk4IgtP5JAoXBqVR6cnsFipLGYKi5HCihaw2NksTh6bncNmZDHp6Qxa
KoOSQCNyyFg6MQyPDwmLCgyNRKAi4JjIwHBsCBYXgscjSft7KRgGNYxJA8Th
Y1mEWDaByyHEcHAcdiSDEUahoghkwGxAcMQjIIhCMfsePIh6JAATAIsAA4GH
ByDCIYERsOBIWEg4JDgC6PIROAbQWtf6dmPHP9p63hkY+/bYqfunJ+fPnV99
7LGlyTNTJ458OzHy38He17vbHu+oGx/panz2mfR/vEN9/1P8l99hf7wReWMK
O/WQfP8B/tcbxC++pv3nQ8Zzr7J6jwnEbUU5TSW5bSWFrbLC9qK8joKslpzU
en5qdXJKdUJSFS+1Kja1Oi6lLi65hpegZMeXsXgKGltOYcpIAEaAIa+cEqek
cJREwOCf/4L553+h//zbwbffOvT2m4+889aja8t4gwVvtOEsNpzBgDFZMA5n
lNMDSiJZq8db7DS7i2V3cqyOGLOVY7XFW+1xZluCyZKo1TG31KQtDXlbzdjW
RG9s0mcWsL/ewEw/wC/OEzY3sFpdpMGM29zELP0fS+cBJTd1vn17R7pX03vd
3tdrg21sU2xaKIF8hAQCgUCCKSaU0DtJSKihh25sY+Ne1wX3bm/vvc2W6VXT
izQqM7Pr/a6c/znv0bkjj2a1a/30PM8tGrs2ESuiqcJEosw5rY0E5MmYIhXV
MLQ6GZN7pyFSt6ATMJQmlSBSUQQXFrJKyClRIoCFnWC6C3hGAYX0JSiOuXDn
EI5IjPtgzAviXiGm5VhplpZTIZDPgEsMPsdKcmmcj8N8AuQSkHYLPjPph1QA
RT8U+gA5ikUmAZdAn0nEbSCFouUESCK+xoHAYDthPS/qbRA1/4AnrLIsCbgg
wYcx1gdioyA6KmzjVhCZIIIj0oRdIC5pA5EhEBuDGRegUXkRoTgSRy4MshGQ
jQkY5uIwFyeyCfwSkum0lI+JszGQmAZppzifludoCR2URqclab/QRZPjtVzG
kM0oKFLCJTSX8pq5Wc1sTpdjtExKw1H6Wb740mzRpdnCmWxJLlOSzVQy6UXx
yNXR0HWp5EqWuQ4JIsNeR2d+QyMjyv4+mnwwFHkonPx9gv4d8qUp5oFY6k+R
2B/iqd+nqLto9h4uf3d25oFY7C89HSvOHDWePqw7cajk/rt1hdWlZfXFljpT
abW5rLqovK6o/IqSqsXlNYvLq5dU1lxbsfD66kU31NatqqxZVVl9bWXF8sqy
JZWlC8uLq8uNJSVqk0WpN8l1RpnBpDRbVEXF6rJSVUWpHqXF6kpjbYVlYWXR
ourC+mpzbbWpuspYVaktL1cVlyrNRQhbDDEoRgwiKdTNx3QFuA4X6wmJARUm
1eNSA8IQwVgg1s2D6nlAPQ/X/uXJfY8+vf+p54+9/GbH3z+Yevdj70efkh99
7Pv3u2NvvdH48osHnnr6h1eff+vrj27ds73ywGHd9l2KbTv0ew9oT5wxNbab
uvoMY1a13al3e4xen94TMDgclovNVR//uPKPL//+ticf+tXTf7hlza3Xr77u
6oeXLf/T0uUPLr7mwSUr/7x01aNLr39k6co/LV5+f/3SP9Quvrdiwe9La39X
jESw/m5kSisW31e+8L6KGx4p37Zbeegw3rCvYN+u+Q07RA2b57efk0Vj+kTS
SNGmNGWMx5UUbWCyZiZXEYmVhqMlaQZhWI1ITNM18WQVlamnmIVpqj6dXhJP
1gfIMo/X4vMXkuEKl6eop0M1OW5x2Cw+tzES1iUSqIwehzIc0NFpA52xBHx6
v0uRjKmphIpOKpi0POwR+6dgwI4CoITNqFIxQEdgCBExDWNuPBmAnmFiqhND
OS7lxikf4RvDPCNE2AETXoiQpEnIpeAsq0wjx5gAszSYYySziMEoyMXwXBSw
fpCcxpNeQKGGE4atIDSKRacgcomUH8amYWoKJsbx1ASIjAJfN7C3AutZrGt7
Qet6LOMU8wGMRzpIYowLxEbw2LDAIBLE0BhBjkhSTpjxwNg4CA1giQlIOwDj
IpJ2xCDGBsRcAJ0AzEbxmaSYjyBDi+cT8BItyyIYYzg6sfgk+ldZnoJsTJxw
oFQo4ZOKWV7DZ5RZWsnE5Cm/dI7XzM2ohPVQrJ5Jqdm0Ks+hJGienRGyYZ4x
MGkLFVscCVwVjyziMot4vorl6jP0Kpr+VZq9M566Lxi+PxS9laKuy3I3cdwN
GeZqoc8tdVOGXsExN/HMTXnuei6zcri38uAuxa6ton07xAd2yZovKH/+RlZV
oy2sLyqrNpXUmEurTaV15rJFhZWLSmquKKtdUla3vPSKlVVXrqqpv75qAcLw
moqK5eXlV1WUXlFeWFNmKi3RFhZqLIVqS5GmuFhbUqIrL9NXlhtqKk01VQg6
S121ZUEVAhC9NCJrWlGuQYSWligLixUmi0RnBEqDSGoQBgcJnQhqcbEOIu0T
Cwz+D0DUQFtkQecLAKK0qH3oyZ2rn9n71xePvvRWy98/HP33p/b3Pra/95+p
t//V99Jrp599ftcja9Z+8vEDzRdKzp0oR3CdOld66Gjh9l2mbTvU+w6oT53V
9fbpJiaMk9Mam0Pt9qi9Xk2Q1AVC5u6BBV9tvf2BN1bf+uSjNz9+z6rVN1/z
0LJrH158w+plv3rs6pueWH7zo8tueHjxdQ9eseKBhVfdV4sc6cJ7KlEt+H3F
gnsqF91XteiPFdc8VLVlp+bIMaxh//x9O+c1bBc1bBMd3DZ/cgR5RV2K0tKM
MZXWJpIqmtFzuaIMX05GTMhPUgKGAonJdFksWkylq+hMRTxVkkjVpdJLQpFa
t8fs9hqdTmNHk2TKanZMGXwuUyigiUXVFGUI+lQBl4JKaDKUNhHXue2SRAQZ
UQmTlHOUJB2RkA5IopjmxllKnU6KM0ki7sFjNnHCBdMBLO4k7J1CgovbcMoN
yAnc3U8ErTDhJuJOPI3kJgEucTI6SDAkPpMCcxRxKQ3QBZ+NYLkwzpOAsuFp
D6C8SLBgZAwPISGbQqqE9oD4BJGw4skxPG0F0SHo7wL2JnziFNa1saBrE571
E0j+eD8qnLKBGAqDg3h8DLGDk8NCBynlFLiLjhChfoyaBrSNyLiI6CTKmIAL
EOjAfATmYiAfQxTjfBifS0lnklIujGfDSHzxjBfmKUk2KaZ8KBVKUEKcYRU5
RslTimxKgX79XFJ1Kae4NKvJ8yoeWZQkIlE7y+su5c1zlwpzGR0bNybJurCn
Ohmp4tgSnitn6MU0dRXK8unMTdHovdHITVR6Gccuz2aX8fxijlnK0auY9Aou
szDHLpvhF8/NLM2kFowO6PdvA5vXinZvk+7ZKdm5teBwg/j8UdVtN8iNxfrC
Uq2uRK8v1ulLDMYKQ2mtuXpBee0VZfXLShdfW7l4ZfXCVdX1q2rqrquuvqay
akVl5VWVxfXl5soSQ2mJvqzUUF6GEDPWlJvrKsy1lYi+woUCgOYagT5TdSUC
U1tRpi0rUxUWKS2FSATlRrNEb4JqAUNcbkRWEwXA/5lPMdJBqRHKDYRMJxZS
oQ6X6ESEZj6uno9p73l03R+f3PyXv+158rVjz//zwusfdL7xXudr77S8+OaZ
p1/a99hz6x987LMf1t06YTc0nledPGVsaitr7Ci50F5+8oL5yEn9kePmk6f1
jc3a7h7V2Ih6yqZzuc0er97rNwfDRjJk6hpY+PlPd//hxUd/tWb1bWvu/fVT
t/36mVtuf2rVbU+u/NWaa296dPkNf156/UNLr31g8YoHFl11f93i++oW3bdg
0X11V95fe+UD1csfXLB2vfHMaezAQaxhV8G+rQX7thc0bJ1/6oDY69HEkqp0
Rk8zpmRan0xq6IyOmzFTfEmQLApFitKZUporzTDlqVRpLFKYFDpRyxPJ0nii
BIljNF7rCxQ7HMaLZ/CxYZ3HaXDbjX63NhpWpxKKRFTld8hiQVkmLWcyRtIn
C3nFdELGJFEIInhKFveLQ04YdQNhWXpGmY5CJkbE7Ej4YNor9Dp6BzB3P4gi
xziFJ+zQ0w/9wzBmgykXEXfgbBifyUAuJkZCmU8Qsyn8UhoBiOdCIEvi2RCe
cSLLh1IbRIYzNIxHRiByp8gcJp14HLE8BlNjID0OIuhjO4CjCY6fELX+IOrb
BvNByLoh7wOsB6cmQRwBOCCIZmwSD/TD2ChEqpdCkj0AkT4KpE8RKTuMWgHl
ErMexCCBrOxMjOBJjA/g+Si8lJRkI5APYRkHkRxHeMIcBYVumWkJ5SVm0so8
o+DTsiylSHnRLUU2xyvm8uoZXpWl1VxCOZPRz7K6WU47ly/M0ppMTJsMlkY8
hem4mWfMXKaISpVSVDXDLKWoG2OxVanEEjazIMsvyOcW8lxdjq3Psgt4pjbH
1OeYBTO5+hm+PuJf0Nui7WhRtjXpTv6ibLtY1NtVPdC7YHykxmlf0Hr+ygMN
V+zbfcXWjYvWfrvkw/eXvvjyoj/eV3PN8pLq2sIFSyqWXFu9ZGXNlauqrri+
buGq2gWXq+7a2sqlVSULy4vqKgrrKooWVBQvrCxehKoaVVF9dSHynwsE+oyV
FXokf6UlyKYqLEVyYRjRgkqGGNSaJEKHqlmiKYQqs1iJop9BojRIFAa52ijT
CDFTcnkPlAkMiqAGFxvveOiTu1b/996/fv/g8xtWv/Lzmjd3PvHmzsde2fr4
iz8/+tx3Dz/z8b2Pvv3hp3eMjFYMDZceO6I+eaLi3MXSs82W8y3FF1tKW7tK
2/oKW3tLL7aamloUAwPKCavKblO53Fqv3+IP6IIReTBkae688p2v/3z/Cy/f
9/I7D77+2r2vPH3Xi/fd+ewtt//1xtseX3nL6mtu/vOKmx5edsOfll7zx6VX
P3DVij8tufpPV1z38JJVD6/48LPqpguio0dEvzTgDTvwfciO7hTt3TKv9bws
HNUnUkqa0WQYcyymjEblVEbP5YtSmSJ/UE+GLEnazHCFNFOcThVFwoZY1JxO
lyWThZGoIRwxxhJVQbKs8QLedEYa9Ovc0wa/W4NwS0SkCLeQRxxwwFRczNAq
KqX2I3zCCiZFMGkix8jZhCLmIxCDCT9g03IqSdAJkA7AhANLewjEYMwObG1Y
cBiGR0DaBgPDwNNHRIQ+SRifxmiv0AOTS8G4HameJB8XIR3MIR0MElnkBoM4
4oi2QdoJEhMg2I/HRsSpaYjiGDo2bsVSw+LkCJ4ax8O9wN8GnY1w/EjBxS+x
wd1gJgBZF8b7cMaFp8dgYhAkhgikX5Ex6OnC4+OAcYL4KDoQUQypKTw9TaSm
icQkej+RsRMIXnQfyIUg68HQ3QCpIfLGWRLjPCA+LMr6Zbkk5GPoVkDEpiCf
lMwwSi5JZCkpHRCjX3yOEXpQ84wym9ZwMXmOQgyqZhgtCoYzjD4T1sZ9+qjX
wKRMHBLEtDaTLKJTpSxTQ6UXJWNXZJK1fKY0n0VVkeWESeB5tirLVs0gGLma
mWzVXLaGjRU7R5R+e2GcrKDj9Ry1hOeXZvNLczNLc7NLcvkVs3Mr5uauvjR3
zZxQq2Yv3ZzN/SaeuGto8PbN62747S0lC1eUXb2y/urr6q5cVX3FqpqF1y9A
teC6BTUrqquuqiy/srJ0UWXZFRUVS6oqFldXXFlTuqgKVeEVFYIFrao0VJQj
j6qyWBQms8Cd3iwxmKUm1DAiAKWGQrmxSG4okeoL5VqzXGMSSmtSag1KnUmh
M8u1AoyEQoeJ1cipElLzbQ+885u/vPfbJ96796n373/m/fuf++De59793TP/
vOepf/zhr2/d++Srdz7x0mOv3XXxXHHviKGrz3ywwXjsuOFMo+H0ReOZCyVn
L5outKi6Bi3D02WD44WdXaruLtnYmNJmVzrdSq/f5Cc1PlIZCmu8HtOx0ze9
9Olnq99b//j7P/7l3x/96a3n7nvlkbufvff/PXXnr9fc/uvHbr999Z23PnLH
ratvv/WxW29/4pbfrrn1nqd///cP7mxqlJ0/XXD8MP7LPuzATtHB3dj+HfMO
bccnxjXxpCKdUWZYfZrWB0lpOCyjaD2TNSbS6A5gJMO6NG1kWDNNm1IJE+nX
hEP6RMIcjxtCITUZ0IVClqEh+Yl90D2t9jtNXqeS9Agr36mENBkhfNN41Ifk
D+dZVdgnJV040kE2Jc7SshytSocIlP4SPpiJQ56Vp+NiPg5STpwSPCRGecXO
buDuFgf7QGochEeBuwcER/GUHaDwlXIgm4dEhBB6SJzifBi7lAQz6GpHACI3
GARZD2IQp+wgMQ4DPUBg0AayURCbAIkxPDEAU8N4cgSQnXiwA7ovgvGD+Jn/
FIzuI2Z8kHcC3gMY9IOGQGIAJIdBehKGhwh3B56yEhmbKDaAhbuJ9DhMI29p
F6N0mbZhrBOyDsD7RPkQ5DwIOjyHGBRuC1jOjyWHIWOH+SjOx0DGB2KTkEam
NCPnUkJvLR+VJh0QWdY5XnqJV/ApeSaizKEYSMvyGeUlXj2XMzAxZdytjXvN
wlPdGBOdQPlaRyeLOKaSTpYlI+V0soSnDTN8UT5XmuWLEYlZpiibKUL05biq
mVzF7EwVTxfzKUMuU5hFxRZl+bJcriKbq+GzNRxfw3LVLFvH8YvY7GIuexXP
L+OzV7H8sgx3dYa7ic/dnp/93UDPb1b/rura5fXX3FR/1Q11S6+vW3J93aIb
FtSvrK+9prZmRU3Vssqq5dVVy2qqV9RWLautuqrmf1QWL6qw1FWYKit0pcVK
i0VuNEqEYUSDWKMnNAakfUI/qkGgEgVDhalIYSpUGYqUOotCa1HqLSq9SaUz
/W+rQO9X6Qk5KqNMVXzng6/85uFXf/PIi3c++vydjz175+NP3/rY47c8+tit
q5/49WNP3rHmr7eteea2v96zYUtpU5uqf8jc1qVv2C89ckJ9tsV4rtF0vrHo
QrPxfKO8tVM7ajU43eWj45buHhm6sB1OtdOt8/h1waDRFzD5Q+pwWN41uPy/
P6996cuW5/57+tmPtz7+7lcP//1fD7z+4r0vPPG7Zx+/+5kn7npm9W+fW/37
5x+57/lHHn1lzd/+/vp7H77eeMHS0YKdOyU8u+zwXtGhPQWoDu4QXTwB4hFT
KqViWAPDmVBCFNbVknI6Y8hwhQmhh1MfCRspysQy5gxlTCYNpE8d9KkTMXMs
rA351X6PxjapPP8LNtypCfr1PrucdKtCHkkiTDApKenEA0i5giCTFlMppd8G
6IiET0m5lGQmo+CSklQAxpDlC8McK0c6yMaFDsaUXcCQ9hHkMHC1CnktNihB
SuRBmjWIchmgnERyEjI+YobC0ZWctMJ8AFyKooJ5P57zwhk/yHlgxobT0yAx
DP2dAoNpm+BUBVM6DOO9IDUEkwOQbBcY9Dbiw7uJE+/OmzgomUF+0g6zLsBM
4ckBcXKQSAm9NzDYK3wOPSFGDjbcDaK9GG2F6XGctoHkBKDtGGMDvBPmhJsA
5Fw474OIQSSFvBdnpiCS3ZkgzIeFwcTUNEjZsFyCyKI/RRxkExKkgFxIfImF
c7wql5ahkJhLKnKU4FFnWNVcXpdNqBMeVcKnZBL6bMZAoxAR09AJM0uVIAxT
EVMmbuJo4wxXOCvMsbHk+dIciop0UZ4rQY0ZrnhutmKGL+XTRo4ychkTxxXx
fBnHl1/uzyljuXKOr0X08dllLL+c4a6hmWvpzEqauZ7K3Eplbk8zd6WYuxLM
b9nZ+yb7/vDH31Zfvar22psXLr9x4VU3LFhy44IrVi1ccO0C5Ehrr62uua66
5tqa6qurq1YIwxnliyuLkUetLytE8bC8RFdsUZpMUp2OUGsJpUai0oqVOonK
KNYgETTJTWalyaISEmKhylSkMhQKZbSojWYVwtNgUhhNMj2SQj06RKoqVGkr
7/rzy7/583N3PPL07Y+tufXxx/5Xtzy2+lePrb5lzRO3Pfnk7c88duPTjz/+
9tKDBxRnz6s7+7VtHfqGg5pfjunPN+vONZnONloutGoa2xTNbYqBIZXDbXb5
iq2TxpFh5dS0wuVR+vzqQEgZCKJShUIyu7P0aNNTn27teO2H6Ze/a37+v8f/
+snPj777/Z/f+fShdz584B/v3f/23+9787WHXn/56X+889ZHn3zyyU9nztw0
Mkh0tBDN5/FzR/EjewuONmBH9okO7xT1tEmTSS1FqVjekGH0iThCTBYKKihK
x7LmeMLs9+hDQV06aWBpQ4bWp+LakE8VdCviYV2M1JNepWNS3HJadGY/cE2r
SY864JCFXDDiAekYQUWhb1wUtsMkCVhaEfVJwk6cRVKYJHK0NMfK2IQ46ceT
AbSTyDJyOgrYCESCRbsg48FREvR0AE8bCPUQ1AQM9GOeHmGMgHLA5ASk7HAm
AfgoHh2CvAvMhgQMkQhmPfiMD8wiizuN05MwOgD9rXh8mEDZjfeDcD9IDBLx
Hjw1gMd6AIk+vJMINuE96/ET786fPCzOuyFnE6SQtuKJPpAeRA2QmhB723Gy
F1AT4ngfQbYhJcWpcSEwplBincAy04CZBFk3YhByTpx3wazvctuDIx6RnqIz
zAkJEZ08ssdIHCX5lIQVelAh44dpN5ilJHOcGO1kQgQXl86klHxCikzpXFbN
RxVJt5IKqvi0kmcUmYQmHVUy6H8kXUjFTcmwMZPQc5Q2x5rynJnPaNE2m7Gw
lDnHFOXZolmu+FK29BJSxowhR+tyjDmHAGQsHFvEc2XC6gx2IcNeybBLGPYq
hlucYVEtYbhlDLc8wy2n2RUUc7kyyyn6miRzHZf/w5njN955Q/XKG5dcfdPC
q25csPSG+sXX19evql+wqm7hyroF19XWXicwWLO8smpJZfmSipJF5cV1pZbq
UkNZocZsUuiRkGkIuQpIlUCmIuRascqEwqDMKDCosFiUhQjDYo2pVGMpVlmK
BBiRLBrNSoNZibZGowIpps4s1RUqTVW/feQtQQQff/r2Jx+7/clHbnvyEdS4
7clHb37y4V89vfq2Zx+95bk/3fj8X2586uG/f1J26AA4fkzR2qm62K7ZsUt8
4IDuQovhQrP+zEXlhRZ1W4+us1ve1yedsmn8oUK3r3BiQj49LfP5NQFSRYYU
gYDaF9KSYQUZkg5Yl2063PD3zbF/bJh6e33Pi2s7/vbNyWe+2v/U59ue+Hj9
Ix988+h7nz77/vdvfrrp3S/P7tn7pm1CPjqo7O2QtV+EZw6Ljh8UHduPHd2L
HdoumhhWUpQxw2pYXkdnNLGoyu+Vkj4JndIzjCkeN3ndmqBPQyX1bEafodWp
mDrglPps4qhPG/WrfFNEbxu+b+P89uNEyKMIuqSIwbALRHyQSYCIC/cM4lGH
OB3BM0gZp6EQAFM4h9IcI8lS4kyUQGpIR2AuI2GRFEaRCGJpdEm7BCcZ7BM7
mzGyA6SGicgQ7mrDIyMA0ZeaFNSHR8qSAuEhhANA2jcbxrM+BAKOAJwNAH4C
UFYQ7Yf+FpTpxBk7YD2Q7MJjfUSsC08P4NFOEOkgIl2APA9bvyw4+QFikJjx
Am4acDZAjcJEL04P4AyS8lGJq1kURZo4CiOdiFw8NUSkxxB6MDaCo/sD4pSb
gjmPgCHnQPcEIutFbUEZUyjPjgjiiDJmxilIasZF5FNiNoJzIZwPCSOGubgw
vJJPiC/PeYO5pJSLSpAgznGqbFyWcspTPiWXkvO0KpNQURElQ2lZykDFdamw
JhPXc2l1ntXlWB2f0eRZI0+buJQuSwlTbmb5orlcySxvQXFyhhXm4fAsypJm
LlPCZyo5upKlq1imgmMrEIw8V8VnkRoKvpQXtlUsi1SyhmXqWeZKJnMlTS2m
qOWZ9K8SyXvferF+5corr71p4TLkSFctuHJVbf31tQuvr120akE9yobX1go6
eFVFxeLy8kVlpQtKi6qLTZVFuhKLymiUafVipQZKlbhYjomVQKohlMiUGqQG
o9xkUloQp8Vqk0UY4ygsVplLVKZSpalYjjyqEZUgkQoTAtYo+FVL9e8e/ftv
H3/5/6356x1//csdTz98x1No++jtz6y+/W+P3v78Y795cc2vX159+0urb355
zb2v/nrDeunu7cSBg8qLLQhD447t4r27VBdbdI0dinNNqvNNmu5BVf+gcqBf
Zp2Qe4PmQLjU6dY7XMoAqSbDSAQNgYgyGEZBDL0EDqf+dPtz/z3Y8c7W6D+3
2N/aPPHGxr7X1l946fsTz31z6Nmv9r7w1Z43vj7w9tq277fumxirdEzKxwfk
g11E+3n89OH5Jw9ixxsKju4qONWA+72qDKtlOT3LGVJpdSgo97vEQbckmVCn
KV0sZvG6tQGPgk5quYxOGFgPqwPTEvc4TjpkEafCOlhwbI/4wI8FjhF5yC0L
OmDMS4QcBHKhVBB4+4F/SBxzizJJGHIRgUksgy6/OCbMaaGFNXdUgMiECD4h
ytMSOiTiQjA5iTM2yKDPGYGeZjzQAuJ9MDVKeFtBsAdSUxDpTmIUyziRFBLx
CVG8X5xzEZeCIOcFQsMD5wKQR4o5hkd7CX8TUiIx8ooo4gVa8UgnEe+EqR4Q
acNjnTDRDTxHYOvn8099ON96AOYRODaCn4Y0oqwHZgYBYjA2QHiasVi/OD4A
Qm0g3AaRlU2PIZ0Vx4ewjFVMjaGjYM6FczaMdxLIyqLiEPWT4mgXElYcIYkC
Y2pSiJD5sJSJYmxQlCNh2o7xfuJSWjKTwi/PeSP4qIQLAySIc4wiG5cknUTa
q2RjCo6S0TEFHVZzSS2b0aXjqnRYlYkquaRyhtHMMOospZhh9dm0jo1r+JR6
JqOb5RCDyJ0i+dOgl0gEeUQfXchSxZerkKcvp0KuJMuV8mwxz6FCL8tyfEWW
E9ZPcVwFh4SSqWDoiky6kk7XUFQdlVrKZm8+sOPqG66vX3Vz/YobF1y1qnbJ
yppFK6sWrqpaeH3NgpXVNddUVC2vrFhSXnZlWdnC0pK6YktloanUrDUblUaD
TKsTK9WEVAXESpxQ4hIlIVfLNAa53qg0m5VCN2mR3GySWQxSs1mMoqLaJFaZ
ocoChC1qmwhlIVCYCXWRTFd5z+Ov/O7JF+7665o7n3rkjqceuuOpP/8/lMue
f/qeF1+455UXH3jj9QfefutPb7304Fuv3f/KS29+sOzn9WDrZmLfHunZc8qm
dv3eveK9e2SNLdrWLk1Tm/pis7y7TzM6ikphnVQ5vbpApNAbLPIJDKojYUMo
ogqGtMGILhDUB0lZMIgNW5fsOLXug+1jf9/ieGvrxNube17f3PLqxqZX1l94
Zf3ZN9edeXtTywebB3r6fu31iJ1TsolByWAnaDwpOnVIYPD4XtEv20VNp0Ay
oUepkOPNDGtMxOVBj9g7RQScklRcF4+rYlF9wK0lPSoK2R5ay6aU6YgiYCOc
ozBgl6Cg131OtPPb+V0n5KRTQjrFURdIIkdqB1QID00CRxdOjkuSfpCKEN4x
YVoXh2xYBMykYS4N2DCeCeJcBJ+hpHSIYEmCRlHOSrA2kLbiwXbobwRIs+hR
gAQx0AHTVoD+KTUGqEmYj0LKiYU7pNw0MetHSgRzDuKSm5jzwyxicBSP9MBA
syCj6BBqAg80i8OtINlBJDtBFDW6IWpM7cDavyw4/VHB4A7hcN4m5qdAZgBk
egA7jDOTMNyNB1pRihTHuvEgOpl2MWIQZcPkKIgjFR7BmTGQdcCsA6khjhq8
4/LWRiT7AD2CIx55t2CM0TlzXvSLizNunAtAJIsZBzEXh7NJMRtEphRD9x+k
g9m4eJaSziblafRndCDFFGa6ZmJyOiJlE0r098/ElFRIQYfkXEySp+UztDKb
QvlRnU1r2LiKT2pnMtpZVnuJM1zijLm0JptCVKLScSktl9YjoeQZExJEnjVz
QqMIAYhIzPFlWZQZUU5E8RApIFPDsrUsW88wixh2MUUvo+nrUtTKZPp6hr2j
+fSvrr++esV1tYuvqV20vKp+WWX1srLKq0rLl5WUoVpSWnJFedGiksKFxYW1
AoDGMovWYlTqEYB6iVJLyDVQosaAej6mnI/LC8RKiHaqdUCtx9UGqDXIdRa9
wVRaZlx4pXnlSuNvfmP6432WRx6yPLWm+LmnSp96svTR1UV/vL/krjtLf//k
q7976m93P/3kb59e8/tnn7nvhRceeu2N1W+898Tbn6/5xxd//ddXz77/w9/e
//aF99f+7V/fPPvOvz76dNHa7+et+x5s3iDev198sV196Ihm5w7i7Gl5Z4+6
s0vV3q7s6JSOjqkmp9WTUwqHUxEImoKhokDIREa0kZg2EtWRETUZ0QRDGj+p
JEnC41W19t218ejP/9o2+dZm61ubu97Y3Pr6pubXNp557afTr286+8pPbTtO
/DPglXtdSvukZGoY9LehYFhwEjnSvfixPdihbfMHOsVU2shwWuRIWU6TSMhJ
j9Q9Cb12Ih6SR0lZOIikUOO1yxMhFUupmJScisrCDolzGPONS1xj+Jl92K6v
seluGLWLww6Q9MK4E485ibgXuvuhs1OYIM3EJVE34R0FaR/BkCjNwXwa42Mw
48fZAJGNQT4uTnkA6wPJEchOAWYamUnc3wwj7ZAeBPFe3NuCxwYg0qbMOEyP
g6wXcgGAEh8zAnNOpGIwZ4ezKF4hUzoOKWSDu2CwBTGIVEkY6fNeJMjzWKIT
j7WBeBvI9MLweTD2M9b1jejUR/O7N4IZO8jaJfwkEFxoP+BGBV8aaEX+U4zy
Y6QdBC6AeA9AeTAzAaJ96DxxegjnrEQWwTuF1BDP2vCcDcEIqEGY6scFVXVC
1oalxkTUFMEHCdotzMBhXYI9ngkRsyjVBkWMB7IBiLwoHxXnEsRMnKCcRMoJ
OBLFRiITlWTCUi6tZNOKTEyW9svosIxDgZGS52kZn5LkKRUfV3FRLRfX5ijd
DC0wOMvq8kl1NqbmYyo+ocxejpNZRsczei6jRxhmWQsvFNI+lA1LeEH1qjlk
Prk6jl/IZlFdiRIiyy1muCWX19Rck0yvSiRvSaTu7uu89dW/LXnhqaXPP7Xs
6TXLHnvsqtWPXfXIo0sfeGjxXb+tu/lXFcuuLqlbaCmtKSyqtpRWGcsqDCWl
+pISg9mi0+o1Wq3KaFAX6lSFemVJoaakVFO3wLx0afF11xbd92DRux/Urfvx
ir27q0+frm1vqevtrBkarB8aWjg4vGx47JrxiRXj1hXDI8ubW5bv2b3ovmdf
/8Ozz9/73LP3Pf/Cgy++tvq1d596+6sX39382kd7Xv/Prjc+3v32Zw3/+GL/
P79o+OdnDW//p+GdD77+5POq776Z982X4Puv4I7tWGOb+uhp1Y4d8tMn5f29
sv4+RW8vKun4uGbaobY7FU6XQhitC1eGo6XhuC6cMIRj+lBEG4pqEZWBoMrv
V/gDhMOuPtex+qv9Z974eezNTZ1vbGx9deO5l346+vLGX17YcPadnw9NjC8N
+OUeN3COg8lB2HZedPowdqwBO7YbO7Kj4JedBdYhRYbScbyRzSIS9am4CtlR
1zjwTuIRv/DYpVBQEXTrvDZZPKxkKTmTktARMTkldvQA1yA+2obv/nLe6Z+k
QStB2vGwE6QDIDKNJVx4eIKwteLubizuhMh8uodgyCqsTaD9ICtMqgQsCWkv
zpKCMqY9MOMRFBAlMnaKSA4DBFG4BVIDID0A/C14qItIj0JmHJGFrm2QJ0Gg
HUv1wuwUyDthdhogBmd8WBYJZR8ebsXJJuGjkFcMdeKes9B/Bk+0wVgzSHdB
ugd4DoisW0DX9wUnP5rXsRbkp3BBCidhZgBnBwA/DphJ3NuEk61ETJBUPNgM
kr0wPYhfNrogPQToIZCdJNDPRQk0Z4P8FMZZMdYKk90Yb5Vw0xDhT4/h6VGc
9wmTSynkip3i9ISI9+KzUcgHMdaNbjsE6xNlQ3gujM+EQcaBpaYxpIlsWJwh
pXRYzKdkbEpBR2QZUsaEpXxCOisoIAKQyNFKPq5gYzIEWp4y5CltntHPMvpc
TMZFZChR5lKKPKXJZTQoMCIZRYGCR9mQM3NIB1kLh4woX8EJj6lZxGcX8/wV
HL+IYepoqiadrEzEy+Oxymi4OkzWkIEFZGAhGVgaCNaToStjkWuikWti0VWR
6A2h8A2h0A0keaPff5PTdf3ExLVDg8u725Y0n7+y8cLi9uYr25sXtrcs7Git
b29e0HJuQevFus7WmvbmmpbmupZm9J6lzU3LW9tWtLdd29u7eHikZnykanK8
etxaOzC8oH+ovn9waXff1V091/b0LG/pWLFzR93LL1lW3WysqjX+8fnXH3jh
tYdeenv1q+898dp/nn37h1f/teuf/zn5/hdNH37Z+PFXjZ992/z5962ff9f6
+beNn3x94qPPL372+Xfffq9bu1b0zX+Jrz/Fd2wDF1tLT14w79tLNJ6X9fcq
hwaUQ4OKoUGldULpcGldbpPTpfUGlGTYLMznTJhCMUMoqgsJgojY1AZIhccv
8XuVfh8cH684cv7ZL/buf33ThZd/bH1p3ZmXNhx68af9z/549PCFJ8NRScCr
cE/jjnHRaC+4eLLg+EEU5URHd4oObRcd2YVNjyopWsfyBi6r5XldIiL32aBz
BEMyR7qlpEcc9mmCHrXHBuOkgkkp2CSRDoHQJO7sFk13wKZ9ol0figZOEzEX
JB0g4sKQqMWm8LgdevvhdBMWGAIMKU57xa5unHLBjA9yQSIfQ3d7dBFCxovn
Y3g2IklMY0gjEoOQsRKZURhqRxxBqhfPXI5jgTaYGCKEq3oYZsbxGT8R6cGj
zZAbg0iAshPwkgte8mP8KI4CXbgZoGIEBqUIVdcJ4D8F440w0YysJky2Eo49
oskdoPvH+UgHO74BOSuRQ+ozAZk+jB+EuUlIj0HvBfRzYbST8F3AUYpMdMHM
EEgOCik13QcYxCASOCuWnYIIRm5MxFsF1aYHITcu9PAgilPDGGsnWC+ensTY
aWGAg5nGZ0giiwyAE2c9YsaL8UE8G8TzAZx1iFITImRWGRKnA8ioS7i4lEsI
q5KpoDCan40TM2kJ8qu5pDiflnGItaicT0hyKBIKC4RVs6w6lxLnkcsVJocr
EKRZJJS0hqeRAuo4xsixhYLwXR6b4LN1fHYhw9RTVG0SERctiYYsEdIcIYvD
gWLSXxL0lZB+1CgNBsqDwQoyUE0GK0KhylCkhAwXhyJloWh5OFoeilaEIlXh
cHkoXBKOlEXD5RFhfxkZqQkEFvp99T7vQo9nkcez2OlaMjW9eGz8ysGhK/oH
rujtq+3urerqre7urejuqegdLB0aMQ8Olfb2V3f21Hd0L+3uXdLZe0VHT11z
a/Xu3VV/e8ZSU6UGEu08WIhLTQ8+/8bDL77z+BufP/uPtS/9a+ub7x169z/n
Pvmi57/fWr9bO7F23eSPG6Y2bHJs2GRfv3H6h3Vj3/7Q/d03k99+/e7a7yXr
1hV89zX8+guw+Sfi3Hnz2UbLL0dkF84r+/rkw0Oy4WHl8LDKOqGxIwD9Rq8f
YagWMIyXheOFoYQhEteHL8NIhoWvb/B6lR6f2udXeNyyofGyY413f7P703/8
tOOVH088v+7Es2uPvL/tG6+rKEzK/F6Za1LkHIO9LeDk0YJjDfOP7hId2Sk6
uK3g8B7MblVxnIbLabJ5HcfpIiThnRZWLriRHtlkATsMeaWkW+WdEr61IROX
sAkJRRKRSbGjGx8+h51YJ2r4ROTsFsfcIGQj4i48PiWOT+OhcdzRAj3t4pgV
ZqOAHMN9vQSNDJgXoJs/T+Ic4tEDeT+ObFjKDlNTIN4PaKR0ozDWBchGIt2N
MhoebkPWFI/2EPQoRHjSI6IcCq2jOHkeMAiZKcGCzjrAnB/nhvFUJwyh+NYG
2RGYscpzNlPogsR/AsTOY6kWIe7FmyT2vaKp3VjvhvnnPi5o+wLww8SMC+et
BNOH80NwZloYRvScF/phkBb7zmDxThDvItCJxbphvBukunF+nEAKyI/hAolj
iEGMGSXQfm4cshMidgpSY2J6Auc8QOgUnQD0OKTHQQ7ZZi9k7bgwuI9CYhAK
APoJ1gFSkxjnRQlRRPkBjZIysugJYXIs5SNov4SLiGdSkpm0QGI+gZROjADM
xuW5lJxPCSP7lzKa2aQUvSeXluaT8mxSIbhQpJUZFc8YeOH7AkqyfDXL1DKZ
WpquS8UroiRCzBwOGiOkPhIyRMOWSMgYJg1kwBjwm4O+YlRkoDgctIRDRaGw
JRQ2hUNlobDxcrskFKkMRur8wSqfvzwQKA34SvzekoC31Oet8LgrnY4K21Sl
daJ6bKxuaHhh/8DCnt4F3T11Xd21XT3Vnb1VnT01nV1oT+XAQMnQYMXgYGlv
X3lXd1Vnd01vf03/YE1nf3VrR/HRw5ZXnzMsqFHhQD4PqERSDZBpocLw2Guf
rXnjm+f/ufmNjw6+8/HJDz9r++LL8e+/9274KbplS3rr1sSO7eldO+hdO6id
O1Lbt0a3/Oz7eaPv5w2BH7/9+Pvv8Z83SX/4Hn71acG6b/GjR7QXW0xHDivP
nVH09EhHxhCDyrFxlApVNqfS4zcESKMvoPKHkAstiiRLIgljOKaLIAwj+kBI
HQyp/AG52yvz+FQer8Jul/QPKE6cLlu/44531v/jhR8a1nxz7GTj3Yk4QQal
Aa+Q9aZHxG3n8VNHLw8Xbsd+2T7v4Bb88A7M71LxWR2f0/I5PcfrklGp3y4s
4nP0Qc8o9E3gIac44lO5rIR/Snj0NBMXFsxGpwlbB959GD/0OXbmR1HcLona
8CiSMzsRm8Djk0Swn7BfAIFuYYSaI2WODjzQj7NugveKsujm7wUIQ96HZ5EB
I2F0lIj1wXgXQEEv3Q9CTSDVRTCDgqj5m0CoFQkNogwyI0hWhAvbe1Igjh/D
+DGIMt2cV0hzqTYifB6Ldwg61f4D0bbO0Pi1IngOj14A6TbAIAZbgXMfNr0X
698kavysoOk/GNUD5txITAFiMDsKZm0g2gG8Z5GnhcGLePAsHu/CU32IfQLt
T3QQdC9iEMVGhK0gwdwI5EfEyS4MiSCPXk5h9Bgh9Jq6iPQEioQEcsXUCM7b
UXol2GkceWlOmF0jTBHP+yFjQ0IJOL8kg+jz4XQQcDGCj0mTXiLlQe6dYENg
JiEIHB8F+biMDRFchMglZTmBNVk+rbyUUc/ExbkocvgoV6L9CEApT6myGZT+
SrLCs9rKqXhJMmyJkyZU0aAhGtBFSW0kpIuiCmoiqE2agj6T32sM+hGGhlBI
R4bUJKkjSQNC0u8v9PuLkSYGfFV+X7XXW+3xoCpzu4v8HnQgekORz1vscZdO
TVVPTNSPjNQNDNb091f391UODFX1D5X3D5T39VX09Vd195Z29ZT19pT395cP
DJf39JV1dpV2dpX19ZcPDhsHh3TdPeoLzcpz5/SHD6ruv0sM58nmzUPyJxUh
BgkVLlaLJPoX/rHj1X83vPXBsX9/cv7Dzy9+/uXwt9/6Nm6gt2+d2b1rbu/u
S/v3XDq4d+7AXrSd3beL3bMttWtrfMeW+M6fQ+u+fe3HH+DWLZL16+C3X+Dr
fyBOndE2tuqPXsawvx+JoGpiQj45qbE5tHanyuPX+MNaD6kKCBjqo3FLBFXM
KMTDqC4Y1gRD6kBQ6fFInS6p06Gamlb092HnT87bvQP/9MeFr3350g/bnw+H
tOEwEQ7KvQ7gngJjvVjzaezUYfzobtEv2+b9sg1r2ATOHIQRUpnLKnJZfTar
5jlNOq4I2nFHn8jWBd0DhH8chF2ymF/psuIISeExL3FABYRVQhNNootbsL3v
i4aPSlMOPDJVELcRsUkQGwexMamnBTov4tEhCXKe8SncdhHGR8TCiLYL8m7I
enDOC/gAlo/giQkY6yfCbRjVB+gBEG3BUh0wOygNnRO6SQPNokQfYIcIdhjP
CJENuo/hsWYxOwS4EZCfBnMeQCPBQkYUSV6HeM4Nz3wmu7tK/PodsuApIo4S
YjvG9cFEG+5owGx7saGfRRc/Kej9SZ6d1s66xPkJQQdzY/isHZJNmOcUHmqC
/tOiSCOR6ARUPwqnRKwNoMPZQYJHRncUz42D7BhqYFSXNC2AifNTkJ1E0RXj
HBg9Kcx8o8ex9CCKjcgYA2YKQx6VRSnSSXBOPO8BSDHT4xiH/g4+mHZBGoEZ
BWxYknRKEg6IqGQvT0BFxYeRY0d3qsuDiXFJPolCnyRLyVBCzAvzw/EseltC
nE1J+bSCyxjYtCWTKE9FyuIBY9ijCbs10YAmEdYnIvooqY4GFTG0JbXhoC4S
0IZ8moBb43drSb8qRGpCpJYMaPxejdetdzqNTmeR213u9ZW73SVep9nnMnjd
ar9HFURH+QqFb96xF09Pl1vHS0eGK4aHK4dHyoeHi0ZGLWMjlqFBc3+/uW+g
uHugtLuvuKe7sK+/uH+kqkfwnBUdXeUdnUW9vYbhAd3ogLqvS9N4QXH6pO70
GeWm9dJ7fy2FUDoPUxSIFPNE8nm4tAAqMbGqQKL65wdn/vXRufc/af7ki67P
v+j/5mv7T+uSO7bM7ts5d3Df3MGGucMNc0f3zx3ZLzT2787u257ZszW5a0ts
95bIri3etd/8ZcOG+Tt3SX/aAL77Bt+xVXb2vLaty3L8uOL8WUVvr3JqWjtt
005Nqx1uncOjdgd0gagpcBm3cMQYiZovL11HZSAjWjIiqGEwqPT6ZA6nzD4p
HhuXtHbiRw7P3/nTvB++m//115bJMX08rgyR4nBA4rPhnikw0IGhYHjiAMqD
ogNb5x3YNn/Xxnmn98vjpHZmRpXLabNZVZZX0UlpwIbZ+3BbJ3D1C4/lDDth
MqhAaugexeIewMQA5cfIEXz4tOjIlwX73i1wt8niU0RsmkjaYGwMj4/C8AB0
XcT8reKUFeTCEl83dDWi65Pg7cIMMdYOeDeR9YnypDBGH+kBSH3ibTjdAxPt
eLIdZIcI8hTwHscDjaJwO2QGJNwwhqIZNwkQg8EzRKaX4AaI/ASYcxLpFjx2
HkTPQaoLzDmI0f2ym4qwexfC8e2QbsfpDhT3JOl+qb2hwN4gGtsqavmswH1K
PheuuuTV5REdA3jeis/YYPAc5j6OB88B3wks1kwku0BmECQ7YawJT3Vg2RF0
DjA7hoIkzo8icokkonuU4Kw4h2znGGSmhWlsCWEIg0gPiJCs85MEa8UZK85O
AlTcNJ51iJlJQI0WsA6UGSHtxNNuoYeKCxNJJwrUIOMRswFh9VMuLCwM4UmC
RRIZxPkIkY2K+Sgxk5KjQmBmEZ4xwCOhTEq5lCqT0CVDhRGfNuxVRPyKiA/9
t6oTYQ3aRgPqiE8RDahiQZXQ9mtIRJNDE3Aqgh550Kvwu+U+l9LtVLsdBrfd
7LKZnHaL26H3ODQ+l9bv0QZ8hoDP4nUXuZ2l01Olk9aK8fEq61jFpLV0wmqx
jpsnxvUT41rrqH5suHCw39LfZ+npMff0FXf1FXf3F/UNlfYNIsNZ2tFR2Nll
6uvTDgzIhockg72Slgvy00e158+qz5xU//sNWV2dHEDlPLFyHkHMxySXGZQU
AJmIUM6XqD78tOOjT9s//bz7q6/Gv//Wvf6H6JaN2d3b5vbvmju0d+6XvQJ6
Rw7MHTk4d3j/3ME9uX3b6b1bE3u2xPZuCe3Zktiz2fvD13etWzdv2w7Jxo2S
jevEu7fLT55SN7Ubjh2THT8m6WxXTE6pbXat3aFz+PTOgMEdMPjDejJ6Gbqo
LhwVlvtF4iXhmFnYE0YYqv1IDX0qm0s6bhUP9MILF0V79mI/b8DWfT3v7DEi
FtWEwuJISBryCs8xc4zjPS2ic8dFx/aLftkh2r+5YN82bPeGghO7gGdSO5M3
zszosll5lhO+qTbshs5+zN4hdvRA7yAWETpnpL5J4BrAwnaQCeEpFwwMYT0H
8J3vzj/8sSTQR8SnRFGrOD5BxEZAdAgjuwj3BTzUBRmkfQHgahbaSAL4aYKb
QroA814UlIicH5BdONksJs8KCphoI5Cx5PqxeAu07RU8YbARprsgNyjEQHYc
dx/FXQewRCOgOsX8CJydFieQ4J4BkbME3YPPTkHyAvzbKvzOCqJvozbXhSWb
xdFmImsz+05B5z7RxI6Cnu+wY++KOzbUta0vzk9JsoPY7ASRnwK+k5j7KPCc
wHyC1MJ0h9BlGhMAL2B6ITdEoMqNw9w4whYmWghmQPClQqIcE+bYcHaQHIbp
ISLVD5ghMRJBBoE5Clm0tQrjL1kbkRmHqVGAjCjjAmkHpJzCQ6IyARypYWIK
zzgh5yOEwEhCPghQsSjtopfIiIYAFwH5hDQfk/ABnAtgXFTCRsR0SJEMKONe
VdSjiXhUUZ8SmZaoXy58rXAQNRRhnzzslUf9yojwPYxK0iMPuGSkW0m65QG3
LOBS+Jxqr1PtsevcNoPLYXQJGOo8DrXXbfb9X9CrcDoqbVPlk9byCWvF9GS5
barMNlVsn7bYJk3TE4bpSePkuGl8xDgybBwYMPf1mfr7Lb29iMHC7v6S7v7S
ju7iji5En7G3RzXYJx3tk/Z3gs4m2YWz8jNn1U2NmoP7FU+slhmMGqjQSZQa
QqbCgHIejsKgZD4uKwAKjFAiR/r5F4NfftH/9Zcja7/1/rQ2sml9euvPuZ1b
Z/btvHRgN4LuMoP7544eELaH9uQbtmf2bUvv2xrfszWEMNy/LbFvi+3r//76
22/mb95M/LSe2LQObtsED+yXXmg1nTyp3r8bbzqPIqHB7kRSqHb5jR7S5Anq
/g/DqI6MIflDJBZH4yXRGArIOkEKQ2qUHJ1uuc2mGBkWt7RgRw5hO7YVbFwn
2rWpwOtUxmKycEgSJaVBFx6wg6lhov0idu4YONaAHRLW2mP7thTsWldwYP38
sQ4VnzHPzujylzHkMtI0iXkGRPZ23NEO3X14GBmtsCxsJ2w9GDkhpv0SdA/3
dBFNW0Xb35z/y8dYZEASHwHhYQxJYWwQFRFsA75GPDFA5AI4bZe4zouSA9IM
um6nAYOylU0sDLX7QHQQ957HfSdg5KIo2YYlu8SZKSk3KbYdwFyHUEbDoi2Q
7kMUwMwQ5j2BWbdh/uMgeh7LdCNPSIRPiULH8dApnO4VUIo3gh+fLPh1kah/
m5nvx1PtYHQrOP2ZbrRB4zlYML1XNLYB+/AO/Lel+IvXSulB3cwodmlCkp2E
nqOYAPgRIDDYhNHdMNVOIN9LDcvZESR8WA65Xys6DTzdCtKdgB+XcOOARQ7Z
inHTksQglhqAgqNGrnVcwo7CzDBAW2YUcFaCt0JqEEsM/t+8oNQURtkB6yUo
D46cfAIp6fTlmW8+MecD2YAYeXXWBwQAkQ6SWDYKhQX7IYLx4KxfTHslKbc0
7lREHLKYSx73KGIe2eUvW5TG/PKoTxZ2i0Nu4XvfEIaoQm50AUgRgEGEnlPu
s8l8NqXPrvE5DF67EdHntqs9DpXbrnTb9S5nudNd63LX2u3V09O1E1aU9RB6
ZbbJoulJiwOppMPosBttNkSfHjE4Oa6zjhpGB42Dfcb+fkP/gHFgsKgPudD+
kvYeU3unsbtL19+rGOgRo+rvlHScI84cl5w8rWlu0jY1yb78RLbqaplCq5cb
zAq9XqrSihVqIFaIgLwAykVQoA95URwqv/5i9NuvJn742rb+++DGH2Mb18U2
/5TY/nNm99Zsw47ZA7svHdp7SWDwoIDhL3tnDuzkGrbTDdvT+7bH9m0N79sS
PrgjtX/b1Def3/nVl/M2rIc/rQWb1oKNa7HdO4kz53TolPbulFw4o7JO6hwu
jdurc/vUvpDBEzJ4Q9qggKExFBNGDMMxQyRWFIkXhyI6IRiSSp9fbp+WWcfF
fb3w9HGwe8f8LZtFm9cV9LZIYxF1LCSOkpJokAg4MK9NPNIDWs/i547hJxpE
B7aIGn4u2LOpYPd6UcP3BRcaiJBTP5czz+Y1PCvjaVk6IPYgNWyT2FqhsKzP
jtFRGHETti4QHLu8Vn0aTF/Az/84f8sL+MUfCGZSkhiGkQEsNghjaNuPAh0R
bAEZq+RSCET6cPd5QI8ih0aw45AeBTkHIeQjlFjPYZ4TYv8xLNosGd4njlw0
5ieU8Q5sYqfgSMlz4lQH4IcgM4gFzoimfpGy44WJRkWqBeeGAXlc5N2PB47g
4YuiVA/0HMLPfEC8dJNu6lAZSoL5Qcn+t1V3GrGdr+HBUyLbHjC1QfTTauzG
kvlrFhPBRs2lqYI5G+CQwh7CPb8g6nH/CTzaBOgeLH4R+k7jrNU8M63k+sUI
wNwYQaF42IijiCp0h1ohPSaMSqQGQKIHpPpAug99FGBGsMwwZEdQA+fGIDrJ
ZDeGgi01Lvjw9ASRmhQeUIMqbcPjViyNLLEDz7oJYSGGV8y5AYsafsj5BUEU
lgNHEZXIu2LCVPBpIjoljtklCbc84ZMlfNLLT/6XxLwyVGEX+k8UKuqRR93o
pYR0SkmXLOCU+abEvikpos/v0HuR2Nk0Hrvahxp2LaLPYdfb7ZV2e63NVjsx
UW21llrHiyasRVMCemb7lNFh0ws1rbVNaVB0QnoxMa6bHNePj2qHh7RDg4bB
wUJE38BgeV9/CfKcHZ367m5VX49yoIcY6MYGOkDHRfGF48Tp44qmi7quXsXR
Y+o1q1UlFWqZxaS2WNSX53hL1TqxXA0lSgxeZlCY4aYWGJSov/3S9v3XtnXf
eZAIblwX3fhjcPO60NaNyZ1bkN5l9+/K/YIYbJg7dmDu2ME51Di4O7d/J7d/
ByOQuC26b2tw/7bU4Z35/Tumvvriri8+n/fjd/imH8GmdfiPX4s2rcOO/KI6
fly7fTtx7LB8ZMTg8mi8fp07oPGFBSn0hw3BiCkUM4bjCENjWHgMRRGypqGI
6f8T9R5QUlVp2zZV5+y9z6nQOTexaWKTEZFRRCf5vjoqo+MYRp1hTICiEsyo
CCgZOuecq3Omc+6qrpyrukJ3dajY1TmBaebbB7/v/9d61lkNvRpYVF113/fe
z34240jtvLERH4uJVithdxeorgB5OaysFHZVARwf9ZvxcjwO5MXB0M6M2B3W
Q1kv0dtKdNSzG0vZFdmEIJtdnMYSJBOlceyKBLa60/eXhdX//dXv53s4/qN5
B7JjNeyF1l6MIfKa0ZIHua3QLCTsOC5ZqSk9NN6FzbHs7FPsnhRqcYiL7ZZX
ypz6mZIjr4Se6ARTIurHEZwB0Ug72z3AXdGBFS3FLHgawM8j1E+jyNFPWmuh
rZL09KCqCz43XwkwVfN/tUFrFWkrA/a7TCi7p8RvZuTqgupC3rImfE4YPNNF
4lToqoWWXHKkFNgbyIlawlxEWDLRYHKQo5k/JQb3NHTWcf7ttyJNtZHOWral
hK1JYtedIV+Jhsd2UxNd/P9awS96akVFYIs7XknayknnXTjdQy0MIG8XkKbB
vji/ZUXQPSX/VxO9JAaz7XBhAFvQBwDq4RIGSgW9QnJeQs9J8V/HLB8tq0jM
3X0t+lELV5RoRghmZIBxoWZ6wQDnDMz0jIVhNG9Gs1qmGW+ZOcGBsJtl1m2G
0coI03Z+bxxgAJmJGS5qeZie1aEpPfDowOQQnLFRcxO86TE0NYqLmhnlzNi4
nmGEkzsur43jGea4rbTHSrustMNC2c0cu5lvt/g7hgMnRjB6fqNm/pjFZ2yY
PzrsOzIcPGJdb7VsMQ1t0utW6zQhBk2wQRuk1wWYDAHWIX8MndUSgJ8Wc6jZ
iKOf/5ARfzdQrw3Qa/y06gClEmtfBAOgKlIiDReJAsSDPjKJj1zMl4uRSoQk
XZzORqq1notVRigO6u/zib/JPXLEH6PnuyY0YE14UHiEXxjDIM8/iOPjj7j/
l0FI+SFOANPszQ+KvzWceGckJcGenux9wKAjM8Wdkz5dkDlfmnevrPBeVcmv
dWUMgExhKSz5pbL4x/LC++X5K+X5M2W57op8O5bC6qIlQe5w3PXnr31PJN4m
MpNQZhKZfJOddIMoyKHKy30K83hlRVA0wBu2+WMMJ5zBE55AzOCDCnRNhXum
IyZxNpwMdU+GYwY93nCXO2hi3Nc2zDMZuNJB0NoEyovZBZmsnESitw1Me7lT
bq4La5aL6xmjJizQrEayPiDsAF2N5N0yVJ2HBZFdks4WJJOCeHbpTXZHPseu
C/nvStivK7yfFqglN3Rr4UgfsHahMSFn0oDzIJoa4Q0PkqODaGYITmnRUDO8
e5vM/oDdeYfySqkFLZiSIq+YmpahSSF0dpBzMvrncbBopEfb0LSYkYklFVhU
kD+bOVgN5zXQXE1YisFsN7r2GtrEZeee4f13As3K4VAhOVYH3K3kggjcV1NY
UMrOUNf+4ZP4tp+nFS0OQnsNUCcSmhTCVgpGy4A5jxzJJEYK8C+p0XJqtgWU
vE/VXQ1akIeZi2lHNWnOh+o4+uwRdGwvx9vrszxALg6AZRnCPzteAcYrgbsZ
zWOx64BznXT6W9TxR5Gh3O8XrHeYpnZyvgvdV9P402NZTy1hmjTIMwBmRdT8
IFxWMJ8Syypm5wLTh/+1OEhO9ZMzEnpey/SfLxjhPCYXf2FmDv7P6OCchkmL
D/b34coQYp5WeG+E2UJlGGR29pl9xikp9EgptwZMYmzHOLMT3GkbM9N4ZpSa
GkY4rXtx2Sgvc98ihfOCywxdZvyk7CZMH89h4TssPnar37jFd8zMG7Pg8rFZ
/G3DYcPWSLNprcmwGvtJvdpPr/bVqX20aj+tyteg9RvS+Jp0PqYhf5MxYMgQ
aDaFmodCDMzySwCWP70uWKcJ1qpDVapwpSJSIcdhMFAi8ZNh5ynlygcpWR8l
7qJ679Jt9bzWZn5vT0B/v192Ov+Vv/FXrw/1CQsNiAoLXrs2eHWof2Sob0go
PzCI6xuAGaS4voDikxQfcvwQz5/iB1A+gfGxtuS48ZQ4e1qiKz3JlZ7swJWd
NlmQMVOSiz3nvarin2sfMNhY80AKBf+pLvkZY1hZuFyRP1ue5ynPm6wsmK4s
mKkomBTkOJPvfHPlEhV3Y1V6AsxKBukJrPhrROodsiifKi3kFmSilrucIZPf
2ESgwxPkmAx0YOfpDXW4gxyeYM9k+CSOhN5glyfE42Fk0eUJm5gIGbH6G9SU
qI9orCFK84i8NLI4lTRrfeZn+JNOyjMBZj08NxYdK7JooLwPDnag/rugvQrU
FbKrconSdFZpCsaQLLzGKvmBpWnh/roU+Os9n58Xmc2pST0Y6SEtbdDWQ04Z
0ZILLDg5NhEa7qaZPT4NwGrYGkvkHwdVX5AeEWdRB7wS6BVjjiivkHJ2sBZU
nP840ayGGGmkp4RgXkIuiJl37M/D6EcLGL8L9FmEp5FMO4F2+pAJ79G/yNF/
hmlnGzAXP1gn6SDvKalFGd16gT4YSDwfTVqqkLeDHKtEkhuEJR9NtUBvB8ec
DZS32co7QB4LdInQkMhS3KTTX/f74qhP5gmuqxqNFBHjhaDiFKf+auRKv+/s
XfCLll6WwNEickxAOGqhtxXO9tLeFjjdgj58nHp6Azlczv0Ff6q0gJk2sCKl
7xtwxANLOs48Nt79xHQfmheCZSlcUVBY9Va0zE7ifSXCmdHbz/wP4E+YZSOj
gPMGAivg3BBz6n9aDeY0cElP3WMklWmLZVT1AYOMJtrAPRu5PIS8IjjRSTol
aMrIwaDNjlGzY8hrBbNYCkc5U1bgtZAYQ+8w0znvNkO3CTlNyGGEDhMWQb5r
2M/OpD+u3YJdKDVmpkZMPJslcMQaaTWFW4yhQ9ogg9rXoKJ1Clot56lwSTlq
Ca2W0moJRy3la5Q+Rq2fSR9kNoSY9AFGnR+2oAZdiF4bptNGaNXhjAuVByqk
/nIsfBKucpCvFNFKIdY+0NUA79bym+/y23upvkFuc5XfuQ/5GzaH+4St91sf
FrwmJGBNZMDa8KA1kf7hOAyG8AOCuH4BHAwdxxc9KIrnh+MhxzcAe9SEWBsG
MCUeM+hIS7anJ05kJo7nprrzM6aKc2bLC1aw+awt+89vDDZUM/sUOBVWlfxc
VXSvsmChIt9bno+l0IsxLM93CfLs5bmzWbHpN34ISYxdlR6PslPJnHQyJZaV
FkcW5VLlZdzcLE59NU+v9R8d88PoYeKczPoMfgY5XSHuyUjPVOTkZNiUO3jS
E+Ryhzhd4RMTYcNmX40C9XaA2jKyMIuVk0S2VqEZN29+xmfSCSYdcNqBAwLh
sAKTklJ0k7IuUtgKO2vIllKipohdmsUuSyJK7rBLrrGLLhKGbu5/7/v8ZwX9
Mk+vuAG2naNdwNpC2nqoKQPTgL04AW1CwtqJXDLolsGheqoznl1wkl17nnIP
+CzqSa8YeAfhvIL29pOTPWhlCPwyRjt74Ggj03U204dmGF8HfzKR00JKlcEe
LiRrvuLs9SdvvE0tdjLv5J/0tLUM2Cqgowkuiqg5ETIXgw+OwCdXs2U5fu42
9lgFsAmQMQcZckhtDm3IAaLrhOQWrc9C5iy29CqyJLIbPkUPBa668DzHU8F3
VwHpNaCIB/es6342BC0L0a840A2gkTxirITtrCcn24GnFSz2Q1st/68b4cWX
qF+kvMlWcqqBWOwDP2qY01KzzHlD3wWVr6cbzvQyG/0rCnJFwWzcMwqooeaF
cKqf8djTcrRkRPP6B3NphphxGdMaZoTUnBosaR4snDLrNhROx0sGuGJG9x5s
KTJdNxp6og3YmoFLQk+Z4NQD7mZtzGidORs9Y0XTOEsOMwP5p6xw0sJIpGcI
uozQydDHc1p5djN3wkRNmNC4mR414eKPmgNs5tBhU7jJEDyk9TVpOCZMn5zS
yWmNjKsQ0/JBqBRRygEkG4BSIa2Q+mhUARhSvcpHK+cbNb7YfOoYEQzB9Gk1
uEJVCn+V3Fct91FKaMUgUgmhrAcJW6muRrr1rl9Hu89AP3egxzf+Jv9/jgRG
YNWL3hARvS4yKjJk3Wr/yPDAyLCg1REB4eF+IaE+AcE8v0AO15+mfSmOHwaQ
4xPA8wvCv+8TEJIYN5aS4EiJd6RhEUxxpieOZybYcpIdeRme4pwZnPuw5GHt
+43B/18KS3/FDFYVLpbnecvznBX5HobBPFdZzlhZtq0i25GbkH/nSlhqwqrM
JConHeVlgcxEMiOBXVpM1db5FRfwa8q5Oo3v6HjAuMPXzexTYAxDseq5XCEe
d6h3MszrCZn0BE7i33eHOJxhE+MRwyY/tYzubAIV+WR+Ois/kTBIuUvzPjNe
ntdBzeCyM5c+2C1IJyHlPYS8Cw62wO5qor2CqC8iyjPY5QlEyS2i6BpL8ANp
E/n+90feryvc+7PMAt3cEDneCyxNYKQNepXU0hgmEU1ISXMbcgxCl4Qy1qPu
OCL/PVb5GTTR5ruio2fwu1GEvSjH2wNm+5hds3smZK0GtlrgaoGeduziEHP2
QYG0eaQ8nui7Th8KW3X1LbjUDzEOP+ppdytlyGHbqrAUggUhtJZRzecDnl0L
uhIiXS3EeBmwlJKd34DOC6DuHBgqomVJ5OANvrnQZyiPbPuGkF9jtX1F/X41
eeFv/KW+AFcTMuXQ3dfheAt/YTBwsp5Ywhy18yyZ5FgR4awj3c3AUQN+lqPW
q7yjG6Ei2x/7VVc1mLkL7suZFp17Op4633e0OXBBETHdi5bEjAL+aODd1wNm
4VTOne5h+txcAwC7cayV81qKGbGoB3N6alqBXTpGGC1iBlVwSc0celpi9i+Y
vfslE9MLhDPm1CA1XEcOtwCvkp42Qozbg7sz0OwwmhkGzCUaVjg3wswx9poB
DumTJgwgcpsot4XrNHMd2IWakd2E7ENo3EhPDPHGTL42U/DIUIhV72fWcE1q
ZFZRRjmtl1IaKaUcRIoBqOhHsl4k7oXiXmpwgBaLeDIJXy3nqhVcLJFYEHWM
U/XVafz1Gn+dJlCHLauSp1FwNTKOWow0IqTupwc7ON3NnI5mn452ft+Aj1jE
r6/jfXg8dGfMltVbtq/btnv9lu1rN2+J3LQ5LGpd8JrwgIhQDGBgWLh/SKhv
YLCvbxCX509z/Jji+XH9ApkpT4GhfkGhCbGjWART4x3pSW6cBDOTJjISbNnJ
Y3lpjqJsryB/obLoXm3prxg9LIIMg1X/rSn/T3UZlsKfKosWKzCDuY6KfHdl
wRTDYPZoWZZNkG6uyBwqSihLvvFIShw7Jx3mZqD8LJibTmYmEYIiVF/nW1HG
q6mgxEJfpp3bHuB0h7o94W5PmJuZiBjsdAW6XcGTzBJNKDMDDQulM8g+FjRi
CsIuorUOCPJYBUlEfR7ptHFnZzgzHp9pO5qxoyk7ctvg+BAySEllD5C3kaIm
2FdLdteAuwKyOp0oS2KX3mYVfU8IfmAbOzi/ztO/Lj5YHveQi8PIISQtTaT1
LvRImJlmK2PQq6aGO8FYL3QKaUsj7Iljl5xiFx5nq3KpFQ1vVgKmhHBOTM/0
wdlB8r6BnhVzDIVsiwCM1jAbDXMiOCshdCWo7TJbFo++eC6s5Js1C/ht3E65
O8jZbo4xl61NJ7EaTndCYy4hjafKP+GrCteMVABLAdl/g930BXK0Rbg6orq+
Bw2fsAZvkuNVyFiMOi6Q4itAnQpe3Qq/fzXY1chpOw8MqUh0g595ihf/T19H
o8+PQuCpp4zxpKOSmu6gJu8SdgFY6YfFJ+n4N/krYr6rk/+TNnhlkL6vRT8Z
qKkB7ldPo4yP/G1VTMv3PSmlL6KXZEH3tLyZXtJ1l5zupzwiHIfBggotaOG0
Gkc/NKMjpmTMatWcHC6psAmHS0qwgEnUghU9WDE8OKilAzNiZG+BpgpirAN6
tWjaAGZMcNaMZsxw1opmmVFXYHYYzjDThplt/ckhNGmmJi0ct4VyWZDLgjMg
nMA1BCeMuDjj5oAxc4jN6D+s41i1tFkJzThly5BRQukGaY2QUvZBeS+UdyFx
JxB2AWE3EvVSwj6MIUcqolVijkrO16r9NUpfjcoHA8igp+LrVDydgqeV0hqG
PqjsR5JuONDG6Wnn93YGDPQH9A34VpYGffVJ9DP/u3/X/idjHvr9jgNHYnY/
tmnnnqiYbWu3bI7cuDFszdrQiMjgsDD/kBC/wGC/gBA/rHr8AB4vgIefWAR9
g3398beYKU+YwdQEZ2oCDoOezGTMoD0jcTQr0ZaXai/K8gjy5ioLVmoe2NH/
j8Ha8v/Ulv3yIBUu/8Ygpq8ifwp/IcgaEWQOl6Zpy9LUNenG0rTB5NuvpCaA
vCyYnYbys6mCLJiRyCopAI21VG0lv6yU6uzkm82BzFBBOxa+CPdkhMuNY2Co
wxnkYAajMQs13knMI9/t9nWMB4+YA7G1aK4lyrLZBfGsFgGcHPed9/JmPDQG
0DsBmdv6hvErRRmlUN0LFR1Q0gQG6mBfPWouY1dnEVVJQHCTVfgdWfwVqW1E
P0/DX+bgz3PkfTdcGuF4ZMDSyLLWg0kxvWQm74+Ts0Zo7YDDrcDZiyw1qD+B
VX6anfUGW5LGWVbRi1IwLYJzEjQrhAsS8KMBOtspdSYxlE9YS+BYDXPcT1dI
1J9nd10DmqzQobKIiQ56rApYcoiJRo63L0QWRygxJtXQXsnWJZPmLHqogFBn
sPTZQBJLVH0Mxen+9p7AwhOw9ATo+o5s+hyUfczvv4mwNVUlkYUn6NbL4a5K
WnSV6viOkFzl/H0z9WwU2Z3A+a+ZdlUB/U2WLQ/MtCIc+lxlcLqG1MZxXY28
8Tqq83va2+l/T+FzX0/8YoCqQu5z69k33+b8quD/V49643w++RPoTAgaK6bG
a8jpHuQdQJ5+uKCEC9h2qsGMFi2pOG4FZ1bImZUxp4ZX5HBZjnUQA4hWdBRT
zMkRMNUHbZXIWAIneuG0htlpnR2iZoxwzozmLNSsCTBd7hY0PYTpw9pHYfnz
YgDxv99EOXASNDPXdkwYwChODQZ6bIg3OuRjM/iO6PkjOmhVQbMCGWXQIAVG
KWUQIU0fVHbil56SdUBxBxzoAP0dsL8dP0E/dkd9HJmIq5L6KGS+SgX/AYBY
Cn10GEAl42A1EqQdpLV9tLgb/xSvF1enn1AYIJT4tLasvn7p4LN/+cuhR/6x
/3d/P3D4uQOPPb3/kad2P/z49n0Htuzcs3FbzLrozavXRUVGrgsPCw8ODQkK
CgkICPH3C/LzCfLjB/n6BPn6hvj4hfr5hwYEhPkHhyfEjqQm2NOSHOnJnswk
d0biRHrCSGbCcG7KWFGmuyx3tiJ/ofo3BqsYKWyo/K117dcHDC79hh5msDxv
sizXUZphFaRbSlLVgjRFYVJv2p22hKtVsT88n54K8nLI7FRUmEcXF6DcNFZ5
AWyopWtrfcoFVNtdjskQNGELdtr93e5gjyfC5Yl0eyIcrhBmQqk70OMNnprC
GAa43T4OO294yFeBg3A1EGSy82PZPVXMxX8L0/z5Se60A06NM1dkuofJcQMy
SaC+B6raSFkTFNWRA/WgXQDrs4maZFJwnVX4Nbv4S7apg/OTi/uTl/jRC+7Z
wfIInFXSI03QUgvdA9SCntl6WDChsS7S2kQ4uoCpCogSYeVZduY/WF1XqEUJ
vaQkZwbJBSk2n2BJwZz7w/ZSkUgY89hD+aS1FGAkWy6AzivIks0eE1DGUqTP
xd/Cf1ToPWW0MpUWXkeTHdS8CI1Xc2S3SNlNQhxLSpNIYwbZc53+6Pfgyt94
KS8Qef8kSt5clf0Kq/pDCgfDgcvsgQuk4iapSyFs2UifBhUJUHqVevcg+cVf
+B3f+noaKVs5qb1FmlNZpgzSXkGNF0NHySq3APzUA4tPoOOPou74wPsS+kcV
/FFBln9G/S0amat8ftVT95TU6Sfpx8LZae/hnyLdLWBaCJzd7DkpWlCBaTlz
EnlWSakKQsc6o2dxKMDoSeCyFC4rwTKTBMGyhrqn85uTI28vsFUjYxHp7AVe
FT2lQrN6akYPmfHCRmao1LyZnh1CM0bMIOX9Tf7MlIe5vxu5hxBDnx7iGsf0
GbnjQ/wxo8+wFg1rwLASmXFal4AhCTTJKKME6fpJTQ+p6oTyNihtg+I2IMIM
dgIGwDZyoBMKe2hxP1ch8VHKfFRKH7WSr1FwdApap+DqGQeLhsTUkIhW9tGi
bqq/kzvQ5Sfq5wn7fFvuRudlHPny3GsvvfjZ7//3g8f//MbvHv/HI48/e/Dx
owcee3bfoT/uPHBo+76HNu/YFbV567qo6LVrNqwOXx0eGhYWGBocEBrgFxzg
GxzggyskwC8kwD88yD8sKCAsMAgzaE1NnEhLsqcnuzKTPVkYxt8YTLYVZzjL
cnDcm6kqWqkp/c9vdvT/MfhLDbMys/KAQXtZrr08z1OWYy9Nt5SmDhUlYwAH
s2615MW2Fdxpy7peGXf5lbREfn4OmZVCFuTQpYVUQTZRWYpaG7ktDXR1Bd3S
yFNKAkfM/o7xQJcj1DO51j0Z6fKEOFwBdqeP3eHjmvT3Tvl7vf6T7gDXOG/M
TGlldFsNKE0jCmPZwkbuvIe3MM1MoZ/FwXAMTo8BzzCw6yiLCA51Q3ULkNUD
cQ0hbgSd5URTNlGfSpbfJPLOs0vOk9pqzpKF86Md4VoZJZfNTH/y6F0S42bv
gAta4qcResVCOYWE9S4YbaaGawlxCqg4Q+S8SraeB1PdnBUVNSclF+XMwfZ7
SmZHAOugPIHUZ7G1qWCshjM7SE92QEUKUCSxe+NA5y3gvMsp/oKT/F5Iw3dc
TTYaq4ayJEqTw1FnkO3nCUUypU5HstvYjnI+OoiS/unfc5Hbf5XsvECW/Zso
eIVd+wHouQy6vyN6vib6L5C6JKCOJ/W3CG0CuH0U3L3kM9PCHS8ibPlI8j2h
vM6yFdALXdR4PjGRx3YUsWebwJVnwe8jWSVnfX6VwYUeanmASnmDjnud81+N
z69GYKvjPr+NeGkPkN7iOmqJqW5kbweTfdx5OZyWkF4pmleh/gyfE0/6KtPD
l2TUophcklDLWAfVcEXHdN8tq9DMAO3phCMVSJVFjndSXjk9jT+vNMxk1HkD
Na9nhlY92FjEmkhNDzFXaXhN0GsCk9iLPkiCLj1+EaFdT00w9PFGDZxhDRpW
oGEZsoihRUyapMAiRWYRNA5AQx/UdgNVF5B3AFkXlHaRkk442A4H2knGi3ZB
bEcH+2iJkKuQ8rAR1ciZxKfHzlNGqwehXsL4WO0ALe+lxL0cUa+PsM+/v3d1
Z/ueuvLn8tL/mXD9o2+/PP3ue6eef+GDP/zPO4f/8MqhIy88cuSFg4eff+jR
p3Y/8tjOA49s27Vv87aYqOgtURuio1avWxuOLWlEWFB4sH9IsH9okF9IkF8o
Ri8oICIkMDw0MDwoKCIx1sLoYKI7I9mdnTKJvWhagiUz0ZqdaM1PHy3N9pTl
zlQWLNUU/1xXwTD4wIv+WlP2c03ZT1XFy+X5k2U5tvIcG8awLGesOM1QmKws
SBTlxXXn3enIv92cd70u67Ig8WLZ9z+cvhUXlJtBpCWS6SlEcT5VnAfLikFz
A6/1Lre2hq6r5nS18XRKv/GRIIfd3+kMdbvDPMzSKNNB6nDwnQ6+2+k75fHz
un08E1z7MGdISXfVE+WZRFEsW9xEL3h5i9P0goeed6HpCYI5+jdMOXVoRIzM
PVDbAhVNpKyOUDRRfZVEcw67NRs0JRKCb9n5Z1c1X4X2bmZu0pKRs2QEiwZy
RskMkRipY483smdE6N4Q+nGEwqnH1gjH2jlL+sjRu34NX68qOsaqfp80FtOL
KmpJRWEVWFKiJTE91QsH49jCG2xZLLaglD6fYyhFujzU/DWr7QopTec4GtE3
L4F9gUTFBf5YCVuTCio/Jgx5tC4TdV0kNGnIkEUN3mJ3X4J3P0MdF6HoJqlK
JE1pUHOHW32CjUkcvIWkcUTrp7D1M0JynRReJAa+JWVXSNUtLLicMQGU3qSH
cgCGtOtzZsnUVkLYiojxIuCtRePl6MND6PXdwFrps9AGXTXETC2pugPGq7n3
JNR/5LTgU+7/riHzz9GOMuBuQo67pKsdzAm5nn7aNYCmByhrA+fNI+jJKNR0
JfAXBVzEACqoFQyghlHAOTGa6gLOFnKoBCgyWWOtzD7glJKeVjHTM5hZOgbs
MZgBNUyiNEBsTaeMcNIIvUM4CUKPAbr0yKGHDgOyD9E4/Y3pKJuaGlGiEQWy
ygBm0CqnzDJgGgRDA3CoFxh7gK6LxAAqu6CiG8p6wGAHIcYMdgBhJxT1IGEv
EvVTEhFXLuYoxJQax0YZRydBegmlF1P6QUonhMo+StbPFff7iHojBrq393Ud
7O052tX1ckfr8021R0vznku58fxXn7zyxhuvP/3M20f++OqhJzGDRx858uyB
R5/a/8iRPQ8f2rH3wOYdO7Zs3b4petOm9Rs2RqxbGxaxJjQ8MjAsIiA8IiAs
PCAs9AF9YcGR4bhCIhNjjamJ4w900JGJpTBpPC3RkhFvzk6w5qYOF2c6BDme
8rzpqqJ7WP7qq5mqLfsvFsEawY/VRdiLMgwKsm1lOeOC7NHCVG1+ojQ3tjf7
VkvW9YbMa1WpFwuSzifHns/99mLtl1c/uhUfmJMJ0uLIVGarApbm0qXZsKEK
tNzl1NfQNRV0cz1XNsgftvg5x7E1DZj0BHm9AZOT2KP6OR2+jgm+y8GbdPtM
u30mHXzHCIWDQH8TrMpeVXSHPVAPF5w+92Z8FybJRTeaGwezo8wqt1uPxmSk
uRdpmoG6ASjqSE0LEFaRLXmsnjyiKw3WXmEXnSEEnxCmSmpeSS8yLcqcaQUx
IyO9A3C8EY5UE54utKyBP1lwFALiPK61MXy0iadKA13fs8reY5f+m9V7Hbk7
+ItKNCcLuGeMnB/0VabBxs9XtX9DtH/LqjjFarnAsTcBaTLVfQO03UQVp6mL
z/Afj2TXX/RRpFO9V0HTZ6SlmOy7SRa8sarpLBi4gsSxqOkzouwdIvcVovYc
u+IdUvQZazSdX3+G0/4lmm4BlgK67zLsOE/KbkNlPFIlQPkttuwyaUhkm7OA
Pp0WXUdNZ1gN77OFF4Eqjq1JIIzJxFgh25rHO3mQSHqd52minJXAXU44c8FU
IXQLSG8NmG3mnHsUfP0MD3tXewXpboT2RhJ/qri6CHsbHG0nx1qo717jP7GF
/vdjXFcH956UOfGxoiTva8CSDHm7SHcbcLdBUxkQpxLDjZRbBKfk9BQzHJWZ
jcMcQtT9BiCzpThjQNN65obEySHk1gGXFjo0lF2LHAbaYeRMaNGYCoypaJuC
ekAfsKmoEQVlESOTEFj64VA/ThykvpvUdpPqHqjsBvIuIOkC0h4k6UbSHkrU
jQa6obgfyUW4KMUg0oj/L3eGQWw+acMApeqBil6OrC9Q3Bc+2LtmsD9KKt4p
k+6SSHdLpNskwi2dLTtrBHvz4h+58uUfjh97/uhzrx3548uPMDp49ODjz2Id
3H/o8b0PH9q57+Ftu3Zti4nZtmXztuiNm9dsiApfvT40Ym1QxJrAiDVBkWuC
I1cHRUaEREaErWYqNDIxzoS9aHqSOz2F2ZvISBpNTxjKiDVmxQ/lJA8Vpo+U
ZjnKciYrChZqBL/+1rGGRbC65F5t8UpV4WJF3qQge0SQZcUACrJGClPUefHi
7Fud6Vdrky+XJ35XEPtl4o1zV66evfT1V1kffV/4+bV3frgVkZPBzkoAqXfY
+RlkcQ5RmE5UMb6U31RHV5VRdeV0dyvXoA50TAQ6mSNgPlNef1weF/7az+PE
GNIeJ9Ow7XHQjmFgVtADTVRVBlF0k9VTypkd970/Ry960LKbXrCDuVEwO4wm
jcS4DFr7KEMzoWsktQ3Q0IbENaA9i+jPZ4vyYXcau+4SW/Ah0XUN2hrQzCCY
FVPTA5ypAeacnbsNjdURrmZyWcYc5cv/DJ14lNN4lYPVRJNJdF8F1R+yS/7F
qjpJCLOo/nSeThAqy/WzVpAdF4iaD8n2r0HVh0AYj6w1oP5bSnCaXXiCFHyI
hQ8k/ovff4db+SkU3kKqeKDL51lrojou+TZ+yBZ9D7UZsPt7ds0pWP8RLbzN
j/0zmfYceet/4GcPE02fku4ijjWDW3McdH8LzcXAXg+cjUifiQa+YyvvIGsB
cNdSmiRU/m9W3furJNdh73lCfIXQxAJTCns4i6g+x7EU+A5nk+YM4CmF7krS
Uc6eyCKm69FYKbjxoo80y9cjAI56OFZDTLYiTwccbSDG6khXM8z6mPfx00Gv
7fPpTPDFWfLBLgZ24PRUJ3I2AVcr8HSybfWkNJU0VZPOfmpSxJmSErMKiB3s
ogYtaNDsg1n9szo4rQfTeswgc72US0M4NcChZUQQGxi7Fo4rAX7hRmVwRAJH
pXBMTtkkcAS70AFg7kPmXojlzzDAGFFjP9L1QVUvFkFS0QNkPWiwC4q7yMEe
IO5D0gFKNgCVgxDTpxEhrQgaRNCEGRRR6j6o7OHIe32k/Xyp0F8pDdGpI3Ta
1VptuFYToVGt1mkiNfJ1Ax3RDVU7i1MP3Pj60Q+O/fno8y88/ocXHzn83MOH
/+ehx/60/9E/7Hvk8N6Hf7d734Edu3dtj4nZvm3z9uiores2bIpYGxW2ekPo
6g0ha9aHrF4XvHpdyNp1YVgf168NW7c6ZG0ikwcd6Ume9GR3Roo9I8mWFqdP
va3JiNNmJ+oKUs0lmVjgXOX5M9WlP9aV/wdjWCO4X1W8UFW0XFWwUJHnwQyW
ZlpLM4fLMkcKkpQ5sQMZN1qSLpXdOZ998/PEa2cuX/rg8wsnvvz6TOaxzzNO
3rp66oc3v7kcnZHGzkpGSXeIzESyMAtiDAVZRGMFp7GGri4D5fmwthTJRLzR
Yax9XJed7/X4Tnl9sQJ6H9SkkwHQ40CT42EO8xqLCgw0gOoMVvENdmsWOTXC
+3GOs+QByy5qcQItjMF5G+k1Irsc2vqAuYU0NuEiLJ1A0QC7skhhLqkogYoi
ciCFaPiaqP+cFN4GpmLkbAaudtLVASe7IH4HYj/mbiN+VnMTT/pu4xIZH/En
cWYsJjTZZP9tdvNnROW7ZP4/yMS/0a8doN45xBmtprQZaPAOqUrlVZwArV9D
QzFMeZN9+yi7+wdkLIb9V1D9Z7D6Y7LhDNRnAEUstzuRNyld7+2NMGfCsUzs
A/n6HLr+Q3oomx4p8Uv+G+dkDOuZIPY/1rEy/gpl38KBb1Dei2TOc6DzPGIO
8xaivqtopII7lIskN0h1AlLcgv2XaX0O15gBW04RAxcJfQo2tKQ5nj2eA6Zq
SXcZ6awCE4UYWDR7F45lg/FSaC8gx/L5c+1wph1N9/OW5QHT3aStEpixmy0n
LFUh1pZ9qacji8/7/KzirEjAgpia6aTsdWCilnS1AGcHHKlF0jRCV0y6upmp
wlNiNCdH2CQsYY+hIGeZm2iYizBmNcwdUlNaNKkFTOmgRw+dOuDUIIzemBSO
S2jbILRJ0KiUYm79FpHDA8A6AK0DyNQLcQ0JoVFEGYXI0I+0A1AzANVY7zCD
vRDroKwPyQYohRAphAyAqsH/S9/QIDIO4p8C6r5Vsp4AcW+kUhys04QOGUJN
xhCjIcSgD31QQXpdhF4bqZavFXZtaKzemp+648r5/e+9+eTTzzz96BNPH3z0
z/sPHdnzyKN7Dx3a/fDBXQ8d2L1v367dO2Jitm7bsnH7xg3b10dtiVzPDGYL
X7cRV9i6qNB1G8LWbwiPigrfuCE0al3IhgcMjmMjynSKJo5mJI6mxhqSb8rT
7siz4pR5yaaiDJsga7wiz1tdvFxb/nNd+S+1xfeqi5Yrihar8mcr8txY/koz
zGWZFkGmtSBJnn27O/VK/Z2v8699Enf5o8sXjp89f+zdL9766Ny57FfPJh/9
9MtPU+P+efnMe188mppA5GSh1CQy5TaRlwJLMsmiNJYgm6wVoPpKsjyfKE4j
m6s4ahnfZuU4xrluB3fKzZ+aDPJiZXTzpz28KRflGuO4bTyXjRxR05Jm0JRN
CG6z6pOIMQX10zR/ZRItOsGyHS2OUYs2as4MJ5XQIaJG2qGlBVrbgK0bGttg
F9ayVFJRCIbKwVAFVGZhQwibzsPm84Q0nrCWgIk66MAf720kJnFuALTFUnv9
yYS3eT/K6PEalrmUpcsglUnkwDV27WlW9qvgXwe5f1zLEWdDs4CtTif6b6Kc
10DredpWiSTpfk0XguVp/rpcoM+BNedYic+xu77lGnJQ5fvk9RfA1df4Occ5
DadA/Xvg9lHq7AF4/Y+g/zNkz/PJO8WN+1tIy/dbrj7jezKGffk5eG4vKD/J
7b9KC6+S8kTSmMXJ+wco/SxgspNjr6FshVxVHCVMDFzQ7DBkUJ2nSW+z/68a
eqwYaK4S5hzkvhtgLwOuEnqsADqr0cqgnyWbbcshPWXEbAM520QokkhJOn+m
P2BFQo2Xs22FqO0S39pyWFW5re68349SzpKQ47kLbKXkeBV48F8EHW1wuI6U
pROqTOBohZN9YHoQzsvQooJakIE5XArmJpp5NTWvpWbUcEqFvBrmQuFJA/Lo
KacKuhTQIUMTYjA+CCbEaEyM0QMjA8AmhCNCMCyE1kE0LMEFrUwhkwgyDAop
HQMgUPYBeR9Q9EPVAFAN4CdkhA/TNwgwfZZBHCFp/QBH00cqe3362/d39z6j
1m6xmEKGDEEGbYBWHahRBauVwUplsEIeKpWsFg+u7u/e0NawubJwU9rtLV+f
3vnaiweeOHL4wCOPP3TwMOYu5qE9Ox/atePAzpj9O3bu3b5z15bt2zdu37Ih
JjoqZv2m7ZEbfsNwSwRzM3B0+Ibo8Cj83BQetSlsQ1To+qRYS0qCLS0Z29Hx
9ARbesJIyh1d4g1pyi1p1h15bqKxKH24NNNWluusLJyrKfuprvznmuJlxoUW
zjONarlOxohmDJVlmgSZpoJEadbNjqTvq29+kX3po6tfH//882PHz776+tm3
Pv7gk/SXziX84cSZl7+69EnmhZc+f/u9L/Yl32HnZYCcdDLpFistjl2UgUoz
ycIUVkUu0SCgKvLJ3CSWIIPobaFNWv6Eje+aoL1OzvQkb8rNwQBOe+gpF8cz
BjGDTivO7FDRRrbmEWU32dU3gLWH/mkG3vMSSw64MkGvjMKlYeaqL68aukTU
aDu0tTFnjhx9nOE+ojcPdNwhZbmkvoywVBDGfKxuRNctUHWGbDhLKJLRSCU5
wdgwyt0FJpo4r+wB7z2OpntpWzE0FZPaDEKdQiqT2QM3Yf0ZdtIb1NkjPgNJ
oYp0QhRL9N4hct8GZe9DTQGhLt1w37hlMMln8CYaLkRdP/CyXierPqBavoWV
7xPXnyK/fAwJ3uckP09+8jD76CbWC2tZJ7YT+W+SGW+Q/9gOa04Fz9VHDRVs
+Oww+vsasvrrwB/1fF05t/WH9fL0NfIEJE70bTgfoM7iTbZR1kLYdInzw99p
aV7w4A/ctg9ZqkQ4KkCOcl9DEuiP40z3rrfm8uXfEarvSdk1tuQ2Z7SAmigi
ZxvgzF3OVAUoeY+4+jqn8SJ3thN5aoiJQsIs2OiR7pxo8ZnvBdMttCUXWHLY
9krouguczdgqwNF6QpsDlGkUdq2T3WBGiOYlYFEO5yRwRgxnpHBGjuZU1KyK
6Syd0gKvlrlR0auHHg10K6BLBp0SaBdDhxTh54QQjAvRmBCOitEIJnEQm1Jm
UXREjkak0MosjUKzGA2JoK4fYB1UC3EB5jkANEKoFSEdLiHSY04HoUmEsPbp
e6GqnzXYs7e+/Z1u0YtW89rhoUCDNlCr8lMr/JUyf5nUTywOGugP6ukO72xb
13J3TX11lCBvW0bc1itfR596K+aZp/YcPLh3z769O/fs2r5na8yeLTv3b92x
f8uufVt27d68a+fm7THRO7dE74reFLMhOmbNhm2RTG1fvWF7ZNTWiI1bwqO3
RGzcFhG9NSI6OiIq+bYxLd6akWjDlZYwnBpnTbmtTbwhSb4xmHFbnJOgL8qw
YKtZluOoKJiuLV2qK12uLpp70KE9U5bvKc+dYBQwwyhIH8Ik5idIMq63JV6q
vP5ZxjcfXPzs3x+f/sebp156+cNjn/zrTNxfTl//48kzj5848d4PFz5L/erp
08dPfP5QYiyRl80qyIFp8SDxBis3hS3IBSUZTKN1VSG7spAsSmUVJLIby5C0
j2s1cJyj9KSTmnZzZya50y6aIdGFvHbKNQIdJnJUhfQdqC2LXX6NVXGFNLTS
v3q5P3nBiou9MkEujwKM4aKJmczgFsHxTjDaSk50ANcA5RikpMVk+y2WOAPo
C4GxgDTmEvoCUppJVJ4l8/7JvvsVqc2CE42Eo4H0NFG5J+kzfwoxlPobM9m2
Cqxo7MHbhPAGgZ1nx2Wi6hTZ9i3df4fX8QO78Ty4e4lqvoi6rqLmK0TicZ6k
KFAYB3u+IwtPwo8Pgm9/D3LfJO9+CpXJoOAYkfcaZS+ljbkBXz/O/0sY+9gG
9msRxFu7wBMbwD4+6+yhVZ1nYPo/0fF9xHtbyc7zfF06NNWsnxh4qv1qaPlb
ZN9VwpoDsfzJYjniO+DaUfDKFpB7HKoz4OB139aPQMNxUn4LjpXxMt6mck77
FB+ndcmENZNQXUPC79iWNGIki+WtpWaaeY5ClP4meHY9Jp273I9cxcBdzPK2
+k/Lty1pIlb6aXcDsBWSnmqEPbmzAdgbgLMF2eqgIpllFSBXKznTDxalcFEK
5kRgRsTMNZ1jdhWxDpLTKnJGD2bNcHaIuQdnSg28KuhRMt25bhlySSmnhLmy
yi5iLvsexyVl3OmEEo3hQIFNqYwhcViOrFJkFgOzGBrFlB7rnRBpGO0jtYNQ
J6YYAHFUFCHzIDU0QOp7WJouzmD3+pb2d2s6rvRJnhm1BA8bgvWaII3cXyHx
kYr8Rf3+vd1+HW3BzU0R9TVrqso2luRHZadE37my5bvPtn30ztaXj+4+fGj/
nj27duzctC0matv2dTt2bNi1O3rP3k179mzas2vznp2bY3Zu2rN1y97obTs3
btqxbmPMmqgHtWHH6o3bIzZti4zeunrT9rVbYtZu3bpmc+JtbXLsSGriCHah
6XHDqbHG5FvK+GuixOsDaTcHs2NVhTgSZgwLsscq8t01xXO1JSs1xYsVBZPl
+ZOCfHdZ7oQgyyzIMAjSDPiZnzCYfu1u/MXSK58kfXXi/Ok333//pVfee+Fv
77157u8fXP3zqe9+f+Ls48dPPXnyg9Px33+c8N2fT515+9PDiXF0UT4oKUGF
OSgjnsxKYJdmE5VYzjLJ0gzmQG55DsGcxs0kWiqxzUCjRto1itHjz3p8ZjzU
jAvNOGjvBHLZoHMI2ZWUvh11FZBVN0Hl92xVNTVr4vwyCe47yJVxZkD0spm5
k2hWDSYHkaMHTXSQjk7oEVIuMUdVBrtiWYPJQJ0DNLnQkEfo84A0g2j4ip3/
Biz8N7v+CyC6AY3ZpC4D9d32NxfxDNlsqwBaBKQikWy/uOruZ4Q0FY1W0/JE
WHaayH2HVX0WyNPgUCElTSOz3gFnn6AuP0cXH4c3nyJf20o8GQz+tZ2V/iKs
fQ82f8eJ/xf49nek7Ao91RBR90Vg1r/DtHl7y76IemkjenGr/0eP8J/ZQL5/
CP7vOvKVrfQbMcT1Z9hVbxPtP9Aaweas1wOSnmFl/4OoOAZFX6P2L0HNCTLz
RRD7PFV/Ao3mw6mqIGeJf9c5tvAynG3hJb2Cnt1Exr2BXLXInAUkF9iqq2xL
EmlNJR0l0FVNuivgxaeot3Yhaylnrg15SkmPADqKQfv3hL0taGYw1NsM3fUA
A+hoJHFYnqjHnwbUnCR4vA7ZG+BUD1iQUPNiMDNAzomoeSmclzNDTWdVYE6P
5ofQghU7kwf3kA7BeR2WRUwinFKiSTnllkKXFDmkjBqOY18qRw4VtKvghBqO
qx+MPX8ghcNKZJFDiwyapdSQmDIMUrpBpBc/qEFoEELDIDAOImbRpoel66RF
XZsaOl6s7vy6RfiOWrVtdChoSBugk/orRAHiPp/+Lp/uVr+WRv/66uAqQXhp
4dqctPXJsdG3r2y8+OWWM+9vefv1mBf+svvIob37du3ZHbN9x/YNMdvXx2xb
tztm/d5d0fv3btm/Z8u+3dv279y6a8eWvdu37d8Ssyd6264Nm3eti969dtOu
tdE710bviMDulAFwx/qtuzds37l+W/Itc3KcOjV+JD1hLC3WnHrblHhTGXe9
N/56X8oNUdZtWX6ypjDdKMgaLs+xVxUtVBfPVhVjAMfL8ibK8pyC3LHSrCFB
ukaQqilN0+TF9+MwGHuh8IdzsV+8+9mp1987/rc33n7l38fe+ub5k9///v0v
nzhx8sh7xw+/e/LZj85+X3Lng7hzR975+M3TT2Smo8pSsqIS1pZTBVnsrHgc
BkF1EXPJYHEKIcgg60pAdQEpyGCXZ7M7KoF6gGlYmpyAU04456EXPfSsE03Z
4dQo9JjQuIpt7kOSSqIxjlV0nlV3lbS0cu+Pc362g3tjYGUYLpmYwdELGsQc
A+yHzi7S1QOmhGhGTtna4EAiOXCHUKdDdTpbm0WoswhxCtFymS04wcp4hUz+
K1FzhpDHQekdIEsgRbeBLhsOlyF1HuiPZ3dfIx111GgFIbpFtV4gKs/BsjNU
w+eg/TzR/CWZ8za4+Cci7hnYf4tz4SnymahVT4WR/94DPz9CX30e/mkt6xB/
1Z8DWZf+AkpOgr9vJrLfAs6CtYrUiA8f86n/dv1oZVTJ2dCjW+iP/uDT8sOG
O/8KeGsnzHyHKvyEH/8awIA3fwtjX6BP7yHy3+L23UY1p6mKd6nyt9gVb7Ez
niZajwPZd7zuj4nWj9iGJFRzBvxrG2i7EuJtgIqrxOAXhOYqy3AbGBLYlgyI
U6GziEx5CVZ/xvWUw6laNH+Xs9xN1n+CPjiMxKl+9lrkqoJYCheE9GQre6qJ
LvyQ2/It190U5OmC3k60KMHyR3l7yJkBuCBD83Iwg0vFbEbgRLBgYY7Y49di
2UKuWNDyEM1gqML6iBMi7ZZDlxw6VZRDTTlUyKFGdhWwq6FdS01oqFEVxIZn
VI1GlP9vv14KTRJgkqEhXBI4JIYmMWXBDPaT+q5Vmg7U372xuu3lvLoTDd2v
atWPThhCLVp/lSRQ3BfQ3xHc1RzUUuffUBFcXRJRmh+Wl7E2I3FD/M2oK99u
OX92+8cnd7z95r6/H334f/+w/3cHHtq/a+/emO17d2zdsyN6d8zG3TFRe3du
2L9788N7tuJ6aPf2Azu37Y/Zvn97zIGtO/dvitmzceu+DVv2rdu6e+3mXWs3
7lizefsaBsA9Udv3RO3YExWTGKtOih1Ki/WkxtuS40aSb48k3NDfuSK684Mo
/spg2g1xTrwxL8lSlD5amuWtzF+oLpqpKvKW5znK8sbK8uyCnJHSTENJmro0
RV2cqsIMplypu/NN3vdn7nz+1mfvv/rv43//1zvHPn3t5I3//eCHJ06cffKd
44+/c/zwex8efvvUP7+7EFuZ+cbN04fffv/EF48VZ8K6arKhATbf5dZWkoUZ
rOJ0jCFZL3gwpimdVV8Cm8qpuiJQmU3U5RM9tZQBf1SOUJjEGSexOEktYF86
Drw24DVR+CWz9LHlVag5kRR8s6roE9ZAJprV8H6xUz+NE/hFXzJgDOGCGjB9
1wPA2wunusH0AJyV0a5+SpFL9t5kGUp9XX2BjiYfXQZrMI5uu8QSvMcufAsM
pnB0OVT7edBwjui4TDZ8iwRf+doaoLGcJ6vfW/51YN2lNcr8fYZ8ErvB1NfI
hBfZtScp5W2c/oik1+Ddz7kjuUiaxPn0cfDNHzny9DB5duTpw/TvwtjvHOBf
eDb4qdXE01vQDh/Wu/tZguPE8cPgiXAi9y3Y+z0t+BCd/BP36lFu8xd0/7ec
S0fBU5HwaBT98QHf9ks8ZQ559hD52jr20bXo9CNU/ls+A1e4hnwq6xj8ZA86
t4/1wxF21Xtk/5eE9BLRd4Fd/wl/pJjnLgfa26T0G0JzhWVOIR2VxHAeaUkh
GU1MQeN50JJAT+STTgH7fj8V+wbnr9GQGaIoBPZK9kIP9ZMCzXUQjV/Rr+xG
8Sd86i6iuT64KELzQnKyA9tRNCdBczJyVs6shc5oMIP4MxAtM7NJyR9tFK4V
M1gyMhfAYX2c0pCT2gfZUINcGoqRPzVp1wCHBjq00K6DE1pcaFwLxzRgDGui
ihqRQyYeqiisiVYpZcH0iShDL9R1sg2dUNqzua7taFbluyVNb4vFB22GEKvG
VyMKFPcEdbcEt9YFNVaEVpeEC/LCCjMjs5PXp8RuuP1D9A/fbvn6061n3t/9
3r8OvPbywef+8tjvDz/2u4cOHtj18EM79z20c+e+Hdv27dyyf0f0/pioh3ZF
Pbxny2O7t/1u97aHd2EGtx/cueNgzM6D23Y9vGnnvo3b9kVt2bt+2551W3av
37xz3dZta7fuiNq2J3rnvk27923cmRBrSIsTFmYLinI6ctM7sxIrclOuF+ac
Ki16v7LkVGPV8dbGUy31XzZVpdQLWqtLdDXFnqr8xbLsqdKs2ZKsuZL0yeJU
W2GSsTDBUJCoz74tSbzUdPOrgosf3/n02Bfvv/zm28+9dOyNT184fv0PJy89
+s6Zx459+LtjJx59+33M3R9PfnIuKS22LvH17z56/Nipj77aX1yIWpuornbY
0wXaW2FNCVmWza7KI+pKyKp8EmNYl0+2V8HWatBYStTkEndLCEkbsKoozwic
tsM5F1xwU3NYDUeA10w5NMDaBzTVRFcau/p7dtFZouI8kudh7eP+bGMGwt83
wiUtXJCDWTGYFqLpfjTTi6aFcF5Jz4g52iJSXcydV6wx1Qd33vTRZgHhLaIO
G8tkznQv31iCjIWw7wan9RJR9DHx1Z+ZJQ5DLifhTOTf9vKyv9y+pN49XOYj
u0DmvQY+O4SSnofmPMpaja69Tl97jpRchD1Xwet70M2XkT6WO1IScO4ZcPqI
vzQ1wtsanXkqYiu9agtv1cEg1vO7YYz/qt186l97ifg3wF9jiG0+q47uIDJe
J9P+Rb68GzzOX/WnQFbS28H6lBBTlu+nT8C/hqx6Ppx15gAU3+I5SsOavuJ+
upM8t4t8M3pV4t/9ZLd9x/KpkXwwcIHd8wkpukAYEymHgFZeJVSXATai9nLu
eAW0pBKGO4Q1nrClkaOF5IQAesuI4Sz07m6Q/Q4118qfbqIW2uD9QbQySIwU
oY8Ooz+vA6/vBqo87j0xvdALJ1vBTA/TP8OsxkigV4qmFWBOC+a1zMjElSF4
38LUigksm5gDhgtG5mpUpmtUDz066NJCpxo4NdCpRU4tdOiB0whx2fXkhA7Y
dciho8c1cFQNxrSMLDLWVEIZB5Cum9Bj+rqgrHttXesT+XWvlzW9LBw4PKJe
Y1MHqIXBoq7Qjuag5qrQ6uIIQU54QeqarLi1KTc2xF2JunEx+tJXm748G3P6
g90n3tn3xqsHXzx65H+eevLI479/9JEnDj10+ODuQw/veujAzt2YskM7tj2y
Y9PBHVGHdkU/umfb43tiHt217dCumEM7Yw7u2PHIjt2PxOw+sJlhcH/U1n1R
Mbs3bN25YfPO9Vux/9y9ace+rbv3b9qzP3pXQqwpM7a8smJzmWB9UfG6qqrg
lhb/7n5On8hfKAmSqQPVBr52yF9nitQaNyu1T8tVf5PKjolEx/v6T/X0fNbV
ebm1+UpT7dWGyhv15XGVhcn5qbFJV65d+eTyF2+f/vCVV9567pljL7/z6snL
z58698yHb7/w0T//+tGbz7z/zz+9++8jx04+/9G35xIuXCq58tL5s0eOHX//
q/2lJVRXBz3Yz5WKqMEB1NUCmipgbTHGkKgtBpU57NpcdqsAdNXBrgbYWgnv
FpNtpYS0mWnfdY+g6XE0b8cFZ21wyow8OibXm1qBHP+xiUTlN6zCD9nln5I9
sdBSzZ2TUz+Z6Pt6ZtbfAnOJGJoTQUcXtLX72lu50720tRr0J/id/Av13FZY
/SVn8CYpS4EdF2Hlh6DgHVKYgNqvw7wPQO677Jx3YNoroPkCvPEK+/hj6M4/
Atovo7i/cq4/yT65i3h2Dfjid3TTdwFfv8r7cyQ4GkF88Th95i9wG3/VocBV
F16g4t+CByNYr+2GglNQkehfeC7gy6Mht4+v/efv/Z+KCXgsEu0JWLVrNfvw
RvBQKPnqw36HQll/jYHPxhD/h6e3jq7iesN/yZnZe+ZYzok7kgSIu3uCFYoU
aSmlBYoXKIXiDnF3gwCBGJqEECVGXIm7Hbec5MSDfO9d694Z+rt3rWftNUkI
fzB8zvO8e2a/r6069qsja4shetgWyTsH86/SLvsxr29Su+hAPbQWeX2COhKv
8u66+l+G4JIl5boNkn4Q9EYxZTns3kR6zV28PxFvCwa9cdh4Jjr+HO+KQlvv
UloeUHpiKSNpgJdJFWTC8UdA+ArlPUfFj9GBGJB7kS7JxWQ5yGQeOleCTZcg
c+XYiwv4TgP04kZqTzbjWzOc/YjJy1AF2bwRn26Ck41k6T3dAQkGZ3vIBlBL
A+SBpi/D4CvZDRKQrwiOkX0wZkcIBsl2yvIhSL4w0wukfZh4ABcPAvEQkAxD
6Qi5kjAOkm+yiQYwQS/G7cDGifDZCAdqQF8lGKxjNFTqvnnnmJH707sPP7S1
WI53aY11qXY1qDd+0CnP036fpf7mke7zON2UUL04f/3wO6sDrxveu7z25gXT
y+esz520P/6n4+8H3Pb+5LPth00bfDZ6eWzycN/q7rLJ3dnP1d7T1dbZzcbW
zdrK3drC3Wadm7Whh816T1tzQh42Fu7Wlu6WVq6WNi4WNs5mNg7rre3+s0Ij
U2tDkkGrNSY2a8ysjc3t11s7rLUhrDApbiAlpj85Mjk82CgiYkVKPMx8rpyZ
sfJ9kU5dPauhWa25k02SOKDZN6Q1OKI3MqExylMd56tz+JocvsaEUHtcoDXO
0xrn6o9xVo1OGA+PmfT1W7W32zbUOtRUWleUWVVVONXXuTQ32bd9sujoXN3V
ubqhyaSs0vLFO9vH2Xvin/38KG9/2vsTZyP/OPD3gagYo+JC2FRD72mn9nXS
+rqoXW2goQqpyAdFLyhFL5DCTOTdE0pxJlpbABpLkaYy8DEfLcmiVL2CXZUY
vwdMT8AZLpjjYwt8fG4cnx5EZV1A2IiNlKAd2ZSaeErBbaWcs5TMU0p5l7HG
RFxYRltsZ3ztpS33wsUOXFiJvb1Jiz7MbE9hzLYi4lL6uc24mQryhyNaFwRH
X4KaQOzFCaVXZ2Duv+DhceS6F8g6h9aGI/l/4yX34OPfKfG7QNgGSvF1GP4z
3KuN7FuDpZ+mDSbSc07SfzfHC+9rvLuvcdCevlZF6ZArI+K07m5LmudKzJih
tJ6ptNMcubUP/u7AqE/QWqh2aHrklHhi1YeElZF/6Xob0UzojPjTa0fyTDIu
G9pp0UyZSvd+NeC/dyiLMPY1QHdbAi8t/N4u9fEXK/nvrI+7KF9wBQFbkQc7
NZ7+rX/PBztnqXTfD3nyO8w9Q328Gym9TJtvVRbk0+tvgZ5ECucV2p0Maq5R
mm5TOoOQzjDyoYPsLRyIRoXPoCSHiKYUXhIqzwHyN4j4BVAUotLXgLgYTML/
sYahe+iSMvb/00El/jEnK4GiGi400iarMWEFKq3H5C34FBE2PuGzHeSxCyJ+
LA/hn0fIOYyfOWRTxMUxODdCMkhIMYzJh0kMJ4cwySCUDAPZKJR/P88rG0Zl
g0A2hEsHqKIesjXlRCsYb8KHa/H+j0T1h4y3Yd2NWu/fm7wtMu3vXi8f1pR0
szrrmR+LVEtfaeWna2bFaqcG6kbc1A+4pHvn71XXTq++eHLd38fNTx+1PHbI
4chBr/37Nv2084dtP/yw0e9HH8+tXm6bPd23uLltdnfd5OHi5+7k6eHg6mlv
72lv42lv5WVv6mm71svO1MvB0svWwsPG0sPGysPK2s3S2s3C2tnMymG9lZ2x
lQNBnLGZraGJteF6GyKFrjG1NbJwWG/jYGJrt94mObYvMa43JXYqNaY4Oswk
MnxFWCTlp80OR361ycpSKypkfqxTa2rXau/W6u4jMNQcGNYYHNUcHtcendAZ
4+iMcXU4fELaXL4ul69HginU4gi0eQJNgVhdKNERivUEYm2BTEMi1hSLNAUi
DYFYSyQmvlSXCFVFfFUehzU+xhwfNRgdWt3badTxSae3U3m4l80ZYHOHWJxB
BmeIOtJH62nGmj9QKl8rleeAshy08Cml+ClS/Qo2FYP2KthaiVe9QT5kIHWv
sd5qIOnHp0ax6TFknovNjdMUg1DeQ3ZO4FVio4VIbzZaHwsL7yAv/1F6dlwp
/QTy5grxHcB5i882UP/Xx3j/gG2vSok9yppvxhRlWM8T2nZzYK+NPzqLDz0F
DWFK7/5ZURMGR/NV257pxP6Kl9zGmyLR0UzQ+wjNuwhDN1CSfgNE7TaQwk45
yvplPSVmN/bhGry/BUn8lTmYqsLPZd/aDg45qLSkas5Um7Y8XrXNBPNdSd9m
h6+iImtZ2AYTavpJaneycspZ5Ydn2KJ8E2GJ9QFfppUeo+TOau4z7bY0g00m
VHsNyvOLLP5rU0WVY+JpTXNkhTm+4pQHaAqkTReueXt99XYtiq825fXFlQsV
JkPpa8/aIOcsKIdMkPMOyJPd1NZQurwa8vPoffFw8BGcyAFdCehENn0gAWu6
i/YlsyZLtCcyadynyEA4hZeOiXMhkUtFWWDyHRBkYaIXyPQHoHiPDEbAipv0
yVLG/9OGCd5BeRObPEVSByQlkPseiCrI0W+KVqqihZy+MduGL3QSZTgZRxeH
Sfsjt0bHsIVRbH4Uzo1CxTCcGgbTY8QdxGVD5OmJ6VHimrgAcvKlbkzWD8Xd
mKAD8toBr4060UQbrgVDtehEK/lum3yIKh2hSycwxYSKgkOXjePiYeZom3Jz
ETs/TSfZX+f+WZ3Lx9XOH9U69/uaU7+tPbp//aH91gf2Oe3b7b57p8/O7Vu3
btm2acM2P5+tXt4/eHpsdnff5Oa20dVtk5vrBncnb09HTy9HNy9HRx9HOz8H
K187E1+79T52pt7ktaWXjSXhg66WFi6WVi7mVk4EgyZW9uusHY3NHQkGjUgG
rQxNCdmutXQwtXEwtXM0tU+M70qJHk6N6UuN4yfFNCXGHEpIUg4JxR/cpocF
w9hwJCkGpiVTs5/RCnIZFZWs+gb1lnb1zh71vkH1wRGNkXHCATUnCEMUaHOF
BhyhLldkwBMa8PjaEwL1cYHOhFCHJ9AQCDR4Eg2+WJ0vUuUKVDk8VS5fncfX
4gvVBEINgUj9+5wXFT5fRchV4Y+rCDjqQnKIPEvGZ8l4bCmXJeEyhUOM8TZ6
Zzmoe4d8fEMpz0IIDMsz0bo82P4B66zBmsuw6tdoeSalNR+O1lFFRDrtxxTE
R+sYNjMI5J2YrBUT12P8cjiWh/Q+QxrjkNIA5O1lpWcnlFIPUtIOIy8ugNpg
UBfJ3LQW/GFHk5bQRt+CiWysOgLfYYTd2qPXlsBsDKOU3UAKryPlsepzXYYT
FZql/itaIqgTGfShZGpvKq0+FovajWceRoTPVIi/0ENDyVeVstuI4rkS2bgK
hO2E6X8Dp5XoL/bMikDGUAY9/Ty8tFe3/rlVc8b6K7tZ5mrQSh/daYY++BVu
NAJ/+4K6YFgQoOyxBjFWXXHMGy24jPy1geKkg5rrIb874hW3qC9v0vbb0a7v
MtlpTrXSpsT8DLPOgX3miLPyio26yLNjKD9dU5KnF7aPfspI6YI55cUZdf7L
VYNJNH4O6E6k1D9AWoJQ3ivsUzgiLsRnKvHRdLz4NsYvW8PJZ449hX0hStx0
6kwVPv+RPviSPtusxn2OjySi0+VwqRJMvYVz78H/3Uzrekh99jc2nEufb6YJ
8sHYG3JSm7gKSushuefcDGdaMUUbIJsG98KFfnxx+PuDiRHwnUFyWtPsKDoz
Cr8TR6KnIERcDMPpYTA1TDbBE3fiok6MWIUdkN9JJR2wBnBacKJmnBoF0+NQ
waPO8GkKHkMhYMyIlGdEjFkxe06qOitVneSrj3XqlefoRN/U+etX7YPbjLb7
mWzbYLNti9vWLd5bN2/YsmnT5s07Nvpt8/Pe6u291dN7s7uXn5uHj6ubr5vr
Rjc3Pw8Xb28nL29Hd29H5w1O9pucrDY6mG2wN/GxN/N2tPKxtfSysnC3snSx
tHCysHYkikFzGxK0ddZOxhbORAFobEYwaGFkamlkZrPeytbU1sHMwdXUMSlm
MDm6OyW682HMUErUQEJET0xoekKM6/Pn1Nxcxvv3qgXvWHlvGW9e4C+f4c/T
4PM0NDudfMW6pJBWVc6sr2W0ttA7O5V7epT7+lnDIyrjE6pcHsGUFl+kwSPg
kmgKyKO4WkIJ4YCqPJEKV6AywWVPcJU5HObEBJPDYXG4bC5PmSdkkz0PBWoi
ngqfw+aNM0QTNCmXLuMrTwpZk2Src5VpgZp8gikbVOZ30IbqsE8lyMdXyId0
pOKZUss72FuN9dejnVVYfR5W/QJtzgX95Si/Gcq6qPJuMNUD5J+gpIk8ys2v
wDmFYCwPHcyBnx7BumikLAB9dVXp6V9Kz05RmmNh2DH65pVY+l8qpQ+Q+gjY
nQryb2C511UaIvGGUISA4tUZNPYAiDqIPzmv+vo6lnWOUu8PW0Ng0T+M7GvM
P0zA72tW+G8Ht/ahmw1oiaf0U/419l1HW0lfsV5lxSYTzFwfWusgP9tQT20E
3qvgpT2s/jQNXsHqrFuambcNazONk64bbbZW91tPs9amXNuj/Is7Hnxy9dX9
K1dTlWw04G8u2pVPrJ5cXWOpim4zh5aa6IVtyhPvTSY+2O91UHZWR3+yUEm9
aB1zRH+DHnrUEQTsxc56YL+ZgYMmyCkbSuYhOPZYa7JIm1tgUpto0/7YiP9K
f/gZOpoNu1NwUQF1OA0+2AKv+KCdSfS2O2jbLYT7BEyXwIl0mHEWVEZgnBdQ
/ArK8uFkAZzKQxdKYIU//ZAVOOwM31yicd+iY68ovAIoLAWSSnJ8m7wekGfw
W7DJdjjdSU5mnOuH84NwjtwLJftBESY4MwoU5EpkUaAYArPD2NwwdWYIk/dj
0g4obgXiT5i4Cxd1UfmfcE4L4LYC/idM0kueuFdMYASAUxyoEOAzQuqMgD4j
xGdF9DkJc1ZCn5UyZqTMWZnywrTy0hx7blJfMKrZ2bg6M2n9pT+tt/u5uLm7
efr5btzgt3HjNp8Nm718Nnp7bPZ2JwAkfubj4urj6urj4eLj6ezt5eLl7eTm
6+js52S/0clmo4O5n52Zr525r72ll7W5u6WZq6W5k4WZvYWFvbmlnZmVvamt
k6md03obJ1Mru7Vm1kYm/z+D9qZ2BIOO5gSDvcnRXclRXalRA8mR3fGRTTGh
HVH+BaH3/4yL1s7OBh/KVWrr1Vpa1Ts61NtatepqVSrKlIvyGPmvqPmvYcFb
WFwAy0upH6vodXXUpgZqaxPe+Qnv76MNjzDGJ1g8vioZSokgKtEUy8gWahKZ
pkiiIRSq8gXKXB6dy6HxuQzOGGN8hD4xxiCiqZDPEguUxXyGmEMXjtEIicfp
kgn6JF95WqQiFzKnePg0D58ax6X9GKcFDlSBlregOp1Sm03pLCXf3R1sAZ1V
oDEP1L2gfHqLDpbi/HpM3IzIWiFhhaJGlFcFOR/AeDE6nI8Ov0IHM9Cux2hT
AlISjL65vaI+gvhvBmJ+Z5XcZ5YGKD08TgvbQ3t/Ey26CoqugJKbSnn/KmX/
hb67DkJ3YynHGBknYOQWJP8CTPsT/9MaemkjP2ojCYe0Uv8y+NWeGnaQJXml
M1O56uQG/Acj5rObq98E2QX9qfsm2CgvYu2vPtqaGMV9LUg8CVJPY7+5q35M
XjtdZV0Rr1GR4DRc4vXkzrozOzUPu2uOl9hJGx39D69Uh0jKBR15+brFFtuU
iyv1IEWXqnT2R0Z3otpsqeHLQD1jOgzYpz5dbvyl0/HuXh0nlpKLutJvdsyk
E2v3mVJ+slT6yxZE/gRaE2gz7cZDJQ4vL2oWX4EdUejQEzCcDvvSQFMIuOYG
In7Hh1KpLVeR7lBkMBFM5tMrr6NXNsD04zj/BT5fDsVv8NFUVJqJtEbjh82w
X0zQsF8ZXQ8xfi7Kz4f890BYjIo+AFElOfxX1oRJmyCB4VQbTh5i6iZPEc4P
YLOD2OzQ92Lw+wszikF0dgjMDWFzg3C6G8jacXEDccuguI1wQFzwCXJbUE4j
FLaTe6fTI7hiHM5wwBwPmxNgc0I4J8bnJFRC81LavIRgkL4gY87JGLPEOqk8
N8WaU7BmpKoLU8rL8+wvizoLU1p9rWsSQ2337bBzI/zOY7Ov5wYfb28fdz8P
j42unoQJ+hE+6Orm858P+jh7+Tq5+Tk5b3B22OhkvcHB0s/WgsiiXrYm7jam
zpamjpZmdhYmtuamduaWjub2LhYOLuaE2dmTDH4vCQkArY3MbdZZ2ZnY2v8f
BnsIBhMjPqVEdiZFdseFdccEN0YGlIbeexNy81Honb0JMazMDPR9gXJtrXJX
F7u/X3VoSH1wQKO3R+3TJ3ZTA6umilleSqsoYVSW02qraPXVhLCmWtDejHW0
4d0dtIE++ugInctlCQSqYonGpExzUq4unSTHYUsnVaRSFbFIRSRgCXhMHpfB
naBzx6m8MSAYh4QPiicYojGaaJQqGobCYUw8RpvkMaYF9CkuPjlGk48oEyWD
tA8KO6mjH/H2N7D+Odb+FvRXw9EWMNqM9pRjzW+QxhxK20tksAjjVVMJExQ3
EomUyq1Ex4qR0ffo8GtkMBPpeUrpfIy0JiIVYUq5tyhERq0LRavvUAovI0U3
QIk/XnEfy/uHyHUr3l1DM05SMk5QBp9S20KR8lvw0e9o6hEs7TBafJWd90B7
nyHiv43Ge64ryNc6YI2e9MILzoPGOMZvzujVnWrCfMOBF2aRh5RbH66cql4b
8zfDTY8afs5gmw3DfQ3dgEq5vAt9e5MR9ButKUVH/NH02T0tIyayzwPvSlEf
eqXx7y6qoyF6wpfSFI43PFQL+1Mz8ozxbidoo6308AyeeAr30qMYsJEru4ji
ji3LW518Ya2JstKO9dSPUXrConWxv6lv1VX6cRWyVY9y3h6+uowX3KHlXkDf
nMEyf4ZV/8CeOKziOqX0FOXVcfApGpt4Thl9zpTl04S5cOwpiNmO/usEO6JB
eyBsCaH2JaEtD1DhU6TwAnZvC639IWO+nC5+C4TvUGEB5BcAXiEi+ADEVZj4
Iy6uIydxy+oJGKG8DSq64Bx5hBCbH8QJK5ztBzN9BJX4/AB1rg9XdIDJFiip
xwQfgbgRStox0SfIa4G8RlzYCie7yONOc2QzKHSOA+b52KIQXxRji2J8UUpd
ktEWydc26IuTzHkZY26SMSejz0hoM8Qqo89OsuanVOcn2fNy5Tk5e0mu/nlW
/fOCnmB4VdFLi1uXHLb6eDo5+jq7+JE7MO4b3dwJDH1cCDzdfD1dfXxcPP2c
3TY4O29wcdxIZlFzP3tzbzszDztTN1tTJytTB0tTkkEL4sLe1crF3crRy9rV
y9LZ1czeYZ0FaYXrLKyNvzO43oa0QqIejO5KiulMjGhPjuxIiPgUF9YUE1Qe
+aAs5PabkLs5UfdeRd2NDX/wY2zYqkcp2JvXsKJCualZtbNTY3BAa3hEc2xc
d5yjOzKm19+v19Ot3dnF7vjE6mhnf2pjtrfQP7XQPrVine1YVzvs6YR93fjI
AIMzyuRz6UKhskTMlkrYMpmqjOBxUkMqUxNLVMRitkTAIkxQwqMLJ6h8AsZR
QHbTGkKFA0DYj4n6MckwLp/AieAxOQ7Fw0DcDyV9uLgTE7ZgE9WgLw90vQW9
RXC4Ck60oKNNoLcctOWiTVlIezY6UADGygDhg8KPkFcOx4vASD4cfI12P0c+
PaE0JyL1sej7AMrrK2hjFN6bRS27A5pDAOcVtT4OvPwHlgdRX12Aqb8qPfmd
Uh9C704EXVGM4Re01N+xhwfASJLK0BPWMVtwdQt8fQb5GEU/7AIs1ZV8VlO2
rkNs9JT22DEeHwUZF6i/OeG39lBy7zFObMYT/jXgVzuVPnL4d69y0Dm9Mzt0
t1pgFppK4UfQonDmLifa7xtVtrnS7vwM7/6M77RlvUswO7dd+6ArfsCRlnTW
aKHFrfeNs8cqps0q3G0N9aCn/gZTdMM6pfBf8as/wgOOTDstyl5nNPc8tSVM
K/ua5iZtZKsOZd9qyt0N1Kr7arXBzO7H4OEf+HU7NGkzkv07WnINKTwOCo8j
zf7oUDw6+hQMpNAHEtCeEOT1GWZ7FFX6nFJ1EeafxEZTqMPxuPgZIngKp/Px
b03o5w58uo4uKcb4+Qg3D+UVQk4hyitGBGVAUAHF1VBaB+St+HQ7rujCZnrA
XB85sGm2B851Y/M9+Mz3BonyFrKDgaAS533AiNskbIK8BsCtR0WN2NQn4rfw
/+IrUUXOT6DzXLjAh4tCctzhohgukQO4qcsy2vIkY3la+bOCtaxQWVaoLk+r
Lk4T9sdekBP0EWCyZ2TKCrGyQsZWTNFnp5TnZ9S+zKt/WVjV22wR9cDmjwOu
Pn4udvaejk5EHN1AYOjh5uvl5uPj6uHr4urn4rLB1W6js9VGRyKImniRAJo7
W5s4WZrYW6y3tTBxsLFwtnX2sHP3snX2tnX1tnb1tnJ1MbOzN7UkUqilsbnV
WkubddaEbNfZxEe0JUR1xEe0J0a2J0S2xIY2xARWRt4vCLmVE3zzedSt7LgH
b5NDKh6Gvk8IvBcV4BQbQX3yaEXuG2pZuerHOpWGRrW2dpW+fs3RMU0OR5PD
U+fytXgCHT5fm89bzeHojY1pjAyrDA0xBgfxwX5suJ8+MkAf7idgBKOD+Ngw
PjGKc8fpAq6yiK8sEbJlYhW5RGVKqjItZU+RU65YRPiUEUhycPEYEA9DUT8q
7IX8HuICnxzB5aOodBCV9AJRFxR/wiWtmKSBvHHjZWCgABkoJPv0chsxXgs+
Vod3F6Ct2UqtzyldL9HhAsgpgdxSbJygNZcy+ALteY62JVPqImFNFKU3C+t6
zZxuVRt+yW6Kga2x+KNjMGA72pZKLQ+kE8YX8wOl/DZ1PFeV/1Y16yz+uxFy
yQm9vwEJ+JGy3UzJiq3kq4f8ZI65G6GrIOUne/a/e1T2e6raacOTm9f8+5PR
Gg0lXbaSkYqSuToIPqzanKSWH6T2+LKqqMpqotr+xu/aR3fo7HHUcTSm+Zgx
O165cD/an9qpoovS0m7pSj46cqvtNlkx4YoVl3fRRtJZPRm6e9xY2gz48LaJ
rNa9LmW1tS5uzECu/6Lfm2Hi/wvL2RC5u4P2twe6wxhsW0f10Qdb1iilHKD1
pmj3P9J6epR21oRy1Ag5ZKR0217p7SlG52PikwepuwFG40F7CPrxGmwPgL0x
2Pgj6shDiui9qvQDm5sDJblAUYpPF8GZEmzyDTb9GpYH4j3PaXPNLEEeyn+L
cV5TJl6jnLcopwDhliOSOjKOkib4Ccx0wrkubL4LzpJjZbC5Nny2FZtqAJJq
VFCGCkqgoBzjVxCVOxR9RCcbcUU7leSUiK/DcH4UzI+jiwR9PLgoIKeLEvQR
Wpbi/wH4eZL2RU5fnqQvyxnLUySJnxUqnwkSZ1SWZlSXZ9WX5rQW57UXZrXm
ZzQWZzUXZjVnp9VnpgipLs+rfp3VmpVq9rSvjwp0PLDbydnF28bWx9Fhg6uz
n4erpzfhiC4uPs6Ovi4Wvk5m3nZECl3vbLPW3trIznKtnaWJjbWZk4O9u5O7
p6Ont4O7r72nj4Orj62rh6WTk5mdw3prCyMzC2OL/0/WcRGt8ZHt8RHNCZFN
CZENsaG10YFlEfdyg25lBN14GnEzI/ZOdlJgblp4aXr0x+fxVY+jH8UH/Rob
qp4SuyLzKZL3mlVUxPpQyaxrYHR0sPr6VQaHVEdGVMbH1DhcbR5PVyDUE4kN
xFJCeiKRDp+nyeWoTUywx8boE6O0iVEqofFh2tgQNjYIx4cAZxgKxjARhyrl
0eUi5pRYeVrCmJZQp8Q0UkJsig8nx3DxIBR0A0EnEPdg0n5cNoBLe6G4nSzb
JW24uBYV16CSGsgpBkMFYKQEcKohvwEKmyG3ljpQjLdlo81PYWcmNvgGjBag
Y/lg5DXoeY40J1KqQ5GBTNrIC5D4JzX6T/b9n9nZ58DT42jRA/TtBTzjGOCV
UgdeYQVXGZkXWKOFOqJy9bjDyt4aK3YZrNi1Bj74WTXqtMaPBtBCZcUvHioX
9hse86bnBujNtNtlPdANPKTO/eDaVWDxoxX74sFV0Vc9H983u7iN+qsr8oM1
+Gs7Vh7Deh9nFHdRc6LSq7fMZae72vHN7NZ0NV7FyqsH6HYG+BEPWB7FyLyr
fvZHlct/qNjpwMi/2Id8VHa6q+9xoz27yOa8Xc0vsj7op2ypB/JuKPPy13xM
MflhNe6zjmrMRI640WqiNJJP0zdrIVc9KVlHKRlHsb8ckCOrkPPr0ZAfaGV3
VDMOUnuyqJX3sPcnMO5D0OaP1t1AhW/xyTJMXoxUhOD1D1ljr9X64imjyZD7
DJ18h8py0dl3oMEf+8uFknMVl5UrSwpRbg7gvES5b1FeASb4AKW1cJIwshZM
0Yop2uFMOzbXCuda4EwjpqjHJmuAuBIVlkFBCSYoBLz3KLcIEVYgsnps5hM2
20OWh0TNOD8G5jnkkN8FAb4gwhdF1AUigv6f/ElblNOX5IwlYp2iLRMirqeI
a2XCEJenWUvTrMUZ9tIswaDaEoEhSeL3i3md5XmDpTn9xRmdxRmtOYW2Ykpt
Rq4+T2TURZ0pvmFLlXlqjP1fR932bHX2dvFwsnF0t3XwcbLZ4Gjj62TiYWvi
YrPOkWDQysjWwtjWcr2DrYWLk7O7s5uns4eXk6ePo5efk7uPvbunjauzhYO9
qY31WgtzQ3NzI1JmhhYkgxFt8RGN8eG18RH1McE10f5lkfdzQ29lBF9/Gnbj
SfSd5wkBLx+G5T8O//Asti4npeN12lBGYlFyyJm44PVJkfBJyorXL+G7d/QP
peyPNaoNjay2NlZXB6u3m97XzejvVR4eJKDT4vO1CAYlEn2ZbJVMtlosMRAI
tPl8NT6fzeOxuTw2j8PiTShzR+mcQXxiEHIGUe4Qyh+BonFMzMEmBfiUEFeI
8BkRphCCGSFUcIBsgKgEIf8TEHVCaRcu7cSJwkFCbrzQxLVQ/BFIPwJRBZgo
AqPv4UQpxqsC/BogbMD4dXCoBP2UQ2l9inRkoIOvKAPZoO0RWhuNVIVTep9j
HwPR1xdxIkDaasL7exAif3Y+gRWBMH476EzDh96geffQo07w+hZa/k38xRXW
pS3qvxhhyQeVJwvWSKpMHl9R3mWC18QbKZpck0+rp5+jjmRpJ5+l++9X7Xik
0ZK+6k9f+seHa+Wttu/j9FJurUy5Z3vtsN4qBvBci/5kj4f/ze7I0m3PW3Pm
Z7rtavTBQeTJZfbNY9qVz9ddPah+wJV2brtOc7bjdLtb7L/aq1UY4ZccJ4od
Ey7r7HOE+TexpNPq535UN1FXurYTf3WFnnhGPfvmuh/NcBs9StxRKj9nFfed
0WEXqp/Bip3r4HVv1btb2DtWIUdsQOldlfkq06pb7MdH6HecqTddQcZ+UHAM
1F5BBblQVkAVF9Iub4CXPPHqANATiozEU/hZUFECZwsoA4n43/bYPmMk/y5t
sZE6WQJ4uSj/PSopp8jrgKwGTNbg0/WEsKlaOF2LK2pwxUdMXgWl1ai0CpFV
Y5JyKCgGnALALQLiGkzeRFV8oil6cEU/NjNMNsCf+b79ouCBGT6YFWKz5PYL
nBGDWSlGSobPTVLnJ2kLctr8FH1xmrk0zVhSMJcU7GUykbKXZtgEg4sKFUKk
G5KGqLY8p7E8p0VguDSnuziruzRvsDy7emFaf0ahPjOtOSNXnZlWW1xU+7Ko
Pze5hj++sq3eKuuh5d9Hzbc4mzuYmTvZWLg6mDjbrnOyWUcwaGNhZGNl4mRn
7ers4u7i6unq4e3i6+vk4+fs5efo5W3r5mrpaGdmY73OkqDP1MjM1NDUZI1Z
THhTXERTXFhtXOjH+PC6mJDqqICy8Lt5oTezgq6mhVxPi7z1NO5BVkpw7qPQ
d+lRFRnxNVnJHTmPerJT+57F1qSExsQG7I0JXBkbvuJR4ooXWdSiQkZlpXJd
Lau9Vbmrg93ZSbZR7SFg7GMODTBHhpjjo6yJcVUCSYlYXyoxkEoJrSJWkUhb
JNQQCVRF5HxwVRGXJRinkQMFhgjhvAHIHwCiQVQ6AuTjcJqLzRDiQMUYOjkI
JD0YEURFLZDsS99MDsCVtWCyBqqkBkirUGkFRtzc8feUsUIwUQq4H8hKUFgD
udU4v1pFXKP9/Br99Q3Ykgg+hlOqw0F7GqwNRbvT0OzbNE89cNKbVhlBqwlF
C28hERtB2u+wPBg+Oohe9EKPWmNphyE3jTFdpHt9E37zB1B+g14Xo/z3dup2
K/q7y7SeVJXH/7L3WyJHvZHttqjnWuywB/Kb7wqPtTDqKLMkknltPzvyjCqv
yunDc+O9XjDkuuGVI6t/sIH/7EUu/KwaeXldfprt6X2aDmuxqL/Vh6vM+svt
PMyp3ta0skitiYJ1SZc01qujqbd0OO/MmjONzLXAZktqbui68QqHS3tVjZWB
9xrw/JK2sMylImm1lwE47wsyL8HnZ5j7LOm2bMqtn5RHstZMFlqf9cR+1ENT
9sCOGM2qO1rn1iJn1lH+MF4RvwerD6S2hYLhNDCchGScxHetpsT8Ru2IwTqD
MH42EOdCYRYqyQJxO8AFd1h4hz5XSZcVopISzaYUbU61xfKA7WwLVVwEJIRK
UekHKK+EU1VQXoVOlgNpGS4qwUSlmLgECIqgsIwqqcUnW6G8C8i7CUF5Hz41
TD4xnJ4A5DwmAZwh6cPmJPiCjDovJ0RAx1iQ0wnu5qcZCwrGokJ5UcFc+L4S
1wv/RwSA31PojCqJ4YwqYYhL/zE4r7m8oP0dQ2LVIzxxcW7V/KzB4qz+rEJX
IdNWSDWm5OrySc3padVZ4hfndebla7qaDdOiDQ7tXmttamRjbexgb2hvvZa4
sLNe7+xg7urk6uHs4unq5u3q6+vi5+fiu8HFz8fB083KydHc1tbE2mqdlbmx
hZmR2X8MxoTVx4XWxAVXxYVUxwR9iAgoDrv3LuRmTtDVh8FXU8JvPIy5+ywp
4FVqcO6TiJLnsVWZCU3ZKa2ZiY3pMfXpMXWPoz6mhGRH3D7rf9Uw4PqKqAeU
h3FIdjq94C1eUUZvalLu6GD3dKn0kB3FWQO9yoP9jMF++kA/baifNj6szBln
8rlMsUBdKtGaJGdMaE5KtWUSdalIRSJkSIXUSRFzUqgs49PFE1TBEM7txTid
gNsFBN2YlLhBg5hiCPuvafNUH5C0QWE9JqqF0kZM2ghlRH3xEUoqwGQ5JioG
Y68pQ6/A4BtkvAQfKKDxi0H3S/xT+uqDnlquBljwAVptKF4ZqlQRQKn2p5Tf
UWpPQJNP4rF/qFRHsPKuKOVdpbz6Gz49AvIu07P/AHWBzKcHQcoOrOwfdCQN
SzvN8tKm7DKjbFi3wkZ1xSrain0O6D5TdJcLbrsaP75TNfK60zaPlS6GtH8P
m/g6qdquRPe5Kx/YqHfQG0acXn3nT707p1WGSmx49WbbrLHNLswfHKm5cStF
jRavktS0WfA3T5gfwYi/ZXRml8rR7aq/uMF7h/F7R3X9T6tvMUUy7rHDz7CO
bqe6r8ffBWlz81flRq1yMsZWaSCP/4Z96Sqf0rW22zBcDWiXtmo8vKi33RyY
6Shd/4HaGsqSF6wN3c/2VlvxhyVyyAw5a4NddqVdNgdXLZD8KzTOK3z0CfIp
BLQGUFL3wNwrDEEG6AultPojHaEYPx3lJCtNJCg13qeOpFMVuehkIXWiwk7a
d6Iq0aT+ufHSyPbJjzr8t1ReLoOTSx19AUaIEuAJY+ApHHyGDmXCsdeAW4jx
y1FRLSppArJ2TNaFyXvhFNlbBp0ehrPkBAo4xyM3XpbE/5V+2JIUW5bTvsdO
xvI0c1nB/DxDiPF5Rvn/aJb1eZb9eY79ZV7l87zq8hwRPtWWZojwqbY4o7ag
UFuYUSU1q7Ewp0nUhgSGywuaS/Mai4QtzumQMM7pLc4bzM8bzM0azM7oK+Sa
cqm6XKoxKVWblqkuKTS/LWtMCVc9T17t7aFvbrLW0W6Ng81aJxtjRydTV2dX
d1dXT3dPLzdfH7cNfm4bN7lt8nXycrd2dLGwdTSzdTCxsTO2sjaysDA0jwlr
jAkl7K8qNrgyNrgqJrAs8kFR2N3c4JsZgVdSg64kh15Ljrr1OOF+dnLQm8fh
RenR5RnxDRmJTemxVU+iytIiSh9GFKeEv08JKk8ISAu55eB/bUXAVTTs7or4
EORRHJrzFBbnU2uqaK2NzM42ZncHnciog/2EIZIk9vdQB7rxwR58ZIA6Okid
GKbxxhgiDl0qVJ6SsKZlKjIJa1LClEvocjEhplzEkAnw7zCSr4Zy2wG3hTxk
LenAJ7tJBsnuQJ1Q3AD5VaigGhHXAkkNLvmIi8pQSRkQFSKjOWjPMzCQT6+M
pOXfZQ28BO/vq5zwoVmrI3Zs9NpPrNpYlZq7SiW3lT48QN5foVTc/X466Tr6
7Djy+DCl5CZacJ1SeofWEYtzHtO6U/Gr7uCkJTjtDk750tzVEQuWkstK7Na+
lcGn1rivQfxPqmaH2t/+VaMmVXuh2fbxNY2Ef4wUXb5P7hn8vVu9Ide09o3j
NhvmDj/VfT6ss/u00m/BV7Eql4+vLX9t8/CBzfm96MsoxpWDyn/v1zh1UO1H
N+adU9pF2Xo91c6/bdT+wRmvyzIWNjo+OKdhu5IRdl579INrwDH9Yz4g+Rwz
L0yrNGWNqzH1iB9+/zfmtd06pzep3vlZueO58XyL67NrhuvYlL3WyL2d1Ps7
GOd9NLbpgS066HY9SvKfKl2P16QdVD1hovRwFxFEkc5ItPISWnMF7YqgyPIA
8WXLfdB6h9IZgowm4tIsZCQG5aVC0RNU8lxJmIfPdRplntcKP6DcmKA8WUPr
ToaNIZSqe2j1XaQpCOmMgb2PCPrAOFEqFgN+JSb4CAXEJ2czJm3HJrvg1ACc
GcKJz9W5UWx2DC5OwEUuXOLBJQEgtEhICBZFcEFMCCxIsUUZOb91eRpfVuCf
p+n/6YuC4JH5ZY71ZU6ZwPDLvNrnefXP80Ty1Pg8r/l5Xmt5XntxXmt+RnNW
oTEzrT6vUF+YVV+c1STccHmBYFB7cU5zfk5rfk5nfl5vgYBxTn9uRn92Wm9K
pieXak5PqilkRGTV/LKsNdRudP6wkaX5GiuHtQ525s72Ni5u9u5uLp5unl6E
D7pv9HPfuNF9g5+zp7uNo5uVnauFvauJrcs6K8e1VvZGVtEhBIA1McEV0UEf
YgIrogNKo+4Vht1+FXzzmf/lxIBLCSFXkyJuPIy7m5EY8PJRWMGTyNLnsXXp
cXWPIksfRbx/FF78MKwsJfRdQmBWov+r+AcPw+67BdxbEXgbDbqrFHofifKn
JIZT0pORN5nwQwHeWMP41EKS2N9LHRlWHh1hjQ4yR8mdUtpQDzbcjY12w5Fu
ONoLJvoBEUQlPCaB3rSUPi1lTknoUxLalBibFEKiPJRxyEkEgl7I/QQmmsBE
PeTWk/vY0hYob8MljRivAuWUoPxSTPCByiXfXUR5BSg/Dxl6AVpTGTF/Mn40
oYb/QR3LpfY8o2VdoZ/0xvabMfLurCZMsPAapSoYfXFJqfw2LH0Acv5SSjtA
efgbJfs0JXonJfYHpOE2kL+mNcYxf7cHG7UQLx0k6ojWi4D1Ww2psUeY3HeG
48WuZzeyS6PYU/WOr0L00/6mt6SohJ9TDz7K7M7SfBWid+IH1qdsreocw0Nb
VIsyjNtLTH50xZ2M0e32WMgFzbbcdfWF9pvtgP1a7OgOnfpc8/46q5P7VU/s
Vnkbwmx4YXpwq4alPvrkLq01V+/WcVVDdTT6gjqn2q0809laH/7qTe/NMZQ1
e4ec0VnFwp4FOfS/93wVYX7IBVQ9YAremufdtzGmrTDRVrJWRcKPrJkocMq6
YeirS9lljOZdZsjfsNtijY6YIFddVoS4K+WfBp8i6WWnkPb7COcZOa+tKxTt
DUZEb7HhR6j4Na4oow4kY5zH2PBzrDmJrmjGix7gLy7RZEU0YT46nIFy8+mj
L/DxbISfD3hFKIdQCeRVYvyPmKgeEzeislby+PxUFzbdg033QrIXdz/ZBn9u
GC6MY4scbJmHLQuwZfLpA1wSwWUxvizBl6WQ0GcZ/llG/TyFf1ZQv8zSvxKa
YxL6Mq/8ldAC6+uiyleiplsgyjqNr/OaXxfUvyxofJnX+byg82VRd3lBd3FO
Z2ZaWzFNwKg1I9eYlRNIkjAuLujOz2nPzurMKrRnZwge9RfmVxIxVTGlPynW
lApU5BLtKQnxTc3pqfWBlw2t1ulb2q9xdDJzdLVydXf0dHfzdvfydd/k575h
o7uPt7Obu62Dp629h6Wjh5mtu5mNu5mti4lNVFBtdHBtdGB5lH9hTGBJ1IP3
ZDF4+0XQzWcBV1L8L8UHX04Kv5oSc/tpwoOc1ODXTyLeP438kBZZkhxekBSa
lxyanxLyLin4RaJ/DvEH4u+9iL2XGu5vG/hAyf8+JTQAjQpCEsIpKbHoo1jk
caxSzmMkL4c8jlRdAlvqsb5OxnAvfawfHxukjg/gEwPY+AA21k8f7cVHuuBI
JxzpAOPdGK8fE4ySOzMyHiYX4lMifEpIl/GokgkgHoeSEUzUR+O24WP1YLQK
GymFI8XkdC1uOTZeAofykP6XCOF3RAodeoEOZCKj7xiyFs3I02xHTdRGA7m6
A6uLwpuj0YYorMKf+v4qlncVeXuO8u4yknsZnXhNbUjBC+9ixf6snhyd+lDl
nCPYbS9K8l7s0SEs9FfqT+bQTxMN26s8+Ehlrlzrnx3MU25o/g2VigjWLlvq
lZ8Yzy8yo85quq0BOxyglzlwNEaPbUaO/0Df7ql5dBN2aBt1nwczJ5j1MVvn
8Hb2zYsOScEmf+3GLvxMuXFa+ege1SvnNY7vZT4NZH94vsr/guaBH1V+9wFn
dikHXdAK/Ff1F1/6nRNqUddW3Tmr+7Mr7eF1dvx1lUdBln/4sOMv4qlXseOb
ae4m1NIIlvSDcVumuZ0WdsIDK/Bf2ZBsesyPYaWLuK1ECm8z5YUrB184bV2P
uumsCN0Bc04yss6o3fZSi/tZ480tdn0Ye6aRPpoOOwKpffEoNxMbiYddAZi0
AJfmwZ5YTFHObrhDS9yDHXYCsUex0Te4tITemqQqL6UNZDHe+1NH3tGWOlT4
JRReMeSUAM4HIqjggo+YsBZIG7DJZlzeSgiTtwP5J2S6E8x0A3Ky4RC2MIIv
jsMlDlzmEiYIl0X4sogcS/cdQIzQ50nss5z2hXwGQdgf7cuM8tdZ1tdZ5S+z
DGL9Ns/63wL724Lq/xY1vi2ofV1UJWAkGPy6qPllUevrkvbXZZ2vS7qfCS3r
Ly/pL83rL8zqzU2TNaBcpEYiNqmrmNaZJfdL1WenNBQyjWmpxsyUzvyM/pxC
d1qmK5dpTss1FXLd2el1rx6aujkYWtobOjiZOzrZOLnYeri7eHt4+nh6+bi5
ezo6ezk4eTk6edk5eVk7elo5eFk6eFjYRRLeF1QdHUBE0Pwo/4KI+/mhd96E
3MoJvJHufyX5wb9xgf/GhVyJj7qRFns3PTEg+1Ho24dhuclheYmhbxNCXscH
v0oMfpkYmBP/4Hn8/Wdxdx/H3k6Lvu0fFqQdHEQJ9kdDAkBkMJIUhTxNwjIf
gqyHaE4afJ2O5WXCghxQmgfqyrH2BmyggzbaS5/ox7iDgDcMecMYbwTnDMDR
LjDcBoZayHW0A070kDyKRnHZBGOKR5fzMOkELhmF4kFc0EueZBlvxEeq8N73
sOMV0pGNdL9A+l7D7hdoazqlMRU2phArUhVLL49lPdivfMSPvsEY+BhiCUe0
iu8gOefQnLNobSCSfQJJO6j06m+0/D4cf4vn/EVL+R17G6A+mK8uz9XoTYJn
XZB9hkqbtSnHXBmvb6057oqf90GzztKbIhk3DlBNVFdsXwt8163Qo1LWsMH5
fQZ5Kb8d3Kx665hawRPbE78aXjiiU/bMOCPJb5c7K+aeYWrQ2gM/YNtd0M2u
1MyYNeON1jfOMl0taH6OtHh/3cFGl3sX1KwNlI7s0kiPMe+ssw69uermGb2W
XOPeWqdTvzJvnlQfKrUdrTXfvRHzsmQXPdSVtTiFXVr5izvr8V2D3EQ9X1Nw
7zfasyu0sMN0YzbmbEivi12/3OxRmWhkoa5kq0cJ3gvTTmFRh1W3GmPXd2g9
ubBqjyHct5pScFl9ME1rMI892245lKPWGoY0BVDawkDTXTicBAbiAP8lTfwW
DMVj3TG0mH34HmO4QZ8SdACfyMYGn+J9T5g1IdS/7MERO8qHYLqolDlRhI69
AxPFKLcc8isJDIGoBpXUIbImKGvGCAbJOeOfoKITzvTA2T6y/e/sEJgfxhdG
sUXCDSfgEhFK+eQzwQUyjmLkQ3kCQ8IE5YQPUgkf/DpN/zpD0Ef64LdZ1rc5
9v/miFX1/1rQ+jav+b8FzW+LWt+WdL4t6RL6uqj3bVmPYPDrsu7Xz8RKXOt/
WdL/vKhP7szMrlTI9GRCLRFHQziuMSnQUEi1Z6cIPNVkAraUz5aLNGcndWcn
taYnNaYmdabk+p+/rsvNsHC0WGnruM7Rab2Dk6O9u52zm72bm7Obs7OHk7OX
s6O3k4O3k7OvvZufrauvjbOvtX1kYHFU4AdijXiQF3U/n1DorZdBNzP9rz15
cCnp/oVY/4vRwZfjIq4lxdxOi/d/lhSYHU8o9CWhuOBsQvFB2QkBWXH30uPu
PYu9nR5zIzvyakbY3T3h4UqhwWhIIAgLBFFBaEywUlIkJeMhfJUOX2eAdy+x
kjxq2Tvqh/dYxXtQUwSayslu/4Nt1PFuKqefxh3ECRgJ+xMQPBJG2YmR43W+
d9Ca6IDcLvLwpmQAyobJk2WTo5h0iGw5wmsDYw3YYBXSXQhasrCaZKQmgdKQ
hjQ/Q+seUj5EIiVhSFkEcmUrZqtGsTdE7NaBTbYw7g9W7iUk+QAl/xJ14jX8
cBe+vogV30ELr8Gyu8rVgXj4LnS/BX7Kg/gRlnEMXtqIb9ZGT1nDliiNpdpV
Ty+w7VmUraaUH80pbkZAjbHCSJly6EeDk78abjajFcfqC2osU2/pPL2hwalY
+yjA+OYxWneewcfXepeOs2pfGQ/WrPv7oNqhfWonfte+9ieSEgRPHqAnhmjH
3de+doz+Nlnl5gn6zztVjv6i8Thcp7vYqiB9wxYbPPEOyE7U27+FtX8T8jYB
fxPD3udHd1mPJV+jlqap/LpJeZcbq/WlgaDW8vAOupUe9cYB44K49fs9cLvV
1PzrWFeKWnWsqZUOakBdYcpAbXWULFRX7Lej9mWvnW3cEPab+hZtJPMv0BKG
Pz6MZV5h5F6i9SeBkef48DOsMRgTvaNKiWyfgQ8/RCQv8eK7+M9G6B5TJP0c
bew5k5sCp7LR8uv0ExbgjCdIOKbS8ZQ+louM58OJAsgrAfwKVFAJBZVAXItL
6nFpPSYh1ABljZisGcpa4GQbPtmOT3aRrUdnBshEOj8KFifAIgcQheEiOaH1
v0RKGCKZRb/Isa/T+FeCwRna52n88wztvzj6bZ6wQmXymqCSjKasb/Oq3wge
F7VJEhf1/rek/7/PBgSJ35Z1yXVJ79tnva/LJInL87rftXJxZs2MzEA8ocsb
Uuf0qwpHNeUCLblIQ8pjyXgsuVBtUqwql+pMSddMyVd9mTeJD1tvZm5i7bre
ydHEwdnG3sXW0dXO2cXRzcXJw9XB08Xe19lpg5P7Bke3DfYuG+ycIvwLwv0L
w4n1weuo+28i770OvZERfPO5//Un9/9NvPdPlP+FyKB/o8OvJkTffBR770ns
/SexARmxwTmxQdkxQZmxgdlxATlxD7Lj7hHKib71MOrOjfB7R8NCLCKjQFQ4
GhWKRIVRoiOR6DAkOhiNDUFTopD0JMqLx+i7HKwkl1pRQK0qwquK8eoiUFuM
NJQgLR/Qrjo41ArHurCJXozbB/iDGH8IJxyQ14MR9E2QjSXRiWaM04zzW783
3eoie4/IyO4HkP8JG6vHBirQT3lI7VOkLBp9H6xUHEKpjKFUJ4DyKFAarvTm
HjzshNlqorYr0b2eeNRBNOskePEXaEuitifTHx3BHv0JSh8gxVfQrBM0opB5
dQf3XUXZbojG/YZE7qWe96P6asGLHrDiOq0rnl4YpuK2hrKescJSg/LnZrW/
dunsslNuSDOZKLO9spuVdEa5Io4ZfFLj/E8w6z7txp/YAT809l929DXakZ0q
sdeozyOx0/uVsxKMuz56/3WE4W6Fnz1Ef/9UvbVy/Z978S1u6Mn96nkZVmF3
Vp34kRJzA0kINDn+i9ouN3j6Z9VH8at//YF2Yh8r8F/tvPRVp/exdrkon9zH
/usX1U02MPICmhVE9zHH3E3Z1SmrFK3Ob8NWWWvBX5zxrRYrdtoCKx380l6j
y3u1t1szjFTR39ywj7eYQxlGCUfUjznSa8PonVEg9Xdw3AJ9dZnJzYSjWdhA
ilLDXdCXAgUvsMFYZDAO5SYjuWexgK3484N4XyJD8gybSAS8x8jbU1jsL6w3
95iyRs35ZhonDxW8B4JCICwDokpMVIULKyC/nByKzSlDCfErgbAGShpxaTNO
lIeTnzB5N5wmCsNBnLDCxXF8iYst8wnBzwLsi4gQ/CxCv4jRz2RJSCRS/AtZ
EuJfZ2nfZknovs0z/tPXOcZ3JAkY2V+IOvG/XZoFIpeSoZSk7zNpiASM/1sm
eNT/urSS0Lclgy9LBksLOovzWgtzGouzunNTBpMCg4k+9f4W+nAnSziqIeGo
iSZUCYknNKQibZlEf1q+RsSzObBLb621ubWTsZXTelsXazsXG0c3++8bNQ6e
bg4+rk6+zs6kHF18HV3D7heFPigIu/827G5O6J2ckDvZQTeeBV1/6n/l4YN/
4++ej3jwT3jgxcjQKzFRNxIjbydG3CHKvWeRQVnRwRmR/tnR/i+iA5NjgoPi
ws7HRuyIjjKNjlOPTsSj49HoaDQmEokJp0SHU+JjkNREmByHxkcgceFoYiRI
jkDSopHMFJCbAYtzqVXFtLoyrKEMbSpDm8nT8WhLCdpaSh5/GGjASO/rJAfu
cDpJE+R3UgVdmLALCjohtxmM18GxGiqnFuM3YIJmUvwmON4ARmrwnkJQ9wwp
jVd6c18p87JS9lWlfH9KcRiaF6j05ga4sxPftZ6Wd0f/wx3w4jj2+hxI/gUk
7gdhO7CXNzSK7rPenkfj9iBPDsGcMyDmF2robnjFHX12ClY9oFcGad3ZQT1g
jh60gT9aULfbqLjqM/7ejPVnruaVOV7eofnkokrXY82ndzRd9NFdDvg/+3XP
/GblsxZePK4TdGuNuzn1+nndtHjDP3ep796gfHA7PSlAtyRH/8Jxxr1Lq2Pv
m189Ae9cUr5wXPXGBc0TP9MzUlfFhujt3crc7AUi765p/Wh64Rjj8klm07t1
WakeP3rrpoXqNLzVSo1iH9ig8SJhZXfJ2mM/65zcbfw62S3gvLqfGRp1mvri
jmroOa1fvHQCTq+PvGSz1UFlqyWoitESFpn7/6K6kqa0zQwcs0X/9VS67Ivv
W0OJ/xXm/YtlHEZS9oPWKFpPNBh4BD4FUppuoc0PlAYTsIFIdCAUGYuncB/T
OsLxjhA4noZIXiPcdIriBW38Ee36FlrgQbQtlT5VgYkKoaAA8Igs+g6dKEDH
C5DxYhI9zgdEQL6+SxgiVdqIy5pwWQs22YbJP+FTHZic3KXBFX2Ygoim/XBm
iDZLbpl+f2pPnjGE06NAMU4OtVdMwFkeNiMgH9/PifAFCXVxEl8mAirhjAo6
mUvnicJQ5fv+jMq3RTVC/5WHX8g6Uf3LktZ/tSHB4LfP+t+WDUgMP6/++nnN
l6VVRDr9vKC3OKuzMKM7P62rkOhzhrR6m5T7mqmcPmXRmAZ/RJ0/ringaIsF
BjPT67vb7LduMFhnZ2LpZGnjbGHrYmXvbuvoZuPsauvu6ujlShiio6eri5eL
q7ezU+id/JB7b0PuvQy+nRl8KyP4VmbQ9fQAIoheeXj/Ytzd82H3zocGXIgM
vRwffi0h+Hp80I3HwXfTIwKfxoYkxUXeS4g9kvzQ9dFTg8cZao8zGE8y4KPn
lNSnK5JS0fh4JCaKEktAF4HGhSKJUZQnyUj6Q5CWhKbGIqmx6MMomBqBpkRQ
0hPQN+mg7A1eW4i1fsA+VWMd1dinStD+AbaWYq3FSEcZ6KlEBurgSBM+2kSe
V+K2QW4r2XtZQKgF4zUCLkFiBRirQMcrwWg5OlyBjFahY5WgrxBtfYF+SERf
3P1/eXrrqKjW9n1c9t7Prulh6G5EBRPF9ljn6PHYnRgoFgYgooiAgBLSIN0d
wzDBAEODIoKoKCh20kiHvp/1++7Ned/fWte61xZc/Het67qfu+AHZ5UiTijF
nYUTL0CxJ+DY0yDajih2IynJi94L59iDIifEbTMmv8t4lq3cmm0QfoARuZfe
FZN7FcTtRbz+wM9YwPfWk+KLSHe+Sqkff7E6ZEBCpzdovRLtiHBcdfIPosSL
9TxJ/f5p8pw1GUbJWcCilfPYZ3dxW8RG9ULr3X8wcyIEL8vMT+3l+jryX1Qt
vH1V0+WyhjDTzNNRY9sq1qE9jIwH6tXFM3dtIeYaAx9n5WrJX5fteVtXQ3YH
mUnRi7xctVzOYvJclSvHmRsXAR9Hdujtmbs3Mk5sAzE+nMMbmMstmEneZFYQ
f+tq9qW93OeFRq3FVie3CtxO6AVcUF1rDB1bp9wuMh9+suXqLqM1JlDmeVR4
g+O8ma1PwAb4DF2GkpUA2qgNLq3guywlPP9gFjgTaYeRrANIxVX0Qzbe4AnX
XYUaXZDme6AjAWkPgT9EAYp0X7LQTyngcyrUIwYTleSrCPy8NVito+SxG30e
w/ieDz7SvaPQ+zzkXR74UIR8KII/StAvcuxLKfK5BPlYQgki8qkU+VhG40MF
8rkK+VKDfK5Dvj1GfzTRqw67n6M9r5D+N+DnW2TwAzr0iRj6jA9TueE3jO5b
+4GPdOLDndhwFz5ERbpmQdDoJkZp4GM9JF2zoFNFzuR/RVDl16jqFIUx9ckx
9Sk6JdSYJqMq9U3RcGqcoqHB1Ljh5LjexBiVJ+qMDVN5oubPAbWBfkF/D6WJ
2k8qmC01xPsXvM+vVb90qH19r/71g/rIoGV+6pxZ84wslsyas2TO3CWW85da
LVw6d9GS/9LQZsmCpTaUO120dPGCuzdyfG5med1M9XJNuuOa4Oua7E0R0DnW
w/HB7cvBty7cu+Xg7eEQ4HM5wscx1MvF/57nzeD7p6Oj9ySlLk3LNcgQamQV
amQLeVkFzKwcRmYWOz2DmZKKJydjMXFwSPCMkEAoPACiGBcVBIf7wdEhSEoc
khEP0mOR5EiEYl98MBwXCMcFQEnBUHYULE4FijykXow+KaWPWL2oQVur8Rfl
aEsJeFYCXpSiL0vRdgXeUY2+r0PpZuw6in3IxyrsQxX2sRJ8nD5a/VaOvZaA
NhH0qhC05qPP89EnmWh1LFLoCyVfVQq3VQo9NCPkEBK0j8oBZ2SdgYVOaJIt
knxIKdcJnW+EHF9LxtqzXP5mXttA3t+E1QeQ34uJfCeQd4WTeQnzXg/f3w3S
zjISrnD/NMdWaIM8F35P6eLneZabrLCtlujpNWTEeT2njSrh5wUfSxan3p9/
9h+VikjGwyz+4fWE/wWiMpnv6ahzeT/Ii9Lxu2Pg5axZUWAYHWx4+az6OVs1
Z3vC+wbueEHlqoPy+f0gOVb96gWVo7s0r54ly7KNinL1d21CHY6xbzmrnTrG
/HsdP/2BWX6y6pqlmOdl46wYQ19XVRdb7bN7VVfNImy3MjJ8iTsn8asHdR7n
Wb6uXOpuq3JpO1d+i9EUq3P3tLouAi3XhKx1ocVakJUaafeHxvbZ7HkqM7bO
Qh+HG34rMvT7C891Y9YEIvW+zOYQ7IcMaYsiKhyUGtzh1gd4fzXoKsTfhMNv
Y5Hvecj3TORTLNKZCT6ksy8sgVdpK/nswD/msrqKsB9FxKcc5EMO8j4HdGQh
b7KQ9iy4PRt6kw93COGOQuStFPtQgn0uR6cfS3G6VvgY63qCdj/Del+ifa+w
gTf0qfrBD9j0pBKVD+JjP4jx/76LYrQL7SMoIzoxwJwYYFCYopNBxuRP2oVO
f1P5IGuCisOcieFpDg4rTwzxJ6brFJQjneagxr/4VxCn32qoxFBvasyQZuKE
4eSYwcSI3jhFwyHtkQHdwX61wQGVnh/arx4rP5ShbU+4n9pVvrzT+vxO9+sX
0/7O5afPmJgunGm1zGruUqt5NlZzbebMs7Gcb2O1wGbu/MVW1MdCm7kLbeb7
3Ei745rm5ZrsdT3B43q8t0ustzMlgrHujtHul8Jvng24eS7w9sW7d12uBfmc
iozZnJBunZ5vlFukky9RK5CoCaVU5AklHKGIKxSy8wuIvHwiJ5fMziEyMtGY
GDgkcEZUEBQdAlEKmByDRAfD0feh1AgkJw7JS4bzUkAOxccoODkETgyCE6lf
hUA5EYgoFi7JgKuFSIMUNJdiFAfbqrC2SvRVJXhZjrQpQHs50q6gxA59U4a9
KwcfyrEPZRT7kHdy0CFF39JA3hSCl3noi2zwPAt+mg43pSCPE5GKcCT/NhR3
Rin04IzQXUrRh6AcR5giYMQOKO4wQhnRkwuQLcZw4B7i9p9KPlsY9zdChTfw
h6Fk2XXyZSTjSTzz2Bxko4rSdgMqr1xQcH/J1pnA7zBW7M3O91PfZs3V4sC+
p5Q/lW8Kv77Az47fnMRvFi+y36J1bScWfkPr4Hruse3k6R2o3X7m8R38vZvI
VYvBqb2MyHtqZ21V/D04NSULXK7yl1qj924r11UsuXxB+e8NiNMFjfwcqzO2
5J0bhOdN3p7trNOHmOlxuunRWsf2EkXJmtJ00+N7mDF3jZpLLMPc1cO9LR9K
liSGqfxjwzq4mmEiQFbNYYjvMpuy5nrYma6diQWeZFzYSPxliZ/dt97novUu
G/4CPWjfSkZLhllTitl2M9R2Kf4ynDVcZnB/OzPennwejb+KUH8VxvicCL8I
QWrd0GcxzO4KrS458TYWfR0IdYTDX7Iw6refopDvCXD4bsTeBhE6Mb5m4F25
SLccdJYgb5JBexLUlgS3p4E3WaAjH3kvQT/IwacyQDdUVCFfa8H3euzHI/Dj
MehqQnumb8H0v0IHXtMbLQbegsH3YPgTOjQ9qTRdH8ToNLCXTgMn+4iJAYqA
+DTpaExN021qlDNFOc9h7tQIe3KEPUHFUR6FqRH+FK2DgqlRtakRjckRSv4o
3mnQ1YoRjakRTfrFZmz6vXSUyhANKEyOm02Nm02OGU+MUkzUHaN7vLV/9mgN
9KoM9Kl/7tCpl5NNldz3beqfP2h9+Wg80DuzXDLfxmbhvBUL56+YP2/Z3LnL
LC2X0ksPZ9tQkV46Q+9AXDznzs3kOzdSva4ne16Lv03lgE5pXldSvRwj71wP
871x29/jXHjwzoSEDRm58/IlBsJizUK5alEJXyznSIvZYhlLWswUyxg0ilkU
JNQPpSyRhCkSM4vEZEEhERsLRwQppUQjKVFIdhLIy0CykpDkB1BKJJwbD4Qp
oDANFqVBonSoIBHJCkdSA6HUAKWM+1BuOCyMBeIkpDQLriqAH4vRJhloksHP
ZMirMvRtNfG+lnhfjb0tp2+ZvZUh72QU+5AOCXhTBF4XIO0FSFseeJULXmbB
L9Lh1nT0eRp4mgI3JcAPo6AyfzjrMpR1CTREYLUhaJ6zUtpZkHoGBP6D+G+G
KrxBSwxR6ARC/0Hij5FuK7HrC+C8k6DWA0t3IK21Z1iS8LXNRFu8+neJwV07
zjw+ukQfWm5MBDotuGNnnHmT25amV5VsdPJPlaMbUYftrMuHDKJ9tRwPqSX7
68gzZ53You16Fq8pmhnsa7Brk3JKtEFG3MItfwqOH8Djwvnhwdpn7Dj2J0Bk
MN/xsvIlB8PrF9WFWRoeN/hrFrMcLwryM/XO2rJuXeckR2hcOck/uQ+3P8Bc
t4LnaEfecSTXzkOv2xHiaMHdK4KbJ9TKs6wS/TQ2z0eddhCnNhCzVJCze9Re
iqwL71tZa8Mpt5dMNG6Q3jPSwaEza1lNQey32cZ7zPEd5kj4AbT4BvvYLOy4
OSJ34/TLlXvyyVfByNMgJPk0GmQLWrPVnt7H6q7DrXfh10FKX5LQ95Hwxyjo
UzTyOgr5nIaPlJB9VBpYCHeJ4O5i8psY/iFT6izBOiuwniqipxrrqcV66/Ge
h/QwRd9jrI+eaUL7aID+p6C/BUxXKOhMcIDunEHp7RYd6BA9NogNfcCGP02D
rlPQw4Oj37DRH9MVQ/p9huYmXS78SU7SYNC1+0EaU4PsKcqLDnEmaPxXByco
3o1qTY1q08ngmN4UpX2j+jTvxnQnRrUnRihojY9qT45RptSEouHkqMHkiNHE
kMHYIKWGGv3dgv4uzR+ftZ/XC8rz8dZG5Y8d+p+/zOz6uvS8/aoFK5dZr7ZZ
sNLaavlci2WW5ktnmdlYmCyZZbx4lrG1hZH1TC/XDM/rqR4uSR7XEr1vhAT6
3ggPORGf8Fda1opsoVW+TLtIoSUu15FUaEkrNGXlqtJyVUm5ilShIqMhKFao
yhTKUgVPVq4sLefLK3jyco5MwZaWseQKlrycKJTgD6Lg2Ag4Nw3OTkCF6bBM
iBVNnzbLjoVzYiFRKhBnAGkGXJyNlOYASSqcF4VkBiml+0OZAXBuGFIYg4oT
UXkaqsgGlbmgNgd9mIM8zqerD22laIcCfVeGfaRQSpuZd3KUIuNbEfxGCNNM
zAdtOfCrLPhVOgV6e0xbGniWANeGwBJ3qDac3lmRcY6mYbEbEboTdloG/Ldh
T8KQpzEgch+quI6/TybC96EnTJSuLEDs5oHds7BTK3iLBOD8Kiz7MhF6Aj6/
mTlPi6nHhf3PqrwrNG8WLr++h3FjN3ptJ+lyWPPIBtaRjYLy2Dnt1Qsu7VX2
u0Q8FesHuGsc24UXROHJEcpHDzBjAtnZEeo+XiYO57i7tuOuV1XL5BYhD2Zt
XK/keJ5RVrLoymXl/TtnhEfNuemiet2BzM7QsjvL3raJvHCa4+9hbLuPG3Xf
8PwFFfvD3NB7Gsf3sg/9xT68BbPUY1/Yh1Un6IjjtZ1t+bK4+cLYBcvM4Gv7
seYUw5r42fN0Yd/9cK0fO/6KuhYBbZkNX90AvLaia3SxOWxoIUvpH114qwG0
TxMKPQC+irBXUWjZNVhyDjm/ELFbAomdwFNv0OoDtwdCLwOVvqTj39PB+zCl
Lw/Au0TQV8keaUB65XBHEt6ewuqU4/2PZw40LOqrgnrLkR4F0k2B+qgAXeWg
swLprkK7q0B3NaCJWUcfIOiuR6e5SfQ1Yf1Psf5ndNFw4CX+8xW9CnjwNUaR
cfgdOkSBzg1pDH/57yDhyA8w2jldOuyefiztm26hoTBA0kWKAfbkIHuCIuMQ
f2qIR7vTESpSyqgyRZnSEUr7tCkaTo7pT44ZTY2bTo5TpDOcHNGlXOjkqP7k
qNHkqOnkCAXziWGT8UG9kQGtwW6Nvk61nk6N1gbN0mzG00f8dx2mPd/nhQRS
BFxns271wlU2c1bMM1s2x3TpLOMlMw2XzNRfbK5nbaZvbU6xj/Kigd53YmL2
pefa5EktCkuMihT6ojI9cZmBWKH/P+hKyinoSyuNpJUG0iodaZUuBUmlnqxS
S16lVjwNeZVqSbWKvEpZVsEtqWSXVrCKy1nZQkZIiFJ6ElJcyBRlAnE2UibB
y2VYqQgTZ8GFqVBRGizPhktz4LIcRJEHKnKBIguRJ4OiKCSPEsRApYJQWBKP
l6TjZVloeSZSnoYoUqDyZKXadLghE36SDT/LQ14VIK8LkTdi8FYCv5Ogb8Xo
6yLkNUVG6of58OtcOvt4nYm0pYKWWKgiQKnwhpLIBUm1V4raq5R0HI3dD0q8
0IRLwH0TWRaopvAjAzaDPDu4M5WsvYfvNYaWqyhtUFVKvKz+o8js7hH2bI7S
OjPEWhdx3m+cH2h9eLXg6nZmqQ9LGqJydBPJRcDpbdxnUpPcUPW/rRnRrqA6
TfP6Oe6+DYy71zUpA3l0J+eaPfPMEda+f3DnC9ANR8zxHFouMfTzU9/+F5EY
r5yaprf1b+bFk4QwW+eGI+fMAbWcdOOc/FkH9yMenqp793IvX+HGRKhS//+u
O6sw0/j0YUZsoOrjUgufa2qpMbNjA9TcHObZ71E/v1tphSlydiu3uWD+u0fb
9q0gds8jru4kdy0lVs/TObdW7ZgNbq2NWGiydy5UXWXC1mcoGXIgh03qiVeM
D1tiG1ShA3qwvTEociKqbyvl2inlHEcDd2DyO6y3D/Cmm9BTjxnPfaD2MORr
ARgsw4fkWKMvke0EPipYXeWCD4VWXY/2f2nZ2SKc9VK4cPjp0r4K0F+OdZUi
9K20/+H7NL7J6MMx30vAt1LwvQyh8KMCdFbSa9m66EU0aE8j6G2iV0LRfHyJ
DrT9VxynbSqVKoLBj+jQF3R4WhMppzr6Ax2jS4eURyUmBqcb2GiDyqZBm1La
pk6O8CZG+ZOjAoqAdAvNiPIU/U3/k7Kpk7T2UYJoPDVGGdFZU+MzJ8dMJ0aM
xodNqDhB0XB09sTw7PEhs5EBg8Eevb4utd5Og7YnuqW56ItGzc4vs9MSFi9Z
vX7pujULVttYrZg/a+kcE4qA0+zTtTbTWWSqvcgkJPhyfPL2LNHcArlpgdxI
WGxWIDMTlZiKSs3FZTMlCjNphYmswkxWZV5cbVpSY1JWY1xea1hep6d4qK2o
11bU6SrqqKheVqteXquuqFdT1FFQLa9TKa/jVdTxy2u4xZWM1CwsPATOTEYr
i8kyMSguQsuLibpy9GEFWleKVoiRsjxEkQ8UBaCigF5dWFMI1RbC1flwRRZc
koxIohFRGCyOgOVxQJECKtKhmmzwMBd9mI08zILrM+BHGaCRQir8JAVqSYOf
Z8IvsuFXuXBbPtIuRNpzkNfZaEcOeJMNXqYgT2Ph6kCk2F2pOhCUeMNpJ6Go
PXD6OaQ9ndVRiBT46r+ULmhIUk46hlZ6ESU38LgT8G5LYMWDbE2Iei/mlyyV
ukjNzZaYNjLjz5mEzFflq9SkKNRguSn69yJwahOnMGaDx/lZ5zeTdfGCpzL9
E1vUTm0nb9up7/+Lf+OcVvT9BbY7VdOjNQvS9BzO8SIC9HLSTVwc9Wz3k/du
MTLSLQMCzK5e5Z48ysgoWHAvQPfQYdTVWS0peqa7C+HhyT98lJmVbXrLQ83u
OAj14165rObkwLjlyFy/Gr92gXXvGvPUbtYDX15RgqbjUXbSff38KMPta7nr
FuDuR1Dnw3yn4zppQbM97E3XzyWzfBe8k68ruG+zUBt1OajxVmr1KNZotRFY
oY9JPDS+iS2ST+MbNKC9s0CsLSf7JF7lSTwKQKpdQXsovVTtcw767C7yPhHt
iAYdkeBbFvwjF32bSHr+BW78g4ndsVepvOasmYqYJQ+TF9c/0HuZxOpToKOP
0MF6ZKAG76tGuhRYZxnaSfGxDPwoQyn2fS9Fv5WB74rpaZcqlN4EVUcPo/U0
Yj3NWB99shCjL1ZQ7rQdDHSgPzuwgXcUptn3CQzRvhQZ/oZQ7BulG7lRupe7
Bx/rI8b6ifGfJO1Ih5jTBOROjfGnxlV+jav+nlD/z4Tm7wmNX+PqvyfU/jOh
9ntMfWpMbWpM/de42q8J9enavc7EmO7UuDHNxDHLqbE54yNmY8PGY0NUnENh
ZMhi5KfxUJ9FX7dhX6fp0yr1yiL8/Wu9zOSFy9ass1m/asHqpVYrFlgstTRe
bEERUNvaRGeRifZCY62FxukSi5xi07xik3ypaaHcWFRqXFRmLK4wllQaSisN
i6sMSmv0ymr0y2r1FQ91Kyk06FQ1aFc16FQ/1qhuoFHRoFb+UFBRp1JVr1xV
x6us41fWKlfUCirr+ZUP+TU0OBV1TKGEERdD3xN8XMtprCfrK4kaBd5QibXU
Y88b6PikCjQo0IdyUC9DHkqRRzLwuBg8KQaNUtAggh/mwjVpcHUKWhGPlkaD
0gdwZSxcl4I8yUFaRKBVBtrLwGsF+qoYfSFCW/LgpgyoMRl+HI80xSLP07CW
VLQpGm6OJdvzuSWBLKkHXuGP1IRitQFA4oLkOiDp9lDCQUTkCuIvsdOdOPGn
cc8VcMIpcGExdGwWGrhP1WkDvl4F+PyD3fgH2WMJex9UDTqvfmwRK+AoI9OV
6bqHZ79n9mw9VV975Y6iOW3V1i7HVB22o9tswKXDqgVRWpkRFoc3sjLuCx6L
9e7dmOV9hZSn867aM72cGaJcTY9r/JQkY3d39YtntArzrFJSLXbuAJGhqtnZ
xvv3QHGxM2Xy9W63Lc6dExw7hmcm6Xp6qpw4oXXNfdaWv5Dg+8o+d/g7tnLu
eWoG+AjW2TBO7Ee3rwebFrOyA1VeKiyjPFSdzukc38lZaAFcDvJf5OvVZpra
beRk32C+LTRvSp65yoDpdxR/G6ff8EBjrgb811y8wBF75Kfs9gexgoG4b2M0
3GE/C0E/F+IDpcyXD8h6L/AmHnQkoM+DiC9FZH8F+iULefsA+ZCMefyJ/KkD
Oa1HHwZgtW54lQeSfhwruYl+zMKa/DHZBfhJANYUg3cUoGPPVAYe4Z0K0KWg
h8t+ULz7l4mUAlZMT7vUEJ11dNtMTyPa8wTta8EHXuAD/07Tv0OHP6Ajn7DR
r4zRbwQ9yvRjmmu9+GQvY7KHnOpjTPbScaqfOdVPN61RCSAlf1PD7F8jnF8j
3F9jgv/QBFT5NaE2NaFJVyKmX0R/TWj+Gqeg9XtSZ2pS+9cE9UFBmwL9H8am
CxbTHnVy1HxqdN7E8LzRwVnDPynM+dk3u697Zl/XnO7vFl3f5zeUazWWkcnx
C5f+sdZm/cr5q5fOWb7A3GaOyeJZlP+k2bfAWGu+keZ8ozypllCmL5YbSEq1
JGXaknItabm6tFJVWqkirVCRVajIy/kl5bySCn5ppUBRJSirVimpEpTWCMpr
eZTGVdVRXBNUPqSictVDfu0jft0jQe0jtZoGVQq1j1XrGgV1jfy6BkHtY15Z
FTcjHQizwJMaorWZ+ayJfPoIe/4Qe9VAvG4Gb55ir5vo+3HPa9GnFaBJAZpL
wdMS5GkpaClFn8uxZzL0aRHcXIg8KcAe54BH6fCjVLghCW5MgZ5mwC9ykPZC
rKMYfa+AP1ajn6vxj5X4uxK0rRB9X815XcipCmJ+LeOMPjPMC9T92xy9sQmI
XbGaIETopJRpPyPjLBS1F4nZD4Q3wANb+N4m9P5OLPw4et4MST5C/hDpP45S
3mWOWJFKpiyl3ZbsJ6GGfWVz755StRRAS4yQy7vV2+RbRXH21/cSWV4g6Br/
6AbWzfNzbGbrXD5IlsUz60Tqp3aRl47g3s7wiT0c+4O82FDNY/t5p4/yHM6Q
u/4hMqNVxBINuyPcYB/dvDSdM7bKDmdQRyfOnj0M7zvKvj7qSYkmtY82HDlI
ergqu7ppPnqyI0+0/Ibb2kf17sEBCy6eZMoLzMMDDc4e46THGHleZ6+Zi9nv
gx32oad3M0vSzV+WLrxylDi3gwi/wHC3Jbdbk5f/hp03wle3E+aq5J658LUN
iNM/DFMmNEcZXa8Nn7EB63VR162k/DZe4QpqbyPNUUhLDLslAm9LBO3xSNV1
tNIRbvaDPqXj7eHw2wi0+gZkPxcEH8DaEonWOPJjDt4rQT+moG8isO5CdKSO
VeaAXl0CPLeBp9FIt5x8FgqeRyBvksD7DPRzPpVygu8ytKsM6yzHOmkXCr7T
aoh11gIKlCDSrd1NePdTtPc5+G/J/hU29IbeTUrPVnzERr/go19JCmNf8fHv
xEQnSUWKpBNdzKle1lQfa6qXMdXLnOpj0t/9nN8/Ob8H+b+GVH79t4lU49cY
RUD6ZYaKvyZ0pqH7e0L3P1O6vyf1KGL+mtSieDo1qjlBpY0jepMjFpMj88eH
5g31WQ70WvR2mXZ+Nfn2xeLrl/nvXs2vF6GhQXOs1/xhs3bl/FWL5yybN3PJ
HBNrC72FZtoLjDTmGmrOM9ScayiUGgilegVS7QKphkimKZKrFZWo0k8u5QKZ
QrlYwZMreMVlHEkJWyzlFEqZIgm3UMQuEJJ5QiInj8jNYeZlMfLzWAX5HJGI
LSnmyhUqZZWq5VWqFbXqlXXqtY/U6xo0ahs0Hjaq1j9RqaznCguInFRQJyfe
tOBvXjDbnzLbnzDan+DtT9A3T/GOFgrEmyb8dSN9v7i1Fn1WiTwrB89KsRY5
aJHBLWLwrAh5LoJbC0GrEGktgFtz4Zc5yKscpC0Pppznm0LwTgzeS8HHYvBF
ATokSFkwmXGFcXo5GXOZ+TpN2XUzy4yNmPKgFbpo9AVV4XUi4ahS6ik43QFU
BuDtaYTIFc+7Aqr88BtrgZ0FlG6LtfqzKm+RqY46x1exDNEZp2w4VR7sF/Eq
4Y4qBnx0piqRdUvQGqPcmKVz/h/WpsXEHB3k5BZmk3S1JGXFgT/Zd6+w7l7H
9/zNtN3Fc71q6utmVJSlXZhl6OQgiA9XlxQYOZznO5xCb17H/f20iiUr3C7z
09JnZqUZunloh8XNu3SFve4vKCDINK/AyMmVHxaq7R9kIxKZObtgJ09vTkzI
OHvG+vJJfogP/8RR3Pk8WpKsGemrfvGEyr2b5nvWcXasZqd5M+UJWvev6f2z
grd7Nb7ICN63eWbqPSunAypzdVD349r3T+utnMnUY8DbFgviXU1c9wjmsSAL
Buz+N7PlAVZyC8mwhRMOYy8KTN/nGrYnQ8/DkConuNZVqfk23BoEv/BTeknh
PtJ4n2iPANILaMCf6MtkorsAtIcjn2Kgz6loeQDr5mb8wp/Ejc34wxDydSJa
64pVuQKFM1riCJVegyrckFof5PF95NkDpD0FfZeDfi7CvsnBjwqsu5roqqas
KdJVj3ZND1n0NREDlDK2oIPPwc9X6GA7Pj3lBEY+YKOf8dHvxHg3Y6KbMd7N
nOhhTfRxJ/o5E/1sCr8G2P8Z5P76yfs9qPx7UPD7p/KvQd6vIYqJgqlB6lt5
akhlalhtcrqh9NeYzq8x/V/jRr8oFzph+GtS/9ek7u8pOlLqOTmuMzFKZYVm
E8OWk8OLh/sWDnTN6uk0//HZ7Mt7y8/v5jeXqFy+NGfRH2sWr14+b8WiWcvm
mi6ZbWhtrrvIVGu+ocY8Q7W5BppzjaQ1prIaY1m1IWU+i0oNCuU6wmItoVS9
QMwXFrELxRTpGEVSVpGEUyRmCYuYQhGH4qCwkJVbwMnO42RlcdLTGCkpRFIS
IyGRTEggkxIZKamMtAxWZiYnJ4dbIOSKxDxZCa9EwS2r4JVXccsruBIxKzcd
k2Wjj8vJN8+Yb1tZb58xO57hr5vxN02s108IekqiEet4gnfQl46xNw3omzqs
vRptq0Bb5egzKWgpgp8WIM/ywItc7EUOoIuAmcjzdOR5KvIiBXmZDrdlUEDa
M5A3mfCTGHB7G2mpis0WYL4HOGJP7PZO9MxyZJ816rVPXeLGoQclbOH4I1CW
Ayb3BL7rcflVvC2WFW7Lt51DXFqCnV8EvDYRbYl6rzKNjq1kWSorXVqHnlhB
7J4vSLm97K69sdM/grvHoRN/AS97teBbJtvXqzkcIktjudVCvXOH1OwPCk7v
VTm8iZP5QKWmeO6Vk6qBrlxJGufyRfLWFUZ2Jvf6Da6vr46Ts+DiRUZWioqn
G9vNlZeVoXrTjZNfeF4oWn7OgXf0hGDLDiWfe9o1VRY33TR27oUuOquExPy5
9wDpf09DLLP0vKV/cJ/axVPsa/bsozuJaH/txtI1D/z1zx5WdjuntmWV4PRO
XXmKpSjZbPdy9PpBnc+VS8pjDHfNgxVRpj0P1wbacfU5SNAZtU+ZRvUR6ruM
ged+XtplRt45JPYQCFg/w28zKvHmvkjkN92jjCXS6IvUusAPb8Dv0xmf0lB6
C2IE/DUVa/CCc4+h1R7o+2TkHSVzwUofI0DaYfTySpB1C++uUWnLYb1KhN9n
wu8ywet0+FUK8jwWaY4ADYFo3T1Q7Q1VeEAVnnClN1Lri9T7wfWBcGM4+jKJ
+FTEpDxqTx3W14D2NiIDz7CfL7DBV/jPN+ggvetp+nX0I04fGfmEDtL71ojR
H8RIJzHWSUx0ExOUQe1nTf5k0iX7QQ7dLTPInRrk/h7mU/jPqOD/xlT/b0zt
/8Y0/m9c+z8T2rQppQSRwigVKTXUnxrTm/y3ZE9X7Y2m6xRGk2OGEyOmFA0n
hleMDa4cGlje37P0+7dFb1/O93QxWLXBZtG6FQvWLJmzcr75UkuTJdNGdJGx
1jwDzXkGGtM6KK3RlVVry6o1i2u0S2q0S2s05ZXq0jJ1kVy1UKZcIGLl5OOZ
2URGBkkhO4ORk0lmZ+IF+UxhIVsoZIqKWIVFrAK6Os/NyWdn5rLSs9kpmeyU
dE5qOjctg5uWyU7PYmflsnLzWXl57Lw8Zn4BWSgihIWM1GQ0LhTOicZrJJQm
kp/aOB9ayffP0Y4WrKOJfNtEvGvC3jaBd43gbQPytp4C6KgDHbXYmyq8rQx7
JUMpKXyRi7ZkgafpoCkZaYyHH0VDDyOg+gioNhSqDYZqg+D6IORxGFIdBjwP
4PNUYH0YXFqLVwchjWHIYz+i7BaSfhqJ34fmXEAj9yv5bkEDt+F+f8Iljqjs
tlpnucH1Xey55IyVHKXgXaymAOWHwRr3T3BWzOSb8ZimytCDyzqvktQ/yRY5
7lU3FagsNwNFAarvS41FCXprZhFuFwS7V6GHtuDZ4bxq6cJLx9U8r2BpkSoX
7PhH9zPveAtsD/DO2zEdnZl79hDRwRrlCoNrTqTTFZ7zdd6BI7zbnsr25wlH
51kurjq37+kmZyx19dS7eIWICGF5+QsOHeXmFq1Iz7U6fpyMCGTHRapevayS
lWOXkz4rIVj3xknVM3vx2xfIq8dZkiRDRZ6V+xXL7YuZhYEqj7LNd6+Cj60n
kp0Z/vacdWZo3CWsIsTw1EqmBgHuHcTFziy/vdzds9FCJ9aTQE6uHQjdD9Ls
Qcg/aPJhuCUSrXHHWoKhTxlY4w2k4ToyUEn0VqCvgogPKdjnAuR9Knh+F/kY
CzrT4XdhUHuQ0vsQJHI3dmI5KPQGrQnEgAL9VoB+FWJfRHQL9xcZ9lmGfpGD
b8WUF8W+ybBPUvBWCNoywYtE9HkceJWCvy8gviuwnnqij0oMn6D9zUR/C95H
v45iA+34wFu0vwP0v5nGa4T6HnyPDU2XDke+gZHvyOgPMNqFj/ZML1vrI8b6
sPH+6VbS6Yn7yQEWPXU4yJn6d9JwWPk3hVHBLwpjKr/H1f4zofmfaVb+h/al
ev+Z0PtN1xD1f40Z/xqjaGg6OWpGq+HInPHhRWNDq0cGNw2N7Xpevdhm7Vyr
P5bNXT1/9qq55sstjW0sDGgRNNFeaEhxUMvKQGuuIYWCEvWich1xuZakQpPK
BGXlKsXlVBrIk5azZOUceTmvuJwjKaVcKDtfxMjKxzNy8JQ0MimJTE3EUpOw
jFRGViaZm8ssyOcXFvKLxGyJlCuR8UQSXoFYJb9IUCARUFwuKuZJ5MpSubJY
xheJKUllikREYT6Rkw7iI5TCfaHkQEyRT7x6zPrQyn3/gvmmmWhvQF8/Qt48
ojiIf2wkPjUSHxrwd/XgTTXSpoBfFUNtEqStCHkphF7mI6254EUWaElDmhLh
aSYi9ZFITShccR8uD4IrApCqAJhK/ZKvokdX4LZW7EIHMvssmnIcNIbBEics
xR6r8CUD/kG8V4OHYay2DDLmNHFqFTPkNKPISSfsOP8PDaVtM/F7u0jbFfBi
DVDgNUsWbrTOFLP7A1fcIYPOYLbreEWJLiE3twaeUcvwZDvZoqe3cIRJphE+
FrY79GN8ZwvjVM+dJI7s5Pje5p/crxLgxpcXGt711rznwygpNIpJ0DpsC265
891vqmRmGCQlqN9wUy0us0zN1Hd0YfsFm1+7YVhb/3dekdbuPfA/f4OUdGOx
xNLFWfOiA7ZzF+PUKeLyefVjB3iRAdpBtzkR3rrZ8drXr/C2rGLvXCtI9CIL
opWdjzH3rsf32CB7VzCcT5hdt9NbP5vQ40C71ikHH+ccXgYMBKg2AVYZoH/q
oSsNkdX6SOA2VHodDdwMYs/gzzNAhTdRcR37lo3V3yGaA8m3iVB7At58D38a
gNS5ItVO0Iv74F0K8q0Aa4uA3z1APibC3zKxt2Fo6nFs90yw0QTy+Ac8i8be
JUBv4qDX8dCbROhtKvIuC3mfBz4Kkc/i6RH7IvBeBD4IkY9C9LME7axA++qx
gUbQ1wh6H+M9jVjvE9Dfggy8QPtfYP1UpBeYgN6XoL8NG2ijzxf20+3cFCtR
eg3+e2zgIzr4GR36ig79wEZoJuJj9HDT/2qF/3ayURimm7ppJg5OTx3SDd7c
yRHu5Kgy3VBK+1L13+Oav8e0psmo/XtM5/eowdSI4dSoyeSI+fjwzIlhq7Gh
RaODNoMDS4b7V/X3b3F1mWlkM8d81UzT5RbGyywMllAENNZeaKS9gOaghhUN
zbkG8anc9HzlPKmqqFRDrFAVK/gSBV9WzpOXU5kdp6SMVVrBnAa7pIJJ8bGY
4qaCJZazhJSfzGekpeOJCVhMNBodSQGLi8GTEhhpaZTw8XKFgnwRXyjhS0qU
yypVyqvUKqqUy6u5ZVXUn2WXlrLLSkl5MSkpIoTZcGKEUoSXUrQXLIwDT8qY
r58w3rfQUkhx8M20/L2pRTvq0Lf1aEcN1l6GtMlBmwS8EgIqGWzNQV7QRhRu
SYGak2kONkRC9aFKtcFK1feVqoJAdTBK8zEIFHlCsYdRv80g7TgSvkMpfj/o
SEfTHbAj87CbO8hdxvBJM6WondjLNMJ9D2rFhR2s0ZYg7qcMdY8d5DJVZOsc
rj6YcWQFqyWI3S3SibnCMFIGp/7QXGNGXD+i8jTD4FuFjf8V1Z3LBeZq5KE/
UUUs+2X1Yi/HuReOLr7vY7p9Lc/zKrciXys+Uv/6Bd2cB/x7PkzbfeBBGBkU
zLp2TdPPX+1egODubSIrlX/qBIgKU0lJ17txm1vxcGVwhH7wg1kuN3Evf/0T
Z9gpSaqFhabnL5GhkXqREUaubqolikUh9w3/XjvjlqNqgJtWWhg/zk9w5jjP
yV5l75/Yjj+wSG/10sxZDntYc424GQFm7aXzfB2UF+qTQn+TN7K53nZsAx56
dqdGUaCRwyaOLgYZ4MhiAbTbDP5bE4k4xWpJIdMP41J79Hsm0pGEt0YQj32R
D1LlwRq9V3GgPQE03QNPbsLPPJBPafC7aNDqA72NRLoKGaF70D/UobVGSm5b
saZoZpcY+ZQLfRehXwrB67QZbVTikIK0piDPUpCWJNCSCF6mIe/zke9y0FWO
9dRgfQ/pSn0vfb4Q723E+pqwvmail4pP0b6ngK7dU4LYgvdON7b1ttKboHpf
YxT63mAUB2m8Bz8pa/oVHfyBDXWi083bxL80pEGvv/hfI81P1ng/c7yfNf6T
M0Hvg+JN/OSN/+RO/ORPDv7bVqr277vNFF3ImLapYzqTI3oTw2bjg1ajQ1Yj
w/OGh5YMD/0xMLBufGJdUba14SIDo5UmRstMDJaa6S020VlkQIvgfAPNBQYa
86e96DzDW077/fxnRsaoJWdyMgu5eRJlkUxVXMqjtE9SwpTIWVI5U1bKKi5j
ycuYJWVkcSkhLyNKysmSCkZJOaNYQUhlrEIRIyefSMskE5PJ2AQyJpbxIIaM
iCLDIvCICCIujpORoZyfLxBLeKUKTkU1t7pWuaaGW1fLqq9h1FWTtRV4VRla
JgGFGSAtEiQFIGn3QXYIkMaD6hysqRh/VUUREKPwrg5/V4u9rQQdZeC1DLQX
Ia/yAc3BDORZGmhJAU+T4KZ4KgGEnjyAGsPhR2FIlR9SdAtKPg/CdlNuExd7
8ETXQOxhKGorWnETU9xBfLfAl6yV7Kzwe0fYceeQ6P0g4yJw+xvYLUK9VoKi
C1iqPXZmGRpywqgpcd6BpawVGkjsGSzmLL7JEuyxZlfG/RF1Y/7xlXiBB5rn
CW7ZaQY66cqSjPyvqd+7yLxylLPeGrvjxGyQGKY+MDi5ixV+h/DzYl84pR/h
rxMRZux8SS801NTtltqVK5yMRLU8ocDJiePuwbp2kx0XZRoYZOJwQffuXY3Y
1DlhsfPtLzEkcsuwWIOLDuD8RWBvz0pK03BxYjlcUE6I0omPsQy8Z1lbtSIl
dua+Lej+LcQdZzIvTsPRjmtjjt51ZlYkaXs7kJuXkD72ZO49Zaf9rHVWrKBT
ZGWomsdhdK05nufKbk8zyXBizVGGzFXB1X/4Xjv4203gfUaknSV6ZrZS/Fb4
ZTD6KQN56EHZSyTjMvlRqPImGXkWChQOSM0V+MktpVf3oad+8FMfpY4gJOwQ
esAcubMDF7ng3wvwr1no9wzkUyZBT1JUG3c+Mvgsh98V4W3ZoDUNeZ0NPorA
j1LQXQG6q5CeOrT3Ic3BHgqPsJ4GrPsR2vUQdP53yBfrnR5uolfQvMAoU/rz
NT3TRJvSt0j/OzDwARv4jP/8TCWG6NA3WgSHu/CRbpJeedHPnBiYbiv9d6p3
mK5W0PX6UR4lfNMd3fRCtmnwxge4Y/1U5I3SW4K50+CN/eRPDKlOjKhPt3ZT
vtRscmj+6M+5v0csxkaWDQ2v6v+5fnxog6ebqba1sfFyU8NlxgZLTfWXmOgs
NtC2NtJcZKS1yEhzIcVEQ835RhdOejmcdHE6d+j2zTn+9wUx8cyMLHZ+IeUk
+aJigbiMLS1himkwpHKGREaBFEsJsRQvEhMSKSktxqXUD4tJcTFTLOeIZKyC
IlaekJ1bwMnI5yRlsB4kMEIjyKAgMjQYCw9D42OJtBRGbja7SMQpkXHKSznV
5ey6SuajavJRLdZQAxqqsboSpCwPCGPRdH+QfAdJ8YKy78KSUKz0AahOBA2Z
aGMO3pgBmjPB82y0JRM8TUWeJiAtCaAxBjwKA7WBoMwbLnaHpS4g3wFOOQFF
7FTy2TjDZxNSFswceCaoj2FFHUYLzuPP4oDiDurzF3L3LyhgG8i+hDdEgxxH
KHATyDyLPfLHPVbDx0yQdVrIAgFccIXsylFvjlHZsYC0UiN2r9QxYM4Isddp
i+a8LdCzXUU679Y9ul5r6WxW8i1GSza3Ol330EZBwJ0FZw4LLh9kFz7gZcSq
7v+HedWeGxGsefaU8l13UpKjFXxfPzlOVZqrc+++xmlbxNOT73PPOCPdXFGk
GxbCjIy0rKjZde4S++Zt/br6dR53VEPCBS43GckZmxOyVx07ynZx5R4/wnNy
1gjxEzheZLtc4oYHUn/T3PWa3vGDTPsDzMBb5E0HTc/rs07/wzz8J+p6Ti/B
z/rsXywzVXj7Gna0u8Hpjcz9S0gLTVyPj59cDSVdYZ3fiJnykDMbOE+i1N6m
qN7fCa3kwn9pKx02QWP2g9KroOY2JruERO8GyWeQV/F4awCoclSqvIRUX4Ea
3KGXgaDlrtIzb+TlHbTyJlnliz0LxdujEakL02sD494OMvggqypU/VPjyt7n
ez9IWB+E0GcR+C5Fu+SguwzpUsD01t8KtKsS66pCf1QiP6qQzirQVYt11aM9
9GsMzT66W+Y5oNjX+5wG9dHXSk9Y9LyigPW0U2qI9nUgfe+Q/g/IwCfw8wsN
ypEOTzvSkW5stIcWwfEBkjalg8zpxRfTZcRpTA3z6DY2iob9nLE+7lgfZ6iX
PUTfquAN9/BHetVGelVG+1XGBlTHBtRGB7QmRmYOf59XU2Lc9dlqamzZxK91
j8vnLVipq7vCVJ+Gid5yU72lpno2xjqLjbWtTSgmai0y1FxoqLmA4uDNiyed
LtheuXjU2eHYYcczKzxcjSIi+KlZnFwRq1DCpqRwmoOktIQsLqFlUVrMkFAc
LMJFhQyhEC0owAuEjLx8Zn4+K7+ALCigcj0q6eMJxUyhmC0U8QtEgpxCbkYO
NyWNk5DIiU9gxcbiCbFoSiKemcrISSMLspmiPLxYhJdLiZoSoqEcbaxAH5dg
D6WgXorUFABFOihJALIoWByKiALRwrtovhec5w7l34Ly3OD8G3D+NTjPCc65
jGQ7wDkOcPYlOO8KJHKGxNehIiel3AtKSbZw8HYo8Rxe4ccNO6e+UQ/z3Uko
vEFtAJJqh+dcxhIvog4W6P0daPQpNHgHiNkBWmM0nqXouWznWDNn2LDh0ANk
jS8achJfZQR2zOM3ptkk3F556g+9nJvcu0ewlWZ44Hntp6LFYW4LT61XDnEF
R/9Qcj6lX5mq8bzE2PMa99guwslOzW4PJ8iLVSM1iAxWPWdLBvjAl66yL59l
RfrhPj6Cm+46GWnzCoTLPW/rJUbPue2rcvDgjOwCi5t3NI4dh1Mz9O8Eal1z
1Ha9ZfLk5cWQMPN7fma1jw5eu8jx8UDLivTu3tE4dYyx+09oz9+oKNuwUrbQ
dh9jhRU3LdT4WdXCGD99m5lEuLv+26p5eZGqay0J77OqrSJNeZz6SgvizDaT
W7Z6c1TQ+WqoIQnUEaUrf7OLXYl6T9bNNfAadaWLK8mc0wzJJaTWC2+NJZuD
4Fpn0B5KfssAD29A1U4zHrlCjR7wE2+l11HgSyr+whdp80c+xiBP/eHSa1Tm
iD2KVA04bixP2NaQt6viPqs2Vv1pgsW3IvZ3EfxDjPyQwj9k8I9i9Ecx9l2O
0O1qpYBevl2JdVZhXdVod+10B+ljShApJoLpwv20FD4l+lrQ3udI73M6Mexu
BRQHe9unvehbOh8c/IgNfSGGpnfjj/4gRrsIin1jveR4Pznx/2+eGeT8GuLR
GOFPayJnerCCnm+il7ANCijhG+mnCMgd7OYOdnIHv/MHf/CGegQjvaoj/RQH
NUf6dabGrGJCLNZt0bxyy8LTY8GGbbo6q0xNVpsbrjQzWEnR0Fx/ubn+UhM9
Sg2tTXUWUzCh1FCL4uDxqw7HXC4eu3jh6PlzB+zt95w8t+fYJdtN1y9b+t9V
TYhn5uWxCovYRWKWtIQlK8VlpSTlS0sUpFxBUB5VLMOEIjQvH8vOJjLSieQk
PD4BS0wi0tJZ2Xk8in1CEa9QxBJLOVI5XyrnyUr40mKurJhXLONJ6McZbqGI
IxSyC/JZBTkMYRZZmIkX5aLyArisEK0QYhVCUCPC6kXIkyLwVIK1iEGLGKFi
cyF4nIs+TAe1SXBVHFQZA5dHwIowRBECl96HSwOUFP6Qwk9JcRcq9UZk7pDo
+ozMs1C+MxZ6FDtiSc7igwUc5N4Rg8oQ9VQ7KPs8EncCu7YIvjpXyWs1UhvI
LrpJPHyg+6nUPOIMz2uf7uU/VP7SA3bLsGW6kAaq5L6d/yKC+aPELOw0b9s8
7u51OqvNOdmemi8zVRvyjNdZYUe3zz+yZcHupWjMDVAQybp4jH/rAl+ayS/O
n3/rimqAOxYcoHxwp4q3h2ZausGN26pXXTTuBxgHhwkKsmenxGgF3Dd5kLTA
L3j5VSdTbz9Dbx/zwAhjD19jVy+V2qYNRSW7XN04R47MEJfYVpT/5XiB63QZ
D/QWhAXqF2ZppCZrHNqNul7ghfkbXrrAOXdI1/8aK96bG+GncWIf69xWONJF
JyXQ9OoRXvg1rQIffsJNtu2frNq4OV+qF6e5a81Uh1QJaK0Vf5UWdnIR5rmN
uVwAbzbExHe4Xwu1y13wWjekU0L2lpGvY4h3CeBLPtYUQNQ7KzVcQx7dgh55
QM/D4eE6zsdMot4La4/AGnxA5nHQFIy0prLe181+V7OuOdG8zo8eZfqYCn7k
wd8LkO9C5KsIfJMgFL5LwY9imHKknQrKlKJdFAGrAEXAnjpAudOeepyu1P9r
TWlHCnqaKNCnRbufYt1P0a6naOdzCqCzFe16SYNSxu520P0a9L4Bve/A9L5u
euJ+6CtBv9J0U5T89zQMvSuYUr2JQdqOTo1ON46Oq/2e1Pw1qT01ofVrQntq
XJPyn2ODqiO9yoNdvJ+d/J9dgoFOwVCP+nCv1viAwUiX1Z6DRiqLtPRsjPTW
mJn9YWK0xsxopZnRCjPD5eYGFA2XmenamOguoTmoTXHQmu5VO2d75cKxS+cP
Xzh36Py5/SfO7D52es9J+4OX7A9dO3Xkoq3d1nNOhj7+7MRERm4OSyJmSySU
/2QWlxAlVGJYToE5PR/BlJYyimSsfBE7PYuIiwcR4VBIMBQWgkZFEPHxZGoK
kZXFyMsjhUKiqIiUFLGKJawSGVlSwpLTjzPMCgWrQsGuKGNXUt9ysqKYLJfi
pUW4LA+V5+Bl2WhJJlyWCVdlI7U5SH0u3JCPNNM3zpDmHKgpC27KQpoy4MY0
qCEVepwMP4qDH8bAdVFwTThcGgRL/dBib0zsDhXehMTuSPpFOPQ44boRhNvy
ywM18i4hCYeh9LNw0Db49hro1hKozBPJugGfWUM6/0GknMZbQ1W/51uku/KX
66LmXFwdgQ7boDmXiaTL5GZLcHKTypNki6aspZFXrYLPM/esIjYuwoWRi16W
L0wNm7lno8rlEzwfJ/3LB5mJ/rgwkXv9isDNkZUQqR4UyPNwYRSms+77Mt3c
NWQS87gY/rXLKtFhc3KzrPKzrd2v6xcWnCiU2bh7CXIL1iVmLvP01C0rXxIV
rebqxi+UrhIXLXW6QPrdU85L14mPEFw/R3rdBJ5ujJtXda9d0d2+CQu/y68T
L3K2E9jMhu86qRenmQW56a+0Ylw8rC2KMfA4w56tCaz0cLt/VBLPcR7HaAXa
MYyUkasHLZqTrKvDtXfNQQ2Z8GwS3mMGNafze2qMsy8ycuyRei/QGgla45Bv
IqxThtZ5orU30JfBoO6GUv1N+H0yWn8HS9kPhWyE6v2w91m45Bqz+AoScxq8
L8Ar/VkP787oSIQ/pMEf0md8TIc/Z8Nf85GvhciXQuRrEfgmBd/k4HsJ8kMB
6Ka1avRHDUbvfarDOuvpLYjdDdPbZp6gPc10E2l3C9ZNxad4z3Os5zlKx1a0
uw3toTfkI//mhv3v0J8f8UGKd1/wQUoQvxKjPxhjnYxRerKeyg25Ez95E//d
yz39/PJTeeInf6yXO9zFHunl0JcpKCkcVqNnDMe1fk3q/J7Spmv0Yxrjw1pj
P7VH+3WGejWHBjR/j5l+eb38r63GhqvNzdabz1xjYrragvo2WDVTf9XM/3Jw
man2UjOtxaaai000rU00rE0unnA6b+tsf/Sa/ZFrdocu2x66euTwtf1HnHcc
dFq/6/y8v7YarVg+e7Xphh1aJ85peAcIYpI5ufk8iYRbLGcVKzCpgpRSOWMZ
KVNQZOTJynlSBa9QysnOY8QnYhGRiJ8/5OsL370DB9xFQgPAg1CQ+ABNjcUz
k9CcNJCfgQqz0aJ8XCrESopwhQStlmMPFfijCryxCmuuRpuqQVM12lwFGsrQ
Bhn6WIw1FtLHBJ/kQi250Is8uDUf0DEXfpGFPMtAm1OR5iSkKR56HAc1xEF1
UVBTOvnlsVaSm8rdI2iBGyK+qpRxFiq5rlTtCRReiMgZTj0KR++ekeOAh+2A
Q/eA4F0g6yLpdQDMU56xzwoE7yArrxJP/Em3rWjAkVkViasddmhtns3eY81a
YTKDO0Pp6mZWfRDnvXxe6GXlfau1r5y02LdKOfQiXJuIpvjyt67mRLlrt0gt
4gK0rtsz7t3U8LlhcPUkmRTOFubyT9pjRw9D4SFro6J3ud7Cbt81u33LODJK
LSF2UUjgLNsD6iEhGxNTjQ4fUbI/BydmzgkM2+7kLDhznuHoyBHmmpSWGZ2/
yHS8hKYkkV5uDH9P9bjImS6XBA+CuaIMFYez+PkDylE+OudtyTUrSYcDRKI3
M95Xc/9K5Zt25GOhVUrArPn6yMXjc5N9Z7ntIg4tIc250EwtTtQFTpU7ryGM
c8ASWWaMB57UdFpKBB/A4s8zTi5QSr3Eao/HH3mAZ5F4ezK9MVt2GSlzwfrL
sTdxWIs/+JwO6tyhzEMg6zjUHEI0+mHxJ0DyaSTtHF7lTn5v3vatYkVr2Iy2
aKU3CdD7VORjJvIpB/mUN32hqQD9XAg+ipBPReCzjL7W9IWe8KWPRX6rxuj7
rXWAwreHyPfH9GHQH03Yj2as89m08L2gtA/pfIV0tYEuSvjaqUjfte95g3Z3
gN4PaN8HdOAjOn0yBqUXznynRXCklxybfggd/9+ip+n1MipToyq/RtWnhtQn
flIZn2C0jzfSwxnu4Q53U+CN9quODamOUqykRwv1xof1Rwd1R/v1RgZM/r/f
S8sly0yXmxmtt7RYbWG2ZpbxmpmGqywMVlnorzTXW26us9Rcx8Zce4kpTUNr
U/VFxidOuB+ydd9z5Nb2Qy4b9zqs2X1m1Y7jC//ebbZ2veHKZXpLF+kst9Sy
maO1aKGO9WzzFaZLNulu2a958qLKdXdOSBg3I5MlErOlJdxiBbO4nJSVs6cf
VDniEm6RnCOUsLJzmYmJeEQ4HOSv5H9H6d5tpbu3lPw9oGDvGdGBUHI4nPkA
zkkABan0MK+Mnl1CKgvgykK4tgii18iUo6+q0fZq0FGFvK0C76rQD5XY+zLs
fSn4qEA/KdCP5eiHMnpn7DsZ8k6CdIiRN0K4PQe8ysJepKHNiUhdEutDnrLv
KZ4ZB90/Fw87jGWdBTkXYNlNNPMcJHEFOReR7ItIkRsouoXVRGHF95DM84jv
dsxuIePqcvzKQuLqMuTSCsRKACed5PYVmX0rMfGzV9PGobWLzLat1fl7Nnb3
ADPiKnOpAeJ5mP+p2OyxbOfZbQZ3zzAuHjRdb8N3P4PL4sj4UOtjWxmRvoJH
pXrBfipnjvP9b6vd8dI+doAtllg/rtoQHMK55KRfkL9GKlsVFbHOx1vH1XH3
ebvlDmd5t9wFx0+TQtmxzIID6bkbH7X8P5rOOiqqLmz7cPpMDzMwQ3cMKUi3
AkqLHdgtqKAiKKgIimJgI6WUICkg3d0g3SUtDcajz/N+/3zn+H7fWtfaa8+/
HH77uu59zt73jhfh8hcvCQUEUBI/qMa/l7t+lXHoAP7qEVxbqvAshH/hMHj7
KuZxjLPTleq+m/EsSCbxldzl4/QD9pDnQfpRN+YeWzj4DMfriIKTPjchWKE5
Xj7Kh6YuCWopiKiIYGZywBVbwNcB28yBQg4wqwMomZ7IBRX4sgF41wbKvyMy
/I46GIO0PhPueUttDmEWewnV30XmC+GR90jfa3D0HdgWRKm+CdXcEq4MhHK9
ER9T6M4O3NeZHukl1VOydaTQtOuVUF8U1B8DDbwDB2PhgTiwPx4YTAQHk4Ch
v3dcjGRBY3nIRBHxlOHpGmi6HpptRGab0flWfL4dJxvTd8DzPfBcD/SNCJwD
yOIQsjCMLo5gS2MIqXFs5Su2MoOR7Xfn8NU56tocbX2evrHAIPR9ifFjiTA4
xq9l5i9iXGH8s8b8vcL+s8b+d12EsMLf37l/vnP//SH2h9Avwv74/xI8/uD9
SyC5wf+9Lv5rXeLXOv/HKv/nqsSPFaIYlPmxIvNrSfb7kuLPNe0fq9a+V1Vl
zNVVbQWq1hoq1gIlS3VCCpYCOXN1GTN12b8YShqrSRqpihuomO0+pe96VNvx
kKrdTgUbB9mtW5VsrFSsLGTNTGTMjGTNzWQtLKQtDGXMDWRNDSVNtSWNtST0
NSUM1aQNlQSmUub2/D1HeF4+EiGP+O9iOZ9yuHlE3VfCLCxlF5Sx84vp+YWk
cgvw7M+UjEw85SOaEAvHhIPhYcDrUOGIR0IxT4RinwHJb8H0KDA3HqzMhJsJ
sytGO8vQgWp0uAEebUDG6tDxWmy8Fh2rQcbJfknQZBU8WY1OViIT5eBEGTRO
MFiADH8Gh3KgwUxoIB3s/Qj0fAC64sGq11BRCPPydoqVIqolBtnK4+l+3Gwv
sOGVSG8aq+0d5XMAHHUM/uBJjT4KffJD8+4g748CT7cD4XvxNE8s+RzuKg3q
00BdJvBoJ9bwmFb0kH3CEtokgX66oz2Zp1McrrdTn64lTTFS4gYewkqe4qWJ
Us4G9CBPhS+F2inhqsedxAMvSudmnvU5o3z9ODX+ORh2j3X8kHRYCD8vQ/rB
A+bpU9CjUCj0ISswiBp8j33Jh+vnJ3nLlx96Xy083Ph+MCshnpmWdbKm0Tf4
geTZc0BCgmx8svrJE1Le3nhiNCMjTSboBjfiheTje/hdf4rvJd7Zo1T3E1hM
uGFepq73GWqoD+3jC86Fw4irBfbprUJ1mspJZ6pAEtvvJHZmr8hVV9obbxEP
Z9pZB3b+M81wbwkLJViVhUojwjo8KHgXknkGiTsCn1HBCh5T6+6hpb5Q53No
NBmtDkDqb5ONJxoDwI5QeDQJbgkB+8KAgSi4PBCpfUwZ/MgaeE+tf0FPCdWq
+mD1aB/1rQcr+zan+TnU/gxofQm3hkNtUeCXd0BnHNCXAg18goZzodEimHia
XyuRr9XwdAMy24rNtsGE2c1/QeY7kfkueK6bbPk634N868Hme9G5PvRbP/pt
APk2iCwOY4ujZHfmxXF0aQJbnqKuztLW5ugEgGvzpDYW6OuEFhkbS4zvBIBk
WzTWP2usf8imhGJ/CMR+8P8lRN6Hz/v3J3m1xW8Sw/+96ULyD6Gf/3usXoK8
J5+UzO8N2V+rcj9XFL4vS39flN6YE/xa15kc2GbpqKRkpaK6VV3FWk3ZksRQ
0VJd3lxDzkxd7v8zKGGkSqCkvH238radKtt2KNk4K9u4yNs4KGzZpmxtq2C1
Vd5ii6KVrayFuYyZiZyZkYypvpSJnqyprqyJjoyJrrSRQEJfSVxPgb9Zgacn
L6svqWEparODc+AE8/IV5sOHjPh4enoGN+czO7+QNMfCUkZxGa2sglZeQS2r
ICpBSkEBnpuNZqWC6XFAaiT0OQ6q/Yx21eFDbbSxTspEN2W8AxtrR8fbsIlW
dKIZJZtKNMAThOqQiRr0ayX8tQIeL4PGisCRfHDoMzSQBfalwz3J5Avf1vdA
41ug9iVU8RgseQAU3AGzbmAJXki8J57ni2V4QEWP6INpYin+7LpnyOcA5P5W
4L41+MQF9jeH3hzDEy5gL3ZANbc5c584CT4cRwXqXgF9qyTiroft0RESgYXU
eWDCeajzKbMxWt7VBNumLVX/Tq8qziTGX8LVmKIiTb97jlrxltKQLXHiAPvi
YZGy98yOMtlrnuwzB9lp7+TzMwUBPpKh92TvB7Feh/OvXGa/DedXlmp9TJP1
vsiIDmf532PvOSgUdEc68b1MXKzyozCNx0+ZgUGi/v5KETFmrT3Xugc8XryV
9PWjHN+P3b+DfU5lx0bJnj6CxrwQLytSunyW5eeJxb/m+l8TsTGhPL8rcctT
7OJBTrg/5fNbvs9JqpspNe25xJfPhj6HcDkWaKxOj/TgVIWINrwRdTdHRTFg
kyzDXJKhQwUPbEIPa0B7FbGmGPZwDNzzABmJgKbS4e43WP554dobQN0N4eb7
0GA02hYMDL2AY49DR1SEg/ainZ/Y8wX0ngTWULZM5QN68V3qcDp9Jg/vjSLf
CnUnoL0pyGAmech6JJ/gDpooQyYrkKkqmNB0NUwkT7KFVgPZz26+FZ1rgedb
ya5M820IqXZkvgOd7UBmOtGZL8hMOzzdDs10ILM96FwvRoA5PwB/I+LoCLww
Ci9NIMsT8OoUsjqLrk+jG1MoURV+n6NsfKN8X6D+XGSQb/3W2P+sc37/ECVc
78/fO/D//Jb497fMv7/l/v0j/+eP4n9/lP7nj9J/xOS3wr+/FP/7pfTvT0Vi
8vun4u/vCv+sy/2zrvBzWeX7ktb3pU3/55/NMRFq8kaqKgSDW1RJBi3UlSwE
iuYCgkEZM4G0qbq0qUDqL4kaLmc1Xc5ouZzQcTmm43xM08ldzX6PwGG3mv1u
1W2uKlu3K1haKliYKlgYy5rqS5vqy5joSBurSxtrSBuqSeqTGzsyhopyBgqy
hsqSBgp8fWkxXQlJXSllYzELB5EDJ9k3blHfvqGmfqSTJyw+UT/n0QsKaCWl
eGUFpbqGWl1FqSxDqkuR1jq8r40+3EEf6qQNdlKGu9DhL+hIOzrWiow1Y+PN
8EQTNlaPjdYio7XwaDUyWgmPl0NkCi0jl82xInSkAB76DPZnQj0pcHs80BQN
1LwCy5+A+SHCmQFgxnUw57pwfgBYcAv8dAlOPgW+3I8eMUbNJPA3p/C652iS
B5rqjSV5IZd1gNuWcMUTVtJFPP8SNviGHnGCet9dYTBJr/yF4g491ERJ1M1a
Z7Mkbi2F3z9MO7MdlqEIXdtJbQ5jTRRKR/uLXdqt8iZY+84Z/r1z1Gd+DDdb
7h4bPDpEJO4Z5egeBsFjzH1qWRb9zk3WqaOcpES5/Ax+VprqZS/2vRAs9JHC
4yfinzIlnj3mBN9l+3ijwYGshETbrDzDpFQ9/9u0tBSZsFB+WJhCZqbm04fc
uHfSaekKwTcpAT4U/+vSJw9g/peAN09onmeYNlb0a568O9flnG1EH95gtRVp
hYdKW2qAVw5xju8T2W1GjfCHK+Kk752nnnAWv3tGdq8ect4GI9iRowEKfDzG
V60+UiXEnbGJAmrRha1FhW5YIh2vsL4nQOcjsPsl0BeJZh1DSs9BVReF628L
98bBPWFQVyhUcRt+6oYGbgULg+CJJKTnDdL3UngsHJ6OR+ey4Z54als0bb2V
PVkIDaXDI5nQyCdkOBMezkaG8+DhPHCM7EYBfy2FJsuQqQqUoHKyCpmqxqZq
kOkaZKaWqArR6Vp0shaZqsemGgjhU03IVBM81QxPtSBTrfBUOzzTicwRRtlH
VIWEOZI3sS+Posvj6MoksjaFb8zgG7OUH/OUfxZo/ywxfi0x/llh/V5j/Fln
/fud8/eOtb9Xq5EMSvz3R+q/f6X//U+WIPG/3wSAyv/9Uf3vt+C/fzT+57fW
//ze9N+vzf/+0v39XfOfDfWfa4Lvy+rfF3V/LatN96pbk1aooWytomSp9hdA
NUUzAWmFRCIlGSQxlDRS03E5r+lyTuB8RuB8Ut3psIaju4bjfnXHfRrOBzSd
92s57NN0cBNs2666zVZpq5WStaWipb6ChbaMqUDaUFXKQFlSX0HKQEHKSF7a
SEbaUErGQFrGUEJSX1xCX5SvK8rT4cnrixjZ0A6eoAXcooe/oiR/oHzKoH3K
pGam4zmZaEkBtb6G8aWF2fOF1f+FMfCFMdjJGumgjnxBR9uQsTZsrAUfbaaM
NaGjDehoPXmB9lgt+pW8xpB4OihRLIyXQuPFyGghOpQL9WYCnclgeyzUGAFW
PwdKQ4HCe0D+baAgAMr1AzO8gbgzwMu9YPpFJO86lHABv2AC6YggW+XwVF+Z
D2eAxNPC704L3zaDA62EH9hhd7fCYU7wy72IjRT4ag+r7y1vMlXmpgMWflbw
Nde1OXHzXgumOAZocmjKfJaNulDkJcmCMMZBEzTST3IwQ7K/TOmMM+vGCW7N
J+XSLEfv4+Kn9tJiX0m+DePfuMLyucC5Gyh675YkMQ/0Bd+/EYtP2BT5Tsbz
Ev1WMPtjmvGnFLPk9zoBN1jnz/JSUhyehylnZpqVlLqmpsj5+QmdOgVe86Gd
OIpGvYLKi5Vu+XH27KLERHHzc1XPn0A9zoq9ea7mvl/s3i3R3CSCUPbpQ2j0
fcbLu2wTTfzqeemWYt1AbxlLVcTnEMXbjR59W7s7zzD5LsdABmFDACYkdGwL
p/w+cyFLITeQbcwGjUWhndLQex/mWqv8l+eMMl+o6jbY9hyv9EdLzgpXnQca
7oC9EVjXY6TjGTyViA7FYHmeUNtjZDQG6X4CT0aCI+FIykmqjwVy1hjJ8IcW
KiiLZZSBBGQwhSjeQcINB7PIJPNX8GgBPFYETRSTMJLOWAFPlv+9e62KbKM8
VU3G1IlKaKIK+lpFTiZr4IlqaIIYa5GJOnSiAZ1oRKZasJk2wiKx2U50rhuZ
64Xn+6Fvg9DCCLI4ii6NI6tf0fUpyto0ZX2OvvGN+XOB9nOR/pOoEwkql1nk
Xuga5/d3USKL/ib3Xsgs+u8vmT+/5P6QB3iV//1H9d9f6v/90v7v9+Z/fxv/
+cfyzy/zfzb0/1nf9GNZ+/uS+r8rur5eCrKmKirWqkqWpAOS+6LEaKauQJaE
JIOED0qbCLbsOm+887yu6zkN59NqTkfV7A8LHA6qEia4fRdRIapt3yWw36m2
zUXVbpv6dkdN+52CbY7qdnaCrZaqVsbKFgaKZtpyxqqyhkqyRoQVykoZSkka
iBMMSm7mSxvwJAxF+fpcng6Hr0NT2Iyb2dD3H6VevYq+fY1lpFLKClmNdaLt
LezONmYvwWAHfaCTOtiJD3egg23wUCsy1AIPNaOjTZTxRupoIzLaQGRRZKIB
myCqwkp4tAweKSF7zQ/nw4PZ5BdrHUlQy3uwPgKqIgEULggWzr0t/NkfyL4h
nH4FSDgNhO8BIvbD1Y/RxHPAu2NQ4R345WnQ1wHP8GdnXUXjjoPpPtgDe+i2
JfTICb9iIHRISXiXNGglJnzRlPLhPPp0P2QlhTzZibc/Yfd9kDq1nabEQiL9
lEujDa/t52/RoLsai23bLHrZAUu/Q8l+ztyqjXnsRHLCaLVZjvvteVdOs9Nf
82oLZB8GGR7Zw4kI5RVlSQXeZu/eSbvuzUyJoeSkcm/epD0K5SV/UHkaxn/+
RNzjIvXCRVZqkrHXJanEpF2FxTsLSva9fKGWkmZ04w7X5wb7zm3KDR889AHX
24sdcpOWHMO6cZXpcYb7OUkq/Imo5yH8gT/18C7YUIN67bzYQz/2Llvq1SO0
8lil94+5OnKQk7X4m5vc0OPieY/EI67TLBQQd3vJfWZcLVHY0wpOucE+bYTr
i8FPjkoX3ROreEVdrJGJPkVL8cDrbiGVvuCXl1j7S6j1Edb1Cqm6Dtb5AZ1P
ge5XcO9ruDkI6n4O9D4GBx+DzcHIDXPYThKwkBQ+YgIn+aCDCXBfLNAVDXbH
gr0fwL4UuC8d6f+EDOUgw7nIMMkgPFZMLLDwRDl53+/XKmiymtQU6YCkCZKq
gyfrkckmhBin6tHJevRrA4EeOt2OTn9BZ7uwuZ6/peIgujCALg7hC2RfEmRl
DF0dR1cnMFJfKSuEiLJxmko44/c52vdv9B8EiX9hJEj8tcr+tSrya437a533
e0Ps93f+7w3xf8g9GWKU+r0h9+e7Ivmx6A/13z90/vzS//en5b8/rP/ZMPyx
Ivg/P80jnirLGqmobFFTtiLrQQXy9QRREqoTGMqZ/Q2lf61wx879rjsOOrge
2eJ2ytjlvJbrKTWXI2qOewX2u9W27RJsJ0pFB0UbG2UbW1Xb7Upb7ZSst6ps
sVK2Nlfdaqlmu0XVxkqw1VxgZahmpa9qqStvoixtKC31l0GCRHE9UYnNHAld
loQul7eJzRJQ5XSYFzy4WWnc6mpWcyOzvYUwQXpnC6OnldLbhve3oQNtaH87
OQ6240Ot2HALPtxEGW0khJFWWPf3m+0qZLACHiwnhAyUIQPFyEAh2psHd+WA
HVnwl0yoJQVu+gA3JiD1sUh1FFz6Gsx9BCX7Aa+PwJEnoLzb8PNdws93oYkX
oOqHeOtzvMhfKO4IWPqQPlfLS73BjthD7YmR/eBFPb4J3CEp7CwuZMETshIX
MuYDGmzgnAkctp/y+hxNXVzYToAUBDBHU/l1ifK6kpj5JtGKOKO0tzp3jjHP
uEkecBY/v0/c6wAn8BL92inx+/4GsZHHgy5TkiNVwl/LXj9HuXtTLPQuJztF
JjpKztOTftMH9fJgvXwp8vQZJeguO+sjPy5W5tJlemWlvZ8fP/KdaHS0dHTM
luJK+8I8/avXqUnJvA9JEufO43FvqLnpvLt+0m9fmMS8NT+yH7vugV31wEw1
Md/LYkG+4lu30Py9aU2f1Z/c5KlLwhf2Ai6WoLuLWEGUTl289iFzdJsiYqoE
e+8UqX+m2Pxe4YojzhMCFCiAIg542DI/XaTV3Ka8P4TFnKIEu4DNL5kD4Xjr
A6SNCJ+RyNAHcDQB7niItzwEO56DrSFA7U2h5ntAXzjYfh/seSRcfwf6cIaW
64PVPKC0v6B2PEW6w8FOQhFA1zugOxHsSYK6U8hbgPoy4f5P0GAOSKSa4QJo
rISo9+GxCmSMCDyV8EQV8v+FfiVIrEcm6mHC8r42wOSkARknf8KTrcgkgWEX
OtOHzg3C30aRpTEiiGLLU/jKNL5GBNE5fH2OuvGNZI2oB38sM34sM38us0gR
0JENsrmE95G7MT+Jkf/7h/jv7xJ/fkr/Ia9Wk/3zU+HPT+XfPxR//1D4/VPp
9w8VAsM/35VJHjcEfzY2/7tu9XPV5M+aakPhZi0zWWVrgYqVupKlBrkt89cH
5UwFcqZq8qbqciYaMibqLk7b3BwddzntcHXZ4+h8xNr1uJHLYR3ng+rOB9Qc
96g67VZzcFKzdxQ4uArsnZTstijZWClvsVC2NlOyNlfaYq5oZa5sZalsaapk
bqRiYaRqqadsqa5sqaJiqaZgKi9tICFpwJPSE+HrstgaLFNb2suX3PIqybJa
XlUtu6mO2drIaG+hdLRinS04iWEL1k+Q2E4daKMMtOIDzfhAIz7QgA3WI4P1
MKGhOni4njxJQe6XNsJjjfBoEzJGWGQ9MlyDDFUiJJUlyEA+3JcD9WaDXZlg
WxLYGAtUvAJy7gEJV4VjL4Dxp+Goo8Lh+6DwQ9BzN4T4WfsCS/IAP3pTqp+L
hJ/mlN7Ch8J5PXGskGPoHhU8wsP43BaOCR80YMObRUA9PizHENrEFZbGhfUk
oaBdrHR/7kVHXBQTurST0xbD+Voo+9KPe9JFtj5JeqBa4bGvlNchkaI4bmO+
8oOb4kE+rIx3pl+qtMNCRE8dEXkWSM//wEpNlHjyVDQ9Q/LRE/EAf+6b1/Jh
T9lF2dyoF1yvK3h1g8HrCNWr1/Bbt5iZOSZvw8WCgpj79yEP7qAlebJXL9GP
uUPeXpiPh1hVnl5DhcEtH0mfSyIf3sufOsy+4Y2Vpqh7HKHttULDfLGX90S3
G+NnDkh6ukses+dkhDAro/hnHCiy4pQjTjLednCSBy0/kHrbGVFlA1IwIEEV
MpUA7m0HQi2hZ3vg0hCo6Rnc8gQuvATV3MZrbyNVN4HSK3BfBNzyAGsNgbvD
4L6nWO55OOkU1p/IGXqPdj8gL8Nf/gR9S0P6XhC1JNz2FGx/RkRZsD0cao0A
2t9BXfFQdxLU8xHsTSUYRPqz4MEcZPAzUSGSnjhUDA2XgCOl4Gg5NFIBjVXC
pKrg0Wp4tAYZrUFHa+GRGni4mhAyWkvULOS/BFG/TLRRJruxqR4SxtkBZH4Y
WRhHF79iy5P40jRleZqyNkdZ/0Zb+0bbWGRsLLO+LzG/r7B/rIr8WOV8XxP5
sUF2yv71XfznOqkf36V//pD9+UPu1w+lXz/U/vmp9uunyq+fgl8/tf/5of37
+6Y/P3T//NQm9PuH3s8N819LJquTmvsOKsmbC1StBMpWfxm0IIKohryZQMZU
jYij8qYassYCWwc7O0c7J4dtO7bb7dy2bZedm6ujO0GioetxHdcjmi4HNZz3
aDjt1XTeo+7krGpvp7rdVs3O5n+lus1K1dZKcYu5nJWJvLmBvJmugqmugpmW
spWmkqWWopmqsrmykjkZU9VNpU6dl0xO5RdX8koqOVU1IjWNnKZmRkszo62Z
0d7M6CDcsJXeQ6iZ1tOM9zZjvY1oXz3SU0uM6EATOtiCDLdjo+3kTim5UdOK
TLSiY03IX3MkngU0UkU+oOESiOwBWggP5oEDn+G+LLjrI9QaD9SEAyWhQNYt
4cwbQMpl4ehjYNR+uDgIjjwEvz+B9H6kVDxm3rCDnTVQQy4c4U6r9IOKQpGj
6pC3BW0622gkW/v5BXEzPhh8TCc71DTMS9lalSFDBYPPmVW8NUkOVjdSotNQ
oUPG9PhrIsVhrJ2myEFz7OMtuDWNFXBe3N6QFeoFZr6GvE6IH3Lm+59H3z5g
P/RnJUWLP7zN8b2KnNwPJ8WQX24/fkDLzOCnxLMeh9BSPig8eiB51ZcVESX9
8rWEbwDz/Dlqaang0yeVm+ROl6KHJ+1WAO38KeaRo8ywELF3r9UCr9FePqL7
eVO8TtMSX7KC/JgHnanXTiOXTyDGWtSTB1iHnRgHt1ML3irUpWo76sDOpsjN
E/Tt2uwXPmKdqZr33UXczThe21gCprA8Ez5oyQg6xDYVg615kIs4/P4crSMS
G08QGYmkDMQgw4lI+0Mk97hwuRfSEoJUXicvwG96AIcfxg5rAB5WSNsHkcUy
1nAkOBEDz2ZB8znoZAY2mAB2R0BNT4DaUOGax0DtM6D+JdhMOGYM2EmQmAz3
psGEGw7kgMQTJKxwtBgeLSfKPXS8Ch2vRsZroK9kw2V0/H9354ixhnj68FAV
MlAB95VB/aVwfxk8UAkP1SAj9fBYMzLWQm4sTLShX9uRyS5kug+eHUTmR/Bv
Y/jSOL40QVmepC5P01bJVxjMtW/M9UXWxhKbRHKFvb4qurHG//FXG6v876sS
31clf6zKrK9Kra/KbKzKf19X/v5dbWNDc31j09r65vV10431rd9/2P3YsNpY
dvi1sMn7opKsqUDNSl3FUkOZsEJzdUUzjb/1oEDaRI0AUNZIzWz7VuvtW+23
2zrZ2rhssdhhYeJmaeW61cF52047Z3dzF3e9HYc1XPYJnN00XHYInFw0HO01
HLapEbK3VXe0U3fYomJrrGRtpGRlpGShp2iurWyhp2JpoGS+Sd5UIGOmLKuv
Zr9XPixcJrtAvLCYW1LBraoRq6vn1jWyCTU0sVqaWe0thGjtTbT2RnZ7A6Wj
Ee1swLsb8J5GrL+FMthGHf5CCBtuQ0db0fFWbKwZI8/UE7mU+DvXoGO12Gg1
MlIBEwyOEEUi8dQKYaK67/sEdaWA7fFofTRc8QgqCAJzAqC8W2DxPSDjmlDy
aeH0S3DcSSThGFL2CHm9H/E1E3ZWA3XEha/YMSPdsaiT6HkdojaE2x6LdcRo
XnXAN3HBNye4kymC5YrtYZeljCWwpGviQ/GSvWmqu4wZTgbShc8EJVG6Ieck
DdUZXgcMQzyVr+6jPA+0e/PA7Hkg/+h2ZsTTLTmxauEhUtfPM5/fppQks3NT
NO/7c149lnx4R+buXYnrV2iPHzDv3sJC7kreuSGe+VHmU5bEqZPIi8f04hJF
L2/2LX/O/TuMwAC0vFg3M2tnoB/944dNV6/Iv7iHJUbzPU/gocGcq57cs4cZ
wX6Ms0dFDrpwnoXInj3MPbGTWZgi+BipcXQbLfgMGn+fdn4PpsFn7t3GP2lP
e36G0hIrmRPCM5IDZGkQC4B2GTNLQ0RGk1RjL1EMmKAZB9glDQSYAS2PqL3P
0IZ72GgS2vsMrvADe6LQOn+k0gtqCYI/nUXO6CCHtZHQ/VDpPaQiGK25g8xm
49/ykMkEoaU8eLUCW6/GZwqg/jS4MxFpjUbqXoM1r8DaV2R71pZYuDUBbE+C
OlIh8s7Yz+QJtdFSZILsq4URFd9UIzrZhJFqRr82IxNNEKHxFmj877JM4Dba
jI61oKMtxEKNTrSjkx3oVBdCqgeZ6kamewgGsZkBbG4I+zaMLYziiwSGk7Sl
KcbKLGNljrE2z1hbYK0viawviqwtcjeWuevL3O+rvB8kgOLf1yS/r0t/X5fZ
2JDeIMZ1ufU1xfUN5bV1wdq6xsqq3vKy7uLipm9LVvMLzt8WnH6vOFz1FsiZ
aKpZa6pZaalYaCibayhZaCmaa8iZqpMA/r3pV8/G3MTWYoutpZ21hb2lmZOZ
gYuxrquR7i5zs912jjscdm9zPmLodEDDZZeWi5uWi5PAcZs6ISd7gdM2dYdt
AnsrFVsjla2GylsMFKw2KVvpK1sZq1qbqllvlrcgeDfYf0Yp4aNEbrFYfqFo
ablEeRWzsoZdVSdaUydW38BpbuK2NLGa6+nNDYyWBnpLvUhzHbW9kdbZwupq
ZXW30vtaaP0t+GALOkSoGR1qQIbqyfWNPM9LbpOS9BH1wmg5QqA3XAiR+zM5
5IvC3gyo8yPUngjVR8I1L+H6CHrUVdq1bcj9PWDCRST3Niv1Ehp/DPzoCcef
Ap67Cj/bCX64jH70Rv0dKVGXuM92I3cs4bvbsAtq4L3tNN9tPGsJohgE7znB
9cGU+jDJA6aIuih8yxX67EtLviWnI8UKOirR8VZ8skjrohvVe7/aQLZhV8mm
3eaiwSdEej6Jln6UcttCf3aVVp3MyUqQPuxIO7ObHnSZGvtCISmSWpbJTIhS
fReuWpSnGHKf+/AhOytV7PJlOD6K9voxyz+AEXCNFhfNe/pULiVT4/o1yp6d
UJAvK+S2qOdRuDCb9/Ih//Qh2tE96LULrMZKnY8x+tc9qeVZcs9DpY7vx4uT
5N6Giu8wQV8HUGIeit08KXJ+N+/6WVFdOfyOp2Rz6qbcl/KHDFCfXXRXLZqb
OTvan3djp6SLMjXHl9H+mv76KLaZI6wrImzLFg5zF+l4L9IQgmQdheuC4KYH
YHc4o/st3HIPrbsO1PuDLffhigA80R394A51vMZzLoOpJ4D2cHC2mD2RrTyX
R1spFlqtgn60wust8EI92eRlKB/qzYI7M9AvKUjLB7gpAWxMABvi4cYPcFsK
2JEGdWcjvfloXxE0VAaRVliPTjQhU3/3PKcJytrw8TZsrBUbJQGEybEVHm2F
xtqRiW50ogch+1f2w9P9CDHODCAzQ2Qf5/kx7NsEtjCBLU7iyzO05Vn6yjf6
6gJtfYlOxtE1gjvOxqrojzWx7+tiG2sSG6viG6tSZP/rNan1dZn1ddmNDZm1
NZnVFfm1VYXVVaWVVeXlVZ3l1U1LK9qLi4bT32wnprZtLLsF3dWXN9UUWOsQ
DKpZaapYaBIMKhAMmqjLGZMYyhiqam410bU2MbU2tbIy2WJhbGem52ii42Cs
62xm7Ga1ZYetk6vDLnunfZYuhwycduu67NQg6HPcpkEA6Lxdg4DR3lqw3UJt
u5manaGKraGajZmyjZmKjZGSpa66hfpFH/mP6bzsPH5eEb+wXKS4QqysSqqi
il9ZI1rTKFpXz6mtYdfVsOprWXU1jIZaenO9SHszq6OV3dnK6WxldLdQepqw
vka0vwHpr4cH6qGhBmyYUC1KJP/BSnJbZqAEHCgEyTP1n+HeLKgnA+5KQ9qS
yUdZHwPURAiXPgWb4/HlToWXN+SlqbAyB9FmQ347pIpCJNIuwnHHgYTTYPRh
uPQpVvMGyr4PZnjDSeeAe7bCr/fhBaGiPtbYPkUhGw7gygXseNA+DfiYDnTW
mqbNEyaqQiNxITd1ZKc+zseFjpsAKTcY+U+kzeWQiw5o9Qu0JJprb4jfOcdK
CwSe+8BbDBhnd3CCznNDfVjvn3DqP0u8vs/ZaUkP9Ja/44M8DOCkxjDzk+mh
99C4KFrqe7rXZfw86Wv0vM9SwbfpJw+KRb00r681f/FCJuSB5Msw+pEDFPeD
FL/rLO8LeGI0LzRIzMUOeXiLHhYqcfGEeOQdPPEVZ6ct9fIh4cArFENN6Lgb
86wL7fIhvCxBUPtJ10GL4nOIVf6G0/JBycsFk2BC4jQs5gK3NUK6IULKTQDs
1kb87VE9KrKJBZ20ZoQdpleGcadLlCKP0TMug2XXoaZ7cMVVsPAM0HAbHCYs
LBQfSUYbgtB3zmjWKXA5E6+6ASfsBVufwAPJlIFSy5kvB79WmI9+os4VIws1
Qiv1+GorZbEZna6BRsugkVJC8Egprb8E6ylAegrgLzlAWwbUng59yYS+ZEEd
OVBnLtSVD3UXwb2l0GAVNFgDD9aig7XwELEsN8LDTfBoM0Ji2IaMdaBj3QSA
6CSB3jA2O4LPDCMzw/DsKDo3is2No/MT6MIk/u0rZXGaujRHW/7GXF0UWV1k
rS2zN9Y4G2tiG+v87xsEcVJr69Jrq9I/1mV+bBAOKLu+Ib++Lr9OTEgflFtf
lV1blVtdU15Z1Vhe0SBJXNKfWbCamN6++M3xRdhmeWMNgfUmNUKW6moWWspm
moqm6gokg6QPShuqqlgZaloYbrYwMLYwMjXTtzTVszHeZGuiu91U39nC2NnK
0t7G0sFmm6P9fhvnI0auh3VcXNWdt2k6bRc42ak72grsLQUOW9Tt7dS3W2ps
M1O3MydglNtiqG2rdiNQ6kMmLzOb97lQNLeEl18uWVjJK60Sq6gRragWq6ji
VVSJVFWLVFayqqqYdXUiDY2c5kZOazOztYlOWmEj3t2IdNXD3XVwXx06QFSF
dUh/NdxfBRHJf7AC7S9H+0qQXuJxEM/rM7GQwq3JYFMiUB8L1LwDqqOBqiiw
IhwoegY3xONtCbTY6yI7DeB9hsiJzfDbI9QiX+zjKTB8D/RmP3jXEXtxkpIT
gH8OQLKvo+ne8Ou9aOlTkYUaqd4UjY83JffrwVvZwgHO8kUvrYOPKFpLgcZS
LAsFrioXFUOFpXFAW07UXofrqkl1MaIq8Sguutit/VTfgwx9ScZhR5bfYfYO
c+7tC9p57zXjXmhdP60QdUu6IhGPe8aJfiZWkbf73i1nzzO0ezeoj+8yblzh
+PnQLl+gxcVp3bkjHhrMLP7EevyAERAoevks5XUYO8BX/lkIpbZY/n24Qnwk
7WEwY5cblhrPjotWOHeSdt+fdXIv4/IZ2Zte9JN78UOu3IdB+nevqlw4qJYc
oRMeqrrPjp0RRGtMUbiwnyJHg6/vpYacYR22EQ8+r7rPUnSHLvLxMv3decoh
fVCZDcrgkAwivH8zknqZUXWX8ckLjDpBubAZTvZl9UdSmkLgtodYzmmg+RE6
EIMXnBGe/ETtj0MTdiOFnsiXB0jxRbDYC2y7C9cHIm9O01tzdeZ6dhQ8km6P
E/tWwprJQ2dLoKVaZKUZW2pB5xrIjw9Hy9ABsn0kPEoUgHXoWANOZJ6hWmSg
Fu2tQrrKkM4iqLMQ7iyEukqgzmK4g1AJ3EkK6SyFu8qR7kqkpxruIxbtRmSw
GR1uQ4a/IGOEJ/ahX/vRqSFsZhSfHcPmJrBvk5SFKdrCJG1x5i+G84yVRUKs
lSWR1WWx1RWxtRX+ygp/eVVsldCK+Oqq5MoKIamVFZnlFYnlFanVZQJPqZUl
2ZUlhZUl5aUltcVlzYUF3bkFw6+zNvPz9tGR+vImAlUrbVVLbYGFhpqZhoqp
hrKJujyhv8WgjJGqnLmBipmupqnOJtPNBiabjI11zY10rYx1t5ga2JIp1dTG
2myrtaWdrb2j/d7tLofMduzZtMNNa8cOzR1Oms7b1Z3sNJxtNBxtNRws1beb
KG8zV7LZbLdPJ+SJVMonsbRc8U8FokQQzSuVyC/lF1fwSso5JeXc0nJeaRmv
tJxZWiZSVi5WWc2tqRUhMKyvYTTWUJtqsOYauL0O6ajDOmuRziqY+JMSf39C
/ZVE6Y30VyC9pWh3AdyVR6yKSFce3JkNf8mA29PA1o9wUyLYEAs0vIdqo6HK
N8JV4VDlayj3IZgXiowViYwUSYafpqVfhPOuw5keQPFtKMgB9HOihB7EvXWE
rm2CXu5Cm97iDeFo5Dk0M4idflWsL44RdhI3ZQJvjojPpMiP5ph62nHeeO3u
yXApjTQ44sA3kGZmPbXtSjfMfqqgL489vqBVHqlV/E7vkA3/wXnphiTNgjh1
Wx3Gm5uspjhGWaL4UUcpz4MyN07Rgr2pqS+Rko8Kz++o5sVyyz+J3w3gZMQq
xLwRvePPrKs2jXmj6X2e7n8V8zjBzEsViX/Hv+2rFewv4XkKfR1Kf3hTIila
6vFdisd5ZtAtxil36rMgbkuFQsAlkeAr1JpslaBrYjfOilWlaL65I3dgO+dd
EDvrpehBO2SnGeZ1gOlqgLg7ijy4rnzORTzqunRHolZNpLiVImQoiaoxQUUm
aK9DCTzMu2jJsJWGHjlDSUfhyntwqgf8chdedJ3eHIg23IeG3iENj+CWx3j7
AyTTHWwIwqez8LKrQEMwnHcOzD0B5F1C3h3ArpqBfg74SCpjpVm06InE1xq7
mQbj0XThsUx4JB0az4EmC6G5amSxEV1qweab0K+18GgFNFyODJai/SUwuerW
wEONyEgred0luS/XgY90YMMd2GA7OtCM9TVhPQ1IZx3UVQN11iAd1SgxdldD
PXVIbyPSR+SoRmygCSEqmuE2eLgdGvkCj3bCIx3IWCc21oWPE+qmTPQwxnto
E320qQHW9CCb0NQwe3KENTXKnh7nTU9ITH+VmJmUnpmUmp0iJD5LzuVmpmVn
Z+TnSCnOTqvNzarPzuhNTRuMT5l/m7d/8cJYwWCTuvkmNQsNVXMdZVMNBVMB
QaWckUDGQPXvYV5lGRM9eWMtJUN1dQOtTYbaeoZa+gZahkY6Jqb65ubGFhYm
llbmpLZYWm21tLW1sXM6YOF2XHf3Qb09h3R27tZ0ddZxcdBwtFJzMFazN1Pc
Yu1yWO15pEhKBjfzs1hmAf9TofjnIl5esVhhKa+oVLSkTLSkVLS4hFNSyi2v
5JVX8MsrxSur+NXlzNoKWn0V2liNtNbgbdV4awXSXgF3VBJCOiqQ7gqkpwLt
IdArQroLIQLA3kJSPYQPFkPEpDMXbs0AG5LA+jigNhqsiYaqo6G6WDTxDv3G
Idq13XDAbrjoIb3wsaSLLn2rLPbMnZp/HS+4LpR8Dkq7hGT4QP7GgJ+JcIAx
kOyBtkXioYdRK2nyW5oyIkmewKxFgZAd7Log+pMDNBMRysfL/MkMlZFsnVMO
TAsFKN+fM56kkBFMN5NB4rxZg4liXWmm+82YEZ5QXyy1IIKvqwC5mcB3z7Ce
XqNnvBLrLFGPfCB33JXuf4p57TSVyIrJz9HYMCTQi5YWRX0Rgvteob99IQjw
EX0cLPb2tSDgxqb3L5l3fBivwvjVeWI3r1BOHcTDHrBePhE5d5SRECH1OVXq
yD7qPR/ZzHfS184xjzqBEffpIX40Z2PgznmhZzfZm5Wgg/bolX3o0W1Uv0sW
106Z7LZCyl6LDxbohJ5kXbEFS5+wSh6xDprhSmJCgBCoIYq8OUWrCeFUPhQ5
ogW6yYE3TeG3x7H4U0iaB14bjLQ+RWtuQ+2PkabHtI4X2EA4WO6F1N2Eu57A
ld7wl6doyQ1s6AOe6MHcygDMRcATm8H8u0hjNHZ5K5IcLDlRzPv6ERtIBAc+
IP1JUH8yOJAKjmRBEwXgbCW80IgvtCLzbdB0MzpRh4xUwQPlcE8J3F2CdJXA
XWVwbzXaV4v0N8DkhnnrX6w6kZEeZKwPGe3DRwfw0X50tBcb6cWG+4gRHenB
R3owQsPd+HAXZaSLOtJNH+2hjPUSE3yshzpOzunj/Yyvg/TJQSZB3/QIZ3pc
ZHqCPf2VOzspOTclSXA3Ny05Ny31bUZmYU5qYU568ZvC4qLS0pLS8ori6qr8
yrLa8rLO0pLJzLzV1KTp8oLR02cGUgaqahaqyqY6ymYaisYCeSO1vx2X1IhK
UMZAmWTQaJOMobqcvqqKrkCwWaCur66hL9A21NQ10d1sZqBvZmRgaWJkZWZk
RYwmFlvMCUPc5rTPfM9JvX2ndfce0t65Q5ssDC2JUKpqY+h8RPHNW/EPqfyU
HLGsAl5GgXh6rtjnQvG8Yl5+qXhBKb+gWLSwWKSkjFtaSdAnUVYuWl7Orqhg
1ZTR6iqoDdWU5lq8pRJrqaC2VFKby+HWCri9DOkoRb8UQl8Kwc5CsLsI6i0h
gijSTxSDRBwtJZAE23OA5nSoLhGqfAeURwhXRAtXvwfqE7HhYulnF8X4ECCO
ASo02EGT6ijAjGUBRQagKwZdsGSlXlFIOYsmHAQ+eGAvdkOh9lCwDXjXCow+
BL32RLZKAzedWI/s0RfHKfsVgT2KQqd1MWd5SB0TumkLNTySSLshpy8hrC4q
dNsRT78tesUFlqEDV+yhDD807b7SVm3eKSv01QVq3GP9297mYTdVbpxRO2GP
fX6OdX0S+fhUMegiszpnc8wrmz121JueLI8jVI9DjDehsl4Xpc4eob16JHbV
k/kxil2coeR1TurCEephN2rMa3puItvjOHbXl1qayXsazHO0ob9/w3n/nH79
LP1jhMyjAFH3HTyPI6JXTrEuuHNP75PxO8856sLYu4Xrc0bGwZjx8KpoV55u
XpSejTIU7oF3xvFvu9OVqYCnPWqrhFip0oOPy7uZy4pDwl7WUJEfVhyAH9KC
DRjCTiwhV55w1Amo9jY2m452RaGd0ayCC0DmfrD6JtgcBFf5gZU+QIU3mHmW
8nI/5eluaCiL2p1Aue8Ah7ihYQfxrCB67BVkux54YAsUfwv/mk/9mg11xwt3
JQC9H+DeRLg3Aer9ABEwDmaBo/lkq/qZGmi+Ef7WjM614NMt6Hgz+YK4vwbu
r0Z7y5Gu0v8NosQEISYdRFKtIkwQ6a5H+prhoXZksB0Z6kJGCAwHsLEhfHwE
mxzFp8cpMxOkZifpc1OMbzPMuSna/DQ5n51mzs8yv82yFudFFuZFFufYi/Ps
hTnW/Cxrnph8E1n4xllc4CwvcVdX+etr4hsbkhvrpNaJcUNibU1uZVV+eVVz
aclubsF2eck5Md5USVdJzkxNwUxAXrJtpCZvqCpnoCZrQACoIk0wqK8oaaAh
oa8ipacop6OspKWspKOqpKuqYiAQGGppGOtqmehpmRlqWRhvsjTRtTQ2sDQ2
tzC22Wpru8PdZM+pzXsPa7q5qjttEThYqNqa2burP4uS+fCJn57D/5QvkZYn
mkpYYT4/p1A8t4hPuGEOURgW8wvLJAvL+cXlYqVlYiUlrPJyRkU5vaacVlfJ
rCdUQakvR5rKseZyvLkMbSqB2krhtiKwswQifLCvEu0nlsRKpK+cIBHqzAfb
s8HWdLghGamKByvjgKo4sCYBqk+Ea96BVZFASxLj8VGWsThioQjt1IEvWMBh
+9BXe/EzZoizFuSmQ4311cgPZCWdAJPPwO9Pg89dkIf2QKAV9MwVjr0IvTiG
vvfAr+iCUSfx6NMUDzOKnRRkwoP36fJPmPAv2Ijs0KUJuIi+HMtIFjOUQTfx
MTMV5sktIse3cPca8u6d1S2MtEm8p3vBTbUkXH4iX7wolu9iiF3dy4gI5pxz
E3l7A+/Ml8yOkwm7yW34LBf9iu91kp6XovsgUC3iCa21WC7svtiDADzQm+Z1
jpb8TjTuLe/mZcr9W6LXLkl4HWckRTIDrrEf3Ze860s7eQQ5uw+v/ayWk2Bw
5Sy/JFUpP1XnpBsr6ZnEl0LriwelQ69xWnM0fI/JXtjGLAujl0Sw3QxAW3XY
Zzdip42Za9N0pRmqPGqCn2TvR4WmCDlrFVSRAtxwo+9TRc1Ewd1a2B5JZLcU
nOUHdT9EKgKQD1eRyVKx8mtolrtwkRdY7AmWXAKqb0Bx7vAeacCCD16wgsvv
433RyK1dsNduyhVXxN0a8j1JdTIF7cyEt+gj3nuR8ihsIhcbzgC64oGuWLg7
DuxOAHsSoJ5kqDcZ7kuB+9OggU/gYA40XAiNV0CT1dhUPT7diE22oF/byJcR
w0TR1wgPNCB/3ybDf5sjwET90lmNdNTAnbVwdx3UUw8TibS/GRpsI/InNtpF
bteM98DjffDEADI5hE0NozOj2OwYZXoMnx2nzBLjBHWOgHSCOj/NmJ9hLMyz
lxa5y0tiy4u81RXe6hp/bU18bU2CnC+LrSzzyGqRFFEtSi+vyC0vacwvb55b
tJr5Zhf7zlygrylvqqpqrK5oTDIoa6BGYChNcKevRIinr8LTU+LryPO15fga
8nxNBQltJRk9gbyBlqKxjpLpJkVTfUUzE2VzE4GZIdnM3sLE3Npq67bt21x2
Wuzer+PmKnDcpmS7xe2kzqsofvIn0fQ8yfQ88dTPomm5/Ixc8cx8CQLDzDyx
rHyx7AICQ15uEZlLS4lQWsYqK6dXVtBrqxg15QR9rIYqWmM13lyDt1QgTaVQ
WwXWUYV1EctaNdxfhw7UYv1VSHc51EkgWQAR4bM9C2pOB1sywLYssC0HbslC
m1OhxkSwJkq47DlQ8ADKug0mXgbfe0KxnkDieSDuBPDUWejGZuCVG5h/Ay6+
Qcm9CiSdBiN2Awkn4Q+eEAFg8FYgO4DakYTm34cjDgAPtggHbsEKAqhjCYzx
FPWg/VR3bUbLC42JXOv4OwJdLnTPXa8zdWdVlL6dLp2HAVFeslO5qjVxmocs
RfOC+JPp7LYEpWO2jMD9Qsm3uB+fG+yx4UYESZbGy3vtZ17eT/E9jNw5x4gJ
oeVFQU/98IggdmEiM+Q6780DNDqMCJ9id3xEYt5q3PVjfIqj56SwPY+L3fam
NZTqx7zW3O+In9yJ5iVwE8NVr180vX5O4pY3L8Rf/MB27JUvmvycdcgOv3+Z
VhDHvbyX4+NOTX3IDb8jaigrfHg746QT46SbuJuJKA2CPHdwiiOUqqMFR4zp
IXsYtY9puX6sA4YQDxVWgCBLSdrTw/S2l5zMK0wPVTjjMlZ0DbykCx3QguJO
wmkHhNPdgUp/rPQCUHUZargFhu1CzhmiobuQp65IsT86/hGquI/mBaE39gE7
tgLbzAFHK8DBWpiQlTHgZA74n0Sq31LGs7GBDKAzAfgSh3TEQd0Ehh+gvo9g
fyqBIdybAnd/BHtSwZ4U8p1vdzrYkw315cP9xfBQBTxcC400kF9MjTaj4+3Y
+BdsvAMb70THCBG49fw/jfeikwPY9DA6O4pNjyAz4+jsBDb3FZ/7is1P4XOz
1PlZ6rdZ2uIMfXGavjTLXJhlLM4ylubIcfEba+kbm7TFOfYS4YOLnBXCCpdE
V1fE/oq3tsJfW5FcW5FaWZJaWZZaWJCfm9OYmdEhCsPZKZMDBxTldNUUDTUU
SBNUJU1QX5XsfWagJLVZWUxflbtJUVRTTkRdiqEuxdKQEdFU4OmqihtoSBrp
SJnqSZluljQzkjYzUTAzVjcz0bE032xlamZtamNjs9XJzdR1p6aDo6O79pO3
oompYoQDEuEzJUss9bN4+md++meJtBxe2mdxksc8fkY+L6dAtKCIW1gkWlTE
Ki7llJVzK8vYdZUMIoU2VtMaquhNNfTWauxLDdZeg7fXoN3Eykaub0hvNdxd
DnSVQoQhdhTCHYVQZx7YXUhU6yiRSPtL0O5cqD0NaE0Cm9+DNS+BslCg6B6Q
HyicGyicHwh9viWcdgV46gRdMhC+qAO/2gPEHEZijguneaFJZ5HYo8KJZ6HE
i9BNE/CRM6XqJb01llr0mJJ0FY46hL4+CD+1x+sCGANvWSf1YHdtWt0teCJF
/pk7U4Um9PoobSxOviNW2UZFWE2MEuPJGY5Tzn8su0kUubkD+3yHnvJQdpM8
tsuI9SrAOuiMkZcrtTZBZLhU7OFNzhEHiejQzV6H2Yfs6DFhdpcPc0MD6Pd9
RY64MK4c5ty5KR1wlZMdQ28uVH3ox/XzwHxO01Pi3e/5yMQ+QZ4Hsx+FyPmc
ZwddhW9fpT725VflqPtd5J0/bBAX5R3gIetuQ7HSRQ/Y0/3PMQ7bMg9YcT13
4vttWK7WLGMF9iNP5YFc8/Y0bRNF6jV7rPklpzte3M8NMZOBL9lQLcUBFVFg
kyykigvZykBvj2C1AbSim5RgC+z9YfiZI7hPGXKSh8J3wkk7gPKr2FgipfQ6
UHQRrveFK66D47G0jidY8lGo/i5lKgNui0QqXoq/91ONC+SF+6Hex9BdDpir
I+BgB9jagCbmoAOx0J1GS8PxzhSsOwXsSoLb4+GORLjjA9idAvdlQn8/YEP6
s6H+HLAnB+wmEmwW1PUJ7MiA2tKR9gy4PRP6kgN15JL7pd0lcG8FQizXgzXQ
QB082IyOtJMfeBDRdOgLOtpJOCAy3otM9GNfB9CpQXRyCJkaIt1wegibHcZn
RwhDROcnCDZxYpyfoBCG+G2K9m2aPk9E1inawgxjcY5kc2mOuThPpta/4izO
iy194y8tSCwtSi4sKMzNqs9MaU1NGy/Nbvc+LyutoaloIFDUV5XVV5XZrCyj
r0Jqs7L0ZmVRPTW2tgJbXZalKslQEWeqSTHVFTjaKmKbBTxDbZ6xHt9sM99M
X9zUWMbMSNHCWMXKTMPKVM/K0MDSyMzK1MTKzG6XftBzmbiP3I+fpJKyxVJy
JFNzxNM+8wkSP37ipmTxU3MkiJ8ZubzsAn5+Mb+giFdYLF5MWqFYeRmvppJb
V0Wrr8Rqy/D6ClpTDa21hkwRXXVYdwOltxHtqSOjRXcl4YAwkf87S+Cecqiv
ChmuQ0dqkWEimpZB/QVQfybcnQy2xQIN4WDNc6A6DKh8AlQ9BWqfA1VhYOlD
4MMF4QBrwNtU2NcciDsHhu+FHtgAKReR6mdY6mXwmRMYYid8ywJ+fQh76IDc
NMS9tKE7dnh7AjvDD/cQCEXuQaMO0ax48FYpIPYYs+oe57AhpIBBN21hYh7v
K6EhBUpTgYP66NvzUme2U/g0aJcB59UFufgAZRttWkaI4mS5YeE7xTP2lDdX
4dQH+I0TzNTH8mN1qtEPpC/vFWkpNHpzX/ruJaOitK0v76u8DmLX5fAjn4rE
vsCiQmXvBzsd3CGSGC5Vlqly/az4sT3I7XPU6hyljHi1vc6MLYa0Ox5IcaLY
xf2MYC9uV7lL5nvnu9eMI+4p5MVrHnGQCbuu8vG15s1zYoHnZetTtGODlcKO
UfoT5cbyVY5bIMYy8MdLWMJVymlLQJ4upM7DzOTx6zvEsgOlrjmydFHI1xKN
dAHe7IA+XgLfuEIPLYUfOMGv9wNtz5GiC3CGO9QQSGm8izY/AOtvoQk74ZEE
rPcl1hSMjUZCudew6HOsqmjpsTrDubYDZa/Ek+8KXTsJ7XHDDu9HTx+GPY4D
l05Bl48joR5oSRjW+wEZSQdHs6ChTHAgDRrMAEezyb2a0RxorAAaLyI/ghop
REZLEfKe51Kktwjpyierko4CqJ2oTT7DbTlEKALb86AvBWB7IdheBHaUQoTa
SqDWEvhLJdJThwy2YCPt6GgH/NcrkfFuZKIHmSBHdLIfmRpEpocxIpSSAXWC
yKWUuUna7BRzjqgZZ+hktbjA+RtNRf9KbHWZiKZSK6uSq2syq2vyyysKS0uC
xSWD+QWjmQXTtVk773MqEurqyvoqipsF8ptJK5TWV5bVU5bVVZLWUxTVU2Zr
ybMEUkwlcYYCn6kkwVSVZWspieiqcjZriBrq8Iw38U30xE0NSTe0MJa3NFG2
MFaz0NUy091krK1jqObtKx+ZLBmXxv+Qzk/M4iVn81OySSv8kCGa/ImXlEn8
FE8nsygRRMXyCAZLpYrLpUorJCpIExSpKWdXl9FqyggMac3V1LZavLMB7yK/
VaMQGHZWw11VSFcl0lmBEpPeWiL8o6NN6GgjeYaCAHCwFBko+HvpfSr8JR5s
jQJbIqHGcLDxNdAcDjVFwM1vkf9L01uHtZV9b9/knC3nxAgkJITgLoHgTn2m
7Ux1alOX6dRm2qm7u1FaKtSgxVqKFHdJCBA0ENyd6szv+31e+//dh3me61rX
vk5T2j/afM59r73XWlt3i846SiVso++upe6soR6s56Uehq9/5z3/lS6/zNfH
4ZwT7LtDzLPN+M5ySIh7uxcSQTwdSR3wNnu8BacekhyKpndoqOV21BIVPU9m
ttQOrvAEoQpaLeYtsocb/PnzHBhnoVmYg8WJtd7pV37Y/qODnA8Sz3hPZLt1
ZbvsnMe8/hMbX5sXP7VfpMHro/HuXyyXaviPjzHZd/Clfczr8+Km99KPLyxf
n1M058hf35HdPSKqTnO8dU6+fTVzeb9ji37no2vOLy7jvJeiC8ckOzdYHdvF
ZCdYPr5qefWETfpzvwsHLUiqtSaSPbhBos9wSDiv+GutVdlTqbFA/dsyYeJJ
OFASGHfE5tx6SWeqUp9gf2Qhk3RY9GCv+eZIHOkEVwbSainwkMK5XkJnc7g+
WKC9IhtLVVbdVCyzZZY64AMBuPSaQP8Qpm4HsTGg6AjueAg7H9N9SfySIzh7
I5W3mTZcxUMpSHseN1zF2pOs/hSuPMkcDkEbvGDSIThRgv7b4dOV513z2q3q
mUD3mt+cwnZl8fty8UAhHCnEA1ylPTeNZKSA/DCcKkMzZcw0eSiFUyVwsgRN
kodyOF0BpyvRdA2a0sGZOma6Hk3UofF6PNrADNWhPh3oJW/sKtRRiUzVqKMK
tVchYxU0VtLcm1zPdDcwPY24t+nfCuTZ4wkTGOmE3OlhP5oYRLNmlSUp4adx
4afZTZvP0+ZfPku/fpX+i9534kL/lv3zN2dECYPfZzH8+7vq+9823/9Wffvu
8O2789cvrlOf1VMzMdUVQTcuuMYsdLQPVBMAXYI8nQI9nIO8HAPdHQPcHP3d
HDSucn83qdpJ4m4ndlYKneQiZ2uxG5FCJwtfF5m/p1Wgt1WInyKMYBikjAiy
jgxWRQbbRQQ6hGucwwnF7st/dX782uZFquL1O6tkAl2WPD1LlvxBmpJpnZxl
nfZRmZFrk1Woyi7mRLCgzLqwTFlSqaqosqmsUlRUWFaWi3XV5nVa86Y6UUuD
oL1RaDKwXfVsZx3bWcuYapmOWtyhBSTXHmjEA03MYCMmOfhwHTOoRQMV9GAZ
PVSE+ogzyaBIvtCRCoxvgDGRaksEHW/p7hSq/TWtvUHnHKMzjvIyTtGpx3hJ
f/LeHORlHucVnaWy/zBL+41O38dk/YHrYvkVtzGhL2EL9fYP5v46+uIC+mwM
73gQVXZB1Z/ulHFctm8uvcqeObVEdnyF1cYIi2Aran2A4t3VgIybnruWWDqK
eNvDpb0v7f5bHf3qTKCKMbvyC6q+Km5PsfklmL/QA22ZI1gdZrE8Ulr+RDmi
9bn0u2pZqPDoDvuti0SX97Cn1uIzu+C1I/D6PnbPKvHGn/iv7nm9ilP/uU31
+BJrzJSnPnb+aws+sEF8+6h5u8494Y5i51r5ihj86CxqLfS8c9L8/F+ax3eC
j+6QHNmAD2+ynOdhRpTl3kHBYjXYv4J5cRzuW07N88TP/pJf2AiXRwAXC+xm
Kby52/bqLoUUUWp79s7vDg1v3e/tkAcKwbNdkqoLzLWf8RyF2Rwp71dHeGUR
k31UVH0Jay9j3RVcdxlXnQJlp6nSoyjnVyp7PZW7g269S3fGgvJ9PP1J+OJX
vNIWRMjpJc70qz9xYyzufm7Wlyr41ho2UyEdyTIbzwNjxXCsdDbK4Hg5Givn
pnWNVnEtS2OVcLIKTVUjsk7X4OlahiOuDk/p0ZQeTNfCqVpIAJw2cMMuZrgx
a8yXNuazCX7uxDOdeMqERoxg2EhAw/0tTFcj7m7CPc2IrL1cew7D9ccZMXGn
g+14yMQMdcKRXjjOWVOGuNOJQTwxzE6O8afG2elxooOCT9OCz9PCzzPiTzPm
nz9bff1q9fUbWWXfvlp9+6r49tmaW79af/ui+vJJNTPtPDoRMDE8d/c2D2t3
T+dgN9cQT9cgH5dgL9cQH+cgH6cALweNh4Ofu4Ofh7Wfi5WPo4W7SuSkEDjK
hU7WQleVyNPeQu0s8yNO1UsW4i0LVcuJIBISw/wUod6KEC9lsIcy0N0nxvXc
DdXT15ZP30hfpli+eW+V8l6W8t7qbYbiTYYyNUf1Pt/uQ75NVoF1Tsm/u6Oq
4nKb0nJFaamstNSiotJCq7Wor7VobrBsM0hb6yVtemFbrcCoF5G1Vcu01zJd
9UwfQa+FGWwCQ41wqAEP1XJ3vvSXg8FyPFSC+3Lonky6+wM0pYP2FLo9mTal
ksyd15cBOt9g/T2idHTpXWB4Dauf4uzLIO0keHMQPdsGE3ejrCO8tzvNMo7w
0w6ClL2g7Dp+/bvZjR/NHqymkw+iK4t4J8J4ZyKpsvOiqQ9uhniL7SFwT4yo
4qqbKTGw7L5qoT11MMbS9Ezxvcz7+UGFu5D3qz+/8LioO1lz74Ctis+b40Gt
9KL2LLCI9rL+/WebzEfBd4+6/BLB1MSKRotVD09b718lMeX5FSV7Long3zgq
f/kgdHmU+f61lnHXVD8ECu8dlZhKXN/cV5zYIkq+KX5wzuL5Lbudy83jzor0
afKnF62uH5fdPmFzYiuKPcnsWELdPGA/VB2W+TR4x8qwpzeWXT66YONiq1Xz
pJuW2cUE2O760Xb3Mpufw6QhTrL182yPbbANcRVe/s22I9WjI8N7qTMKs8XZ
5yynMxz7ku1+8QbL3UXrPFComJpjT/3izl9rB/ZreGWnRJ13RINv4UgWzNhC
ZfwKklej1NX0h3UkqJxttP4c6oyFtSdg6yX6415w8yf20k/8a8tB0UWUdxyU
HoMN13ijWfzBD7gvje5/D/szwSCxnblwMA8OFcKhYnqkDIxUAq5tsGL2oQpO
VINJHZyqRzMN6HMjJvGlCX9uYj414U+t+HM7njJyU2VmTPhTJ/7Shb724K89
6Fsv+tJNPkSTRjzahoYIjAS3Dna4Cw93w9Feonrs2CAmMT5McGMmR5jpMRKc
/H2eFH+ajZlJ0Qx3bGFOpPATUcNPFkQQCYCfvij+jS9frL+Q9bPiM4lPii+f
rL98Vn35bPfpi/PX7+qR3pClC9wdg309ggPcg/zdQnxdgtSuQb4ugX7O/j5O
Gi8CoIOvp7Wvo8zbVuJmLXSyIgwKnBR8ZxuRp51E7WDh5yIljjTYUxrqacVh
6KcM8VAEO8sCHGUaJ5mX3brfrWMfWz98IX/2xuJlsuxNunXSO0XSe+JL7ZKz
bdOJCObZZuTbZBbYfCxW5ZfYFJTZ5hdbFRZISkosKiuttDopV6KmtzDoxAat
sFHHb9GyrSSqGWMt7jLgvmamv4npb0SDjWDIgLmCpWowUAWHKsFAOewphCQx
78mBXZnQ9I67daIjnaSEqOs96E4HLU9gzXVae5uqfUJ3fOT/06jIjnVdEy5e
pmF/VrMr/dmNYZJHB6PL41Wfa+XFj2x/9cHbg4XvLnp9OCF8vZlKP4hf/Ybj
NrJnInmJO/ljhYqmVMVie3q7rzB/r3nLfcXbg0Ifc2pXmKD8KNv13Pr8WtbV
0izEhtroj7bPEf7sx7c3p34Ol62d6+aiEGtUotLbqk8FNvq3dmsihBc3Cy7s
kG+MEt3fL+z4oNAnW57bKWlIkQ3qYi7vUWU/kHZVOh/eLrz6p7ToiSDxjnLr
culP4ez9w6L+SvfCVNcdS5kr+5lNi0DJM1lPZUDceceDm1XR/njHz9SLM/DG
YfutS1Wm3Jju6m3X90fmvFjUW77k0XHvxDPWo8Vhby/ZrQ2R1Sd4zFRF3tip
PLxA2B7HTmQ7n1/Ll5nRR5ei0nNAdxddXc16YDNPwNsSJHq917LhvmPcGvFu
R17WXlB3Egy8hJ2vceY2ULjLrGgfVbCPSl7BqzklaLqB6i9D03268z5ovkH1
3AND8bDnEb/7MW68Aepv0/W3YUs83Z9CD2fQXIUMN0wGDhEAP4LBXNCfxw2y
IDGYj4aK0VApJq/ZwXJEeCQkjlSjsRrM3XI+20c/Vst1EY7r0YQBTzajmX9n
VpjwTDf81IO+9DJf+vDXfkzWzz2IsDnVwYwb0UgrHGyFfS2gtwn0tqA+ooMd
3Dn+aB87OkCQZCaH+RNDgolR0eSocGJUMDEsHB8STI6KpicsZqasZqZl01PS
abJ+sSQkfp4h6NnMfFZ8+qz48k3+7bvNP/8o//sfm//+j/30qEejPuDCqUCf
EI1nmL9bmJ9biMYjSONGIlDj6q9x8fN10fg6+fo4qr3k3o4yTzsLVxuREwFQ
yney5DvLRZ4qc7W9xM/JIsDZItidYCgP9pIHeSoD3Kz9nRV+DlJPB+9o+flb
tnfiZQ8SrJ4mWr5Ikb/iGLRL/mCX/tEuPVf5Ll+VnmuTkavKKrTNKrDJKVDk
FsoKiy3LK2Q1NQqdTl5LGKyRGLSiBhI1wmYtv03HduhxdyPiGnhb+ANN3GxD
7gZekgbWon6uThv3VsCuItCZR3fm0N3ZoDMLGjNBxwfQyQVtSqdbXsGau3TF
TV7NA7r2CaV9CowZ/PESyY3dVu4SylsBNTY40hWtUDO3NjoU3ZL0ZvOTL5j/
4ML1kr86qMr+S/R8A/VyF0w7LOjJJgaVidvGNqVKG16Ljy9EG51A3DL0di97
YC4IlVI/2vD2hYPzy83XBiIfqVmQCrhaUPaYZwt4/vaiDxd9xwsjiuI9oux5
V9eZFV5TvTqjCnfmb1oifXHG89xe9z1LhLGHzXcv4m+ew8+8zuTGiZ+ds3h9
GmfGWp3YabN1qcWRrSjutJ0+2+/OMcu7h9nch+yzc9LLf7nt/sV6VST79CST
/cjy8Hp+8Wv7kmSXQ9uUO1aploeAJQE44Tg/7Y7/gVXK10csuz96X9xsfmOd
wPjaKuEv8RwH9PG0vC/VPveaNEoOr6/l31zLLnI1kwGzIBk8sVCQe9G6Pc3z
7k7FJl/89hjb+xyPvpQ03ha83ozebsZp60DLPdD9FGnPgOqTVONtYLgJC36j
Ox/ze58BwxVewyW6Nx4OvmBnMtHnj6j5FjRcIz9GN8eCtsd0ewKvO5EeTEfD
WXjk4+xVgwVwvBhOlMLJCjRRibjpQMVwqIRroh8u58aVDFUQAOFwFRjVwlE9
5voHuXGXYEgPR/RotJ7ro59owhPN3KHhRCsz3orHW+FEGxrvQBOdcMJEAk2a
ZjvrOY+KJ03MWAe3QUqUsa8VdbegrmbY2QjbDUxHI+xuhb1ENDvZoR7+UD9/
aEA01C8eHhSND5uPjyrHR1VjoxbjY5KpCdn3Gdn/fJb+81X2ZcZqpN++ud6p
OF/15o3D1cueG9b7hMR4ugQG+kQEqsOCvMICPEP8PYI17kF+7oH+bv7+bhp/
d43Gzc/P1dfXys1W6mojcVGKHIkOWnIMOlkJ3W1EPnYSX0epxkka4Czjtm5c
rQJc5BpHaz9Hhdpe7qbcsEt686HN7UeK2ATLx6+Vz5PtXqbYvXmvTM0m6KlI
Jvgu1+Ydt0dq+z5X/iHX6mOhvLBUUVZpVV0jr6m20lVb1lVL6qtF9VWMoYZp
1eOOBlF3k4C8nXpbGKKAXMFtHRjQg34dCTig4zo0u0pAVwFhEHXmA1Me1U2e
8wmPVHce1fORak+BNbGo6DKv/C5Bj9ImUFVPYOE9OusKyLsF4/5AF9bQl3+l
7+xECfuZ1D/hu31mSdvM0v/Aj7aixzuY+A2C51vogtPgyXa4zw/sdgO5ZxjD
S3B4EbUhQHBhCRu/Ce/2BVvdwc92dIwlXKjkxSjNIm3MAsRm/uZme+fJ0s56
ZN8PP7Le3lbAm+PAZB8SDr5Etc8tgh1QuBM+9Yvd1d3u83zEH67KpwtUnTnq
pWHCjQvkD895bFwoXBMND/2suLrPZsuP7K4l5hUZq87vV8b4i95cNm9OkWbe
tzq9Q7A8ht4aI2x659ReHnx0p+XaKOa3n/kndyoIm4VPrC795lyW4luW5Hl8
h/lcX+HWn+1DndCyAGb/IjTH3ezXSMnxFfz5rpSDhLc12vz0UnZ7DPB1pFQi
SkqDBe6WC9Qie4a6vlYy8NxqNMurO8d2stKl9IpAdxUYruOmG3Trc/bREhQ3
H+hvoarTvNrrdPc789GPuOEyVXOabo9FdRdp40089BgOJcD+OPrvAvz/NbHd
r0HzfcZwD+vv0rV36Zq7gLwh6x5Qhse85uc87igwHXRnwH+Hi46VoYkqrqGJ
xDgXs+MrqwBhcLQWj9UxI3UMQW+wFvbXcFVSA1o8YmCm2tgpIzPdzkx3IJIJ
fupCn7vJAzGozGQ7mmyDRAHH2tBwM+D6CpuZ2e5COGYEnIPtYqe68Vg37u9k
ejoYUxvuMjK9HWxPBx7o5g/2Cfp7iEQKJ4eFkyP8qVHlzLjtl0np+JC4q1lS
ma94Hmd//qTjbztcly1Xh8z19g72dw8McgkMcA4J9ooIUkcEeUeEe0UGe4UH
+YQFeYb6u4X6uwYHuAQEuAf4e/j/y6DaykkpdVJKHBVCByuhgyWRQgFh0M1a
7G0jUdtKNY4EQI5BAmCAs7XGSaVxtvG28whSHDuvuBEnux1vHZugePjKLj7R
NiHZJumdKjlDlZxpl5xpm5atSMtSkPV9niKnkCSDypJyeVmlrLJSqq2ynN0L
ZRpqBE16YbtB1N3M72nm97bwuxuZnnrUW4f66uBAPerX4z4t6qmCnaV0Zwnd
XYZ7SnF3Keguo3uIHS2DPcWgrwj05zMtSajyHlURa6Z7Rte+ArpXgBsjc5fK
vEZnXeS9O0GlHKdSzlLvL1IfLvDSjpsl7eUlbKXi1sHnu+i7P8M3W2Dsahy/
HlY+gKfn471+9F9hvLNhIONP5uRStNgJHJ/Pf/YLLjonzjlr9e6CbM8c88Vy
akeQZIOfaJmaHyWl726y6nmh/F4e/nCPtb3ILNAWHFiEz/6IDvwocZCAK9uV
xjTPiZolm+ZYXF1Fa++YFzx03r/SIv++23hNQMpdpx89mNxnNrXZPr/9rIg/
zhoL7OqzPTbNwxd38x8fBic3mqfELVo91+vgWmFFnECX6PnyokPFe821IzZz
fSXrw+HxTcymKJR9gzXlO51YK753yLUlf+ndI84rQ8UvL4a8vOB4Y691sI1g
6yLV3p9VAfZ8L6Vg83zVlh+l9mJ6ywLzkliX8ljrZS7MjgCq9ISo7Ymg4BTS
xsvvreM/3kDnHUa1t6jyq/zU36H2hrjkCMzdjVJ2w+Zk/nCOqPQwbH/IdNzi
tV9DXY/gSCIaiBMaHzD1d9mJIsGnUjjxAU3kcEcMIwXc1Kbej8iUw7S+x81p
0JAMGpKphrd0azrs+AA7s0Av+ZkSPFyBRqrQKPGfutkxerXMWB1RPTisByP1
RATZ4To0XA8G62A/+Z40wJFmNNqCxtuI4cTjhLsOrnV3yoSmO1lO+DrRZBce
N+FRIxxuBcMtcKgZDTSiAfI3GOBQIxxswn31bK8eddRAYw3uJIpQBzsMqMvA
76jnrl1o0gqrC8XZaeJX8cobZ51273BZvMw7KNrPKyTANUTjHqb2iAhQR4b4
kYjy84sK8o0I8g+L9AsL94kkUhjuHRbmHRrmFRroHhLgFhjo6h/I6aCfxs1X
46r2s3K0tnRUmDvIxQ4ykYOlkDDoLBe6KCQeSsKghcaB6OCsCLoqAl1VGhd7
PxdbT/uw+fJzN+xuxCnuPCY6qLqfoIpPsn2WrHiVpnidpkh6Z/02wzo5U5GW
o8zItyNeNL9YVViqLC6TlpVZVFZIayrFdTXi5nqxscmyvdmis0nUbRB0NUBT
HeqqE3TrQI8edddy5/Jd1aCzEnZWEBFEvZWYW2u40fd91VwRb3/1bGKYjRtf
QF083fAaNqUAQyqtS6TK43lF96jCO1TBDYow+P4ylX2TKrhPFd3h5V2m0o+D
xP3U69/M4lbDrEP828vBrR9Rwq906j70cgc8P4e6OB+ejqBvLIOJe+hHv9KX
F8Iri9CbfajzgXDghdKUwFxcD9d6Csvvera/dk8+LYuQ0Sd+ZIqOouantm/P
23hLzdzMeT+ozQ/94npsi4uPgr2xQdz8QDBd7H5ii3W4PT6yXHZzl+q3Hyw/
nBXWJVpkP9Dc3iereykarvA8u11xaYco567o/l+is3utty4RRzmD+wcl07Xz
te/Dt0Uyf64U/LlCeG0b6M2UVb22ObrdOva8/6bF8nn+ogd/uF/aDn4KQE8O
mA8X2qWftz20gO15Z/93bcS9363CXNiGp7ajH/3v7nE6sUqif2JXdEs5RwWO
/iTUXhK33hWdWABj5PRGN3g2hnm2jdnlS612pi4sZt9upwtPgPr7zFAmbH+C
UleAzJ34TDS6tRzkn2KNz8BkJtN8me65Q1ecRoeDmbXucIkd2BsMtc/E/2m1
nMynJwvBRCEay6eHC6iREk7dpvXMdB1LjOWwnpsC1F0GOotARz5oz6fJ2lkA
e4txXxki6f9gDRzWgbE6MMFNLCSeE48Z8LCeGazFg3V4uIkrjBkj6V47muiA
4514vJMZ78JjJjzUCmdH86HB2RKaMSN/1MgOtzBDLYhkhQPEczbingbca2C6
65FJB0zVsK2U/fCIvXDQ4uAe5R+/W+/bLd++zWrNOpsly5yj53v4hXu5E0sZ
5udJHGZkqG9MsG+Mv190kF90sF90oF+Uv19kGCHRJyrQNyrCJzJUHRGiCY/w
i4jwIQyGExKDPYODPAIC3f0D3TWBbn4aF18/F7WfxEEmdpSKnWTmTjLhrBdl
XeQCV2tzdxtzH3uJr5Olv6NVkKtVkJsywNXW38XBz8HO02nxcvmF2/LrD5R3
n6ruPFHGPrd+mCh/8kb+IkXxMlWR+F75JtMmJdf+faHjhwK7nCICoHVxiVVZ
mbSqUqLXWRrqpM0N0haDeZtB3FbHJzlgp54x1WKTFndylWmoU8sd7nRWw+5q
yNWI6mBfLRwgPqQBD3Hjm/BgLRgm76tcZHhDN7yEhkRg/ADaMunmdLo+iSYu
VJtA1zwFFQ+p8jiq/Ald9RzUJNC6eIpoZcFVKv0E9eYvXux6fP1HlHMSfjwO
EzbR13+gHv4CEraCOz/Rl+dSd5fR9S9RQyJ6sx/fW0PlXhUNFMhbYwXVZ/l5
J8HtX8HvGlx6XDSSaJV7lgmTgDm21GY/+GCHtO6p7c9qqLZg3x+TT+V5jOf7
/aBhFrmCm+vx2ZVCXzvhcn9x/k15e6rs+WnHGwe9ji9nr/0m2zSHiT+Abvxu
fnGn9bwA8ZYlwmNrzI0fnAsSbVZHCK5uQUX3BU+PSjJiXdJuey+PsN4QDRMO
oXNbmKTT1uOlLmWvXY6slxW+DLu42zra02JdCL69Fe9dTP3oKc85qyy5Ldq/
CKutQOZh1BovPb+C2RbGlp8yzziB16npVX44YQv/zjJqnTflZ0GHS6gFFvD8
T/jCfPrUXDr3rDDvIEzdCPIPodKjqPwYytsBCvbDaz+CR+u5neeOOGS4BGvP
gp7bVMc9/PI3/vFF7FZ/dm8AzjxOD2cxox/o8Sw0WQCnitBYIRwtAsOFaLgI
DhXRIyQN1LLTDcxkEx5vJoHGW/CoAffVgM5y7ti9vQSYuO4Y8gZGgzpEnOew
AQ8ZEFlHm7gpMSPNcLgZjrTi0TbMkdgFJ/vR9BCaGUXTI3hyAI31oKF22N8E
exu4wtHOetxtYLgK0kbUyx1VoK4m1NmIjHWwRQdadLCuRPD6iejYccXcxU4q
f0/7ALVbuNo1ytcjSuMVo/aO8VPH+PtGB/pGa3xjAtTRgeqYQG+yRgf5RxER
DFZHBZHwjQzziQr1iQz3i4jURETMRrg6PNQzNNg9MNAtIMDNP8BVQxj0dfLx
FTlaihxlIiepyEkm4DZkpHxnucBNKfJSmfvM7o5ydtRVHuxhE+Tu4O/u7Ofi
7OX0ywbri7dlV2KV1+Osb8fbxCbYxL2SP060TnijeJmiSMq0Sf6oepdvl0kA
LLTJL1EUlksrquU1WkV9g9xgsGyqFzfp+I06pqmWaatjuJKYOvIigu3VkDuL
r0KmKtBFDH/tbN9uHeyrRwMGdrCR/d/XT+jRQDluewfqX9LNybg9C5ryoDGb
bnlHG5Kh4S3dnAoNb4D+FVWXSNelUg0ptCGJ1/iSp3vIq7zDK7jG+3iZTj5G
H4+h/vI3u7MEvt6Jn2/jPVzLi13JS9xEP1wHj0XQr/cKCq9L4nagPRp4d70g
6Rhb/UhydxNKWIvPzgeHIuEeTxC7iMrYzdxYzj+4gF3siAJsqVAVlbBTfmqd
ubsQxG8A7bFs11vXXyL5bjLa306ySKNaEmW33F9UdVnQlcpPOifxsebf3qXs
K1Qf/NXcWwZObbY0ffQ6sV3iLKVjDzLaRxblr5SPT9ptnStdHkif+MW8M0n1
We+beNFpcYTt0kBRjAcvdp+8NsE2+bzrsaWw8531RHXYoZU2G360PPyLalWk
LNBZuG+xfFOwNMQW+tvDVWqS3gqWuNLRLuDaampPKB2u5HmIQIwK+ot4aj4v
WEb9qKAT9rL6+zjrD5y8FWbtpPP+ALkHQe1t6sNOmLmTqr0AtCfoxtvYRPK+
JJ7hGpWxCVSfhGPJ6FMG+H/K2P/ksZM5uOk+NMXhngTU8YDqeQH7UwmP3A7M
RAkcLQYjpdxk5v782dkjeVR/ERgqg2M13KTQmTb8iZsOyp/o4A+0IJOWNpaj
tlLUXkYTR9Rby/TWMz21THcN55T6GtBYOzPZxUz14MluON7BjJkQye8m+/EU
IXEEfR5Hnybw5DAa7cf9Xai7DXW3MJ1NDLGaHQZgaoIdTZhEZyPb0YhbGmBL
I91iAMY6UFPEv3dDumq1yiPM2ynC121ugHeMv0+Mj3d0gG+Uv5rAOEfjw33i
70MYjAr1jQpRRwWT1YdIYWSodzTRxHCOvsgI/0iOxH8Z9AgOcg8K9NAEEi/q
ovZx4Rj8lz5iQf/dFJURBvlu1kLP/82gpcZJFuAmD/KyCfa0D3Jz8Xd3U7tv
2Ky8cEt24Z7yygPFrUfKWUdqFf9KkfBW+YqkhDm27/JUHwpsc4ps8ousS8sV
VVqFTq+or7eu18vqdaL6atSkRW11rLGe36bH7bXYSADUgo7Zineigz11uFeP
e/Swpx4MNBFHwRAYBxu4STKDWtyVy42qaEoFHTmgq4jr5G3LAa0ZqO09t0dq
zCSOlG5Ko1s+gOZM2PwONCfTzYmg/ilV/YAqu0uV3KWK71Bxa8yOB/LOzqOP
z6d2R8Irm20+HDd/sY6OXUEn/0Ev9wYH5uJLS9FWZ942T7jNAx4OZ3aE4Z8d
0emFeJ8P9acfiNuO9geiXZ54RwDMucReWAY1crjAka1/7Hdrs8iez51TXFkF
N4UIbMXAQ4ZidzsNZARUv1SH2gtP/cS++sN8zyLLCG9x4WVhb5rq2QlJlLfF
u3PytnSrgkdWP6j5G8LR+fX4xka2J8+rI9czxgNvm8f/cF6YdQXd263oyfMt
TQpeGCib4y5eEynZssju0E/igotM1nXJOg1Tckv5vUKdfdd5dYCs4pFzS6r/
zd/dnWU8OQYODO1uaeZuQfvL6Qh74Ks0sxOaOfHN5tgzhxaJjy9mt6ph9gXz
5liB7hzd/Qbrr6OSk6DyAqx/AKtv4pJTcDwb1V0DGRtx5UlsfISNcUzeHlB2
DE5l8acz8OgbMJFMfc3B0+n050xgekrrrvAa7lDGZ3RXEuhOoYayOTUcKQSE
xOESEojwOEjM50fQ/ZHu/ggGi/FIFTOux5NNcLoDT/Wy413MYBvxjYIOrai1
gmotpzqqYKcWmLRcb2mHlqso7mtCwx3MZB8zPchMDsLJIXpiAIz305MDcGqY
08SZca5faXQQDXTTfZ2otx33tDE9RrarjTFxW6PI1Aw6mlE7IbGZbWlBHU3I
1Mo01QiePxKtXGvrHuzsHhbsEeXrHaVRc+hxmugZo/GK9ldH+vtEBpCYFcEw
34gwTQTRwTDvqHC/yEgCoF8EEcR/dTDEI4hj0E0T4OqncVarndRq4j9FzjKR
i5XQ2WoWQBmXDxIdnGXQwtfR0s9JGuiiCPGwCfayC3HjOpv83NdvtTl3Q3b+
tvzaA/nNB4qbD+X3nygevVA+T7NNynJIyyUW1DGr0KGg3KGixk5ba1Nba6XX
WtZWifVVXGF2c52wpZ5t0SEi/UY9ap8tECVZcFcD7mlkehuJP4e99Vym3N+C
OdNej/r03BS1vlLY+gFw9H0EXcWwuxSbCkBLDt2WjdpzoSmXAEi3pHPotRIq
s1FzBt30FjS+ouueUDXEiBJfGktVxNEpf1KJe4T3NotWecFwG9pTDLZFKRL3
W91dSt9aAh9vYzYGMNeWMa9/RydjwB4N2O3Lu7QI/DEHHlvKPN8rOxZMX51D
l5/DRZcskg7AKz+hJ+upA/NBpC2KW4ZND+QX1ordhTwfBV6mlp7e6rP+R5kj
Rvc24J5H4s40+xhX5K3EmyLFby/abAgRPz4gubEJfriqenXe4exy5umfzJXN
grw4hwMrzINVOG4P0/5C3JFlHXfCY/181Q9ezPpQeGs7fyjFfLTA/8ou9/yE
xU/OeyzyFcR4WS71hqv8QbgjSD3E73ojzbpo/qsf1t4QTWbbpp+zduWjP35x
unXA7fgGZZQrUrC8uW6CFWEW0W58Fz5vayCuuCBuvSdI2IE60yz63ljrTuNP
xbDtJf6wg87ZCQoOgfRdOOM31vgQ5e4EaauoV0t4Kauo1luw+wHI20+NpvG/
Z4GZN3gyCUwn0J/S6H+qwNcKYe9bYll5ulu8xjhofA47k6n+92goGw/ngpF8
OFiIBgrpwSIwUMLNpewrhN35dOdH2JnLlQEPVMBRPZxsnT1T6BJN98vHOgUD
rbhLzxi5Lm/QWgNaqkBbDSIZjamOWE3YRwxqN5oYZGZLzuA0iSFOEyeHZmEc
ZSaHmbFBdqgX93WAnnbYbUTdRqannentICvuMsLudqarFXa0og7j/94gNRqk
964rf1zm7BLh6hqq8YrSeMf4+kVqPKMCvDhZJAkgZ0H9okL9iPZFhgdEcvLn
S7xoVOS/IugbFuYTFuIdGuQVEsRhSOwo50X9CIMsZz5n0XOR810IhlYCFwV3
NsF5UftZHXSQBjrJQ9ysQ7xsQ9ydAz3cNYRB1ZnrsnM3pJduSq7eldx4aHX3
qfLxG7ukTJfUXBcCYH6pQ1m1faXWulpnqdNJarUSvdaiTsf1RzRoGQNxoTqG
MNiqA8Z60EWceQvb28r0NKEeA+ppYvqa+f3N7EAj09+AuVFOddzwipYPsOUd
JpLXXY67y1FnCWzPB0aCXiHqKkJGrpGQbs2CbbmzVbs5RChpA0cflwbWPKYq
H1GVD+nyODrrNP14Pd2RYdlZ7LImROJugVf7w0s/wnvr4eONdOEZmLwfP9oA
bv0Erizg3foZXlnEe75LXPfEsi4OF54Hb7fzbq+At1cyD39ADdeg/hZ5Bqfm
Ui93som78aXlzAZPwWq1OEBG/RYprrtl/X9VRZc88rHj4zW+dMo+ELfT0lHG
+trwP15QTHxUJJySOLP0+nBW91A6U+55dpsy2omf9JdoLM+2OcVnvhd/jhO8
to45sJRNO2k3o/VLuemlUTC/xaDE3/HdHcyp5RZdr6TT+a6399imXp//5qrn
rwsVPgoUqoS7Y+hd85kwJdgZCG+vxYcWsd7m7NN9ss6n1v1vFH8uFdqzOHan
svqOS9ENh6VOcLEtzvgDVZ4Gj1bSZxaiYwtw7nFB1zOYso19vZZK2cBLWkE/
W0qlbKXbnyDDVSZ7Gy9rO5W3m264gmpOQv0pMHAffvqAhp7gsUQ4msa2PRW2
J+Ca+6z+iWCygu3PZOsfmdXHA8Mzuj2J7stg+jJhXxY9lMfdGjlUREiEA0Wg
rxgMVuDBSjRQgbuKUXs+bMmmjfl0TwUc1LOjTdy250QPnCJKNwDH+rlD9k7i
KvWwTQfIm7ydGKpa2NmAuxtxXysc7EAjPZjwODXMTo8w0yNoehhPD7PklxND
zNgQHh1gh/sEvZ1sewtqawLtzaizjenr4g/0Cfv7+L3dmMRAv3B0WPRpQjTY
Yf7urXTlWnvHQG/vCH91tIdXtC+xpmpuTybMNyqU0OcfGeU/az5ngzyE/5sP
qsPCfUKDvEMCvEOCPIkX9ffnDibUame1N+MqY12tuHCTs64KLogR9bAVezmY
+ziaq50s/ZwtApylQW6KYA9ViLtDiIeTn/svm1Qnr8jOXpWevya5eNPiRpwq
7pVrQqpTSrZTdrFzUbmqrEJeUSWtrJLqtJZ1tZb1eou6WpGeAKhjSRpo0OJG
LW7SESvO72kT9Lay3cSQN9A9BtDXzI3XJiR2NxBHCvv1YECHCGWNGUTa6K4y
0FvNdJYBYyFlzKPbC+jucthdho0fieqB9jzUUYTai2BbFuc/OQCf0tVxPN0T
UP0YVMVzDOZfAc+3msVvAhWxTP1zyxMrRSvUeLHaMkDBrHRnXuxjUw/B9JMw
aR+8/RN9axm8vQQ+20DnnLHIOeue+LsobT/KOkESQ/h6D3PMn369AVRcZU7O
oa4sAOlbYdoeuuSseeUNx7Yk579+ZNa4wKI/eMMvrYtvubhYAFdLuDNCmHRU
dWK9zA7wrq9nDbGC54elahuCJP3+MFMbLzm4xFwOqFubUNFlwav9qpJ4t80/
yGz5cGWo+OM54fA7K1Oa3YHVzhsXOvsqUIiK3h4lLrhim/QnvT1MXHvP5VuF
Y8UjF38b5pd5DiGOwmA36GsPVHzGVQjcpWauYnB+tVXxJa/Kq9Jd4YwDpC4v
RYV/ofJTcH8IjLFCN1egkvN00ja8xpla4gAebqQa7qA321H8cip9I52yjpe4
gq44hZvuUU23YeZ2quQgrL9CV52E2Vvp8r/oijNo5AWTvhXlHhOMl8teHGSW
yOj5luDsCqozhf1/O8STJJvLAB1vYfsraEyku9PpgY+wLx/35tH9BQRARIIk
hn1FdH8xGixjBqrwIHevAdcZ0ZJDtX6kOoj5qcSDDXxubG8XO9FPyMKErMkh
bnJFrxGbDMioB0Y98VewvR6317Fd5OvUBns74MBsRShXlc0Vp5EMEY8PI4Ih
R+IQMzTA9HZhon0tDYAEgbHLyPRzx/SC4QH+xKj5zJTsy2eubLunVXnulJUm
2tUlSOMZ7UfyQTWRwugQ3+gwTRRhMJyjb5Y7/wgC4L8MhvsSBkOIDoZ4hwR7
BQYRBl191SQfdPLx5rvJ+e5ygTtZCX1KwqCAiKCHvdjbUezjJPF1ttS4WgS6
SYMJg54qrvve3d7X9ZdNdscvys5clV64YXXpjvWteIeHiS5vM+xzCm0LSuSl
5RaVNbLqGkVNjVxLLKhOXFcrNug5BayrwnXVqLGWbWsStreI2hsFbXXEhYLu
Bq6UndjO7npCHyT09dVx8wo6S3ETMZ8ZsL0YdVeh7kpgKgYdhWRF5LeIGpLn
tlyqvYD8ANfZZCrh5ju1vOESwIaXdG0CVf2UV/OEqo6nqx9RBVfBy230g9W8
u6t48Zvo1wf417dY7lnmtdDPwU8lenLC9nO93R8/4AgFPL9clHOGfbEF3l7A
e7yGfr0b7/PnbXMASbvB418FxVf5b/8Q7PMwOxuCEveJjkXT1xbQT9ei2LWC
1I2w6wH75b3tuVVsgIQ+EU5U1XxnhEhKmXkI0LOd8sl0q4bnVl5yOlCJtoYw
d3ZaVjzx2LjEd10of20IDLUVBjrzwx3hai86dpvFZIZD7wereW60DFDHfkJ5
p4Unf0TpZxw/VUU/POLkqWAWuEkWOAkXe1Or1GzKH2LjC9n9LWjHHEV3mnfn
+4CTvyjVChB/TJV60e3QapmPHEbZ4YUOaKUHCrbkuZvDrSHoZBQ8GALmy8EC
BXq4jV9yiX623uxUFDj9A07ew1adx2m7YMIS6v0GgiH1cR+oPIkqD9P6C0B3
BjbfpLriqcaLjPYYlfsnsz8I7fRFK1zo+D1MdyY7UiA4PAfv8Bc83oFrb7H/
dyvznwb8txZ/KqVnSsFUERjLhUM5cLSIu293eHY0en8BCdCXD3qLOCPaUwS7
C1FfBRrSoaE6pk/LtheD5ny6KZc2ku+DjulrwcMmhmSLk/3M9DAzPcqfGOEP
9/H7TfzOZtxej1r1oFkLWmtRRwPT0YhNzbCrBRIkB7rwSB87PsDM1osyE7Mx
OsgM9jN93UxnK2pvhq2NsMWA2ltwfxd/fEQ8OS37NKP4NG3+/bPF31OyqmLF
9l2OriFqj8hA3zlBPjHBvtHhmqhQ/0gSkQHhEf5h4ZqwME1YKHnwCw0j4RMS
6kUYDA729A/y0BAGfQmDzj7enOq5y0Ue1qy7NeumYD2sBZ4qkZe9uZejOWHQ
z0WmcZcFuMpmddA+1F0V4qbUuK7ZYnf8gtXJixZnr8mvxtrcT7BJSrfJzrcu
LLcqrbKq0lpVa6XVNZIarblOJ67VCuu4YA1atrlB2NYsaTWIWusFzcSL1gIT
Zxu4veLZ4wnEbRrXo84aYCpjGjNR3Tu6NR+YKlAXSb3LINcUVkR3lIJOYlQq
GAJgRz40FjPGEvIJ6CgG7dnAmEK3JsFGwuAruuE1XfeC0j4jGILi6+jVNurh
L7y7y3l3VvDurKSuL+ddXgXv/m51fAX/8A/8ortsX47w/Eb+HBvm9DL2/Z84
fgVzfzGd/gcuuSy6s5Z/dhn7fCPv6QZ4Koo5Hck/5kvXPROVP0S3V8Jbi+mc
E7jyFv/ZOvxxH2y6Y/3XfImvmApR0ks9RL+GWm5daOnMgt9Cof4abn7mPM8T
mZuZrdbIaq6Lx7Icc+64zQ1wDXDkZ910KXmkcLOCdubwxnpGf4t9f0J8aoP8
/HZrPxthgBJsChcVXRKNZzlmXrY9t8a59Y3b/UNOIS58N6lZmD08uECw0JX+
a4G44aZ4ON3u0i9MmB1fd1v89YOjMdF+oQtyFIGfNcIVfsIfvYXeUtpXTEfI
QYwSR9vwFljBfRqQthOl7wJPVtJ5h9n6a7DiBNPygE1bS+cfoA2xTEcCLtoL
yg9Q+X/RWX+CkqPcDWgt93DTOfB6HfrVk17pDNZ440PhsOGh4GsO+F9V4m/l
orEM4UQu+qca/10N/9HS/9HBf3SC/1Uv+m8d+5865p96NBvM11o0o4WTNWik
HPaVIG5kZQHsLIDdxdzkri6iodWQOxA0sL21THMJaCgAhgLUXApMWtBrQP0t
cLgDj3Pbofwvk5KZCdHwANvXyfa2s6Zm1KynG7WgUYta61ArYZO8+ZtQdxvu
M+HBbjzUQ0ypYGxYMD7CJ+twv6CvG3WZUHsrx6CpDQ/0sVPjFp9mrD9/ks1M
yKcn5N8/mU+PWj96oIpe5Oke5u8bE6aJCfObQ1JCkgxyx4LEfKpDQ/1CQ0km
6EvWkFCf4BAvLoI8AwI8NAH/HtC7+KhZFwU3ENONAMgxyHdXCrk2XkeJj5OF
2tmCY9BDGuBqwR0RuitnB18o1M4/r7U5ct7y2AXp2es2956o3r53+FhkU1wl
L6uRV9TIK6stK6rEVZWC6ipBTY1ArzdvNMiaGi0bDeKGOqahFjXV4ZZ6bGzg
t5OoZ9p0uF0HTMTG65j2Ckb/AVQkoZpU2JRPm6pwZzVsJ+azhLAG2gl9lbOD
DYtornOzDHEn+NWwsxx35SPje6otlW5Lppre0iSak0HTW1j/Cuhf8Crvc50R
z9bx4laYxa7kPdpAPd5GJfxGxW8ze7LF7MGvZlcXU3dWw0e7IVkLrrL555hH
69Hj9SB5H3VhIUrZj1vSRRNah+RDwus/oAc/UY9W07ErYf5Fcf4ZSdNDVHEF
5J2iE3dSV5bCnS54RyCMkdKRlrxQC3h/i9VwquvAB8+FnshdxNsRipZ5YY2d
KsZD4W3Be/wryj/L7lnAuCmkd3dZddzHg++UW6PFUj5tg8HmYLhRg8uvyP9b
7Z9yRmUlpLzkcN9c8HI/3hPKf75HOvhCPJrjsi1a6GGFA+yFzmLK2ZIX4SA4
EsNcW8MuduCF26EXW3DpEfDxLH+RKxsgQxkH4UCCTflt+xgrSmPFu7lOkHdW
+XSXZJWSvrSCaXgk7H8DexOZyjNMzXnYFg86X4Hc/aDyDOpJZGovUvn7efqT
dOwKvFBJ/TkPVSUI/q6TtN4EhtN0zTm68Qpoui7I2U2X/Ilqz9Ndj+hRkhsm
U+PvqZlc8KUIfi2H36uZbzXobz38Ww9I/NOA/jGg/zQy/2nB/22D/zWC/7TB
703MjB6NVhEYgakAGfNxeyEyFdMm8rItwd2ViDuuauYaaroNTGslaiRIFtFN
JbhNh7qb8aAJE42bHhPMjHOtEJ8nxZOjoqE+QacRN9fjhmpUVwnqqkCDDjbq
QasBmloZUyswtYHudjjQS6wpf2xENDYs6e3it7fAjlaSIQrHRy1mZmRcy9IX
q0+fpNMT5tPjom8zIlOT/M8/3bxCQjQxwYHRwQHcnkygf3gEZz5DQ71DOPPp
E8yFd0CQpybQU0MA1Lj7atzUhEGNi48f38madbZhXGxYF2JEbfiuKqGbnbmn
k8THRaJ2tfBzs/Bz5Rrt/Z1l/i6yADcp+cTLfv5PqiNnZUfOW128qXj51jYn
z6m4wq6sxqa8WlZeZVFRbV6tldTWS+sNMoNB2tBgodeJ9bWCulrWUM9vMQhb
G4XN9WyzTtBUQ6SQ7qhnjTWsoRBWptHFL0DFW6Yum24pBx01uLWCbiml2kpQ
K2GwDBIAO8rp/z1grQJ21eCuathdDrryYMd7YHoHjWmgLYVqTQPNqWSlG5NB
fRJVE0+/+4OXsIF+tJZ6tRu8Pw4/XgR5l6isM7zkA1TCdkKf2dl5Zici6PjN
MGEzvLscn51Dn4+m3u4m9o86swgcVMPEQ6j1neDuNv7LbfjmD7xnm+msQ+hi
GPrTjS65zBZfg3d/YY+G0Rd/QrFbRRdXmMf/7nB4icSXD8/M57VeFQ6ky/Yu
ENkjylUG9i1W1ieF1D319bEBcxzpnzS0pZmZwMxsqRt3HfDjbaK4PVZZV5yD
HPlKxNsUJsg9Kex/IXl7TOQggXZCvp2ADrGlPSRg91xRyh5+3hnpXBf+syMq
Q5LbqXUqDytoY045CpEja6ZR0C4WtI+EN8+Gnq/iLfaAL09Lsv5ia84J9DeY
Db4gxAI+WQMGnlkYn1peXgRTDuGJUuFkPm6OY9+soxJXwIozoO0Jzj8CXi2j
CvbCqhN09SFQfQRoz8EXW8DRaPIvyU7m4ol01HaPzv8NVhykdadhzQW69gbJ
GSnjPbr9Ad0RR5ni6K5n9MBbOJYJpvKpz2XoSxX4qgN/1+G/69HfDehvA/pm
QN+b4P+0wv+2of+a4H874X9M+O92PGUAAxW0qYAkHai9gCEuqK2Qbi1AbWXA
pKN6m7gxTQNc9TVjqkf1ZbC2iFdfSrVquUv0hnrQSC8aH8ATI3hqQjQ9JZ2c
kA72CTvaWEMtrK0C2nISUF+FmupRWyPbYiCQwlYDp319PczwkHigX9jTxfZ0
McPD5uSPEwC/fVN8+ar8NKP6NK2YGZVMjEpnBuwe3HRRh4f6Rgf6R0cFhM8j
LtQ3JIzQ5xkcRITPO4gAGOjlH+ilCfTw9feYBfD/MOjLd1CwzirGWcU6Kxln
wqCtuZujuYezxJsw6CbxdbdQkwdHC19Hma+TpdreUu0k9LAPnqM6fNzq2Dnr
uGf2mXk2xZU2FdXyKq2iptZaV6esbVDUNSh0BpmuXlKrE+pr2DqdsKFWyM3v
1XPRoOO2Rptr+M0kPSzEFek49wnIeQwKXoKqD9BQhlurUGsFMhSBxkLYWASI
8TBWwo4qNDtOGXKjCbTEtTK9NbCrjDblws5M1JVJMKQ73sP297DtHTBmgLb3
oCkF1j5j0w5Qb3dRmUdB+S1cGw/r4nnaWKqSuySUyjlNJe/nPdnIu72cd2Ux
7/E2dGouOBpKXVpI318N036jMw+g20vpk9HUrZ/QnVXo+U7u6rS4ZfTDteB8
NDyihvu8edeXwMYUp/p3Lhd+YE4EUZVXQddDybd8zYt9Ei+GXm5PP1uFn24X
hMopmZmZtznMOGQ78pL9UuR44GexLZ9na87+FKywl0B7Ea1RUVvDFPVx9lN5
ji8Oiu34tDWmfw0C9zczW8PNEw5pcu54zPMUeCuhhKFEZmZBSnqhK2+tv0h7
VTie4aB9Ql6R9IYIxatTtvsWy0Ncgbslb7VGuHOu5boY5cHF/OkSqfae1YkI
6mAYvdgeLpBTl5egzN/R2828o/7gYBR4f8o8aTtzxpdOWEW/WU2/Xs4jGe6b
Dey7HVTRAUp/HrU/5Pom2u7QfU9g41228DAoP8kbeSuYeIcLD1JZ+1D2Hir/
IKg8RzXcozufg8EUOJwORtPRQDLsfkV3vaB7X9HD6XDiI5wuAZ+r4Dc9+t4A
vzXBb834ewv+3oa+teFvRvytA/9tQv/pwv/pZv7HhL604sEaLv1vKYBNRbCp
kG4sBIYi2FKCTDVc/tLbDIc6mZE+pq+DaTfgxhrQUMFFi47kgAx3t2wXHiae
s18wNW4+NWkxPi7p7xEbm9gGHdaVg5oyoK2AdTWosZ5p0ON6LSKQtjYSccQ9
XYLBfvHomOXUpOWnGcsvX2Xfv8u/frf+8ln5eVo5MyWdmlR+nrF9cNshOFjj
GRrmHxWsDg/zCQ3xCQjxCgr0DAyYZTCIAOjpF0AA9PANclf7u/4fBlkHa9bR
hnVQ8Z1UfGcbgYut0MVe5O4k9nQy93Yx93Ix93Yw97YjIfG2t/Sws3S3F7ra
uYfaHPhLcu22bdI769wCWVmldaXWqkInrdbLaupkNbWSaq15tc5iNh80r9WK
aquFdTVifZWoqohfmo1LMmBxGsp7jTKfgIx4KjuBKnhDl2dAXSFurMRNlUxj
CSYANpWA5jLUVsGdw7b/O52gEpB/8E496qrF3dW4qwR25XI3hnTloM5sQMKU
A9qz6M4saMpCrWlU0xtQcZutuImaElDHW2B8Q7W8pJoT6LqHQPeA0t7nlV+n
8s9S6YeoJ5t4t1bwrq2g7q0Fib+B19upp2vou4t5txbRcT+D51tB4WWYcQQ+
3QQTt+DU3eDiErTJwWyfB3VlLnzzO66IYyofiG8tZW8uwdcXwJQ1oDdemnLE
IlpCB1maxdiACGu80kd4Yq105zzxLm8q6w9UddVyTaggUI5fHHQeyPf5Y5nY
CvMkmJrrIUndw9ddx+fWm8/3snSWAiVDuUl52+aYm57afynSZFxzUSvx7z/L
D65387Xm2wh5C93ZR2v5RUeZR78JvEXw5lZ5c6xFyzOnnVEiLws67U9R/ytb
/RObv+bixAMo97z4zFLRziAmypq32Jpa7UCf/xEl/YZuLMHL7HjLXamrC2DW
HqS7BrN3UFlbeWkbQMomqL2Mi/aB5tt4Mhe2PYLGeNT/ih58i+uu0fpLdPsj
ujcRmZ7Ajmd0YxyqvA6KL4LCc3TROUp7hzY+pwZTwWQeni5GU0WA0DeSCQbT
6MF0MPIBTuTB6TL4RQe/NaDvzeh7K/xuZL62MV+N+Gs7/GZC37uYf7rx/3Tj
7x1ophWNGsh/PWouBvX5oC4P6j+C2lxoKGKayFelCnY2ICKIQyZCHIGR7Wpm
OhqYtlrI7czoEVcP04K721B/Jx4f5E+NSybHLEaGJH3dkvYWUWMd0lXSNeVI
X83Ua0mgOh3S16A6LST62N8rmpyQz3ySf/ls+Z2bayH79p3rnf80I/88rfoy
bfvtk23me9Xqte4EN9/wYN/QQK8gf88AP88Afy//YC9NiJcm6F8GPX0DPdQc
hm5cPuiL7ZSM/SyDjnYiZ3sSQmc7kYuDyNVB7OpIwtzd3py4Uzc7sZtK5Goj
dXQQuVhZutnsO6RISpZn51sXlVmVVVpWaC2qay1r9JZavYWulsifpbZaXFUu
rCgSFmXz89L4Ga+Y5Hj44jb9/DqdeIdKeUBlPKM+JqGCNFiWDSryqNpSprma
31AC64oIg0xTKWitBO3V2DhLX3slaiMA6oj8cbcJdFehziLQnUf3FtA9+XRX
LtVN1jxg/AiNOciYCVrSqfZ3oPsD7svh+mJ6Mumud7QpmWpPotpeAeNL2via
g1H/AJTfpPIu8lKP8V7+wXu8nfdgA48Ql7qbfv4r83A9erSaujOfl3cOZ15i
jy7jH5vHfvgTlZ6nH27lb3eEJ8NA2S3WmETpH+LkA+yrHejjaXQqCuzzpO4u
Bzt90A9KOF9JL1bRazwEuSccJtJVzS/UkRa8RfY4UoGtzehL6yyab7EzH5yz
rrlYM2a2GP7/LL11dBTZFvbddbSqujuGu+sAMwyM3HGGgTFsgMFdggRJAoQI
IUrc3d3dPR1Pxz3ptEXRmbn+vt/f3ynuu9ZetSqVpJFTv/M8+8g+SoQ/XYwu
7MY+l5cNpm6Nt16yXg4XyMGFT2jhA6ZBimfHyNUvFw7HrH1X/Vnusw2bTeEi
EW7iuV/Xw7+tglsXCI4HafJpmHAentyK/rYYJZ3DjY6kzRXe2I1/241dfidt
brjVQ3l5O/xtLXr2PSp9hBrd+MDfwMXt3K1PYLED7PKFtTYo8yTIvwyyL3G1
DmQ4ilbexa0uWJeGVQ5oLIYa0mCHOx4KhbpEOhiMurzgcDiaSGS4YX021hbC
iSLamYwq/EHJM1jlAjpDuLE0OlXKv66nf7Tzf7WJbxuFmTI4mcdNZCNtPpqu
QPON+HU7ftON3w2QN314vhu/7KZvBxmGwtsx8e0Y/24MvRsnb8eE6V483kr6
a3l1NWktQU0FSJWPVQWkpQR1VpGuOtzThIe78OTw+5rbGqoZ40cHhH610N1G
Opuguhn2teMxZmJHRd2EYNAqZowWUwYL7YT5YJ9JZ5vQ3EDqq3FDLa9q4JtV
fEsTZWZ1qE/Qa5Wv5sz/eLP4j3eLpdoyUmUnafv83NSiuZdL/vnXiinN4qdP
1m7etfuDPZ9u+WzH9o/e6+DHe7bv3ruNxUfvU8JdeyQM/9+YzE66fBm/crm4
apVi7VrFehZr3pO4ykSK1SZME9evUKxdxkK+dpnJeguztYuElUvXbDP3C12Z
nrk0M9s8v8CisNi8uMSsuNC0KE+enyVkJwlpkQIjLsEfx75AEe4w1A2Fu4Pw
F7KEIJAdh/KSucJ0rjQLlOeg6kLaUC621inaauQt5aS1lLSVk85q9L9a9331
sL8B9zWQARUabqMjbVTaTMESwwo4WiFtpR8th8Pl0jJ75kj7CmhPDunJhCP5
aLJMMFRRfQXUlUFNMRwvwCOZeCgVD0tVK9FoBu5PRB1RoDGYqw8AlT6yYg8u
ywlEWsoYg95HOasv0fEPld7nliSeIUE/Evt9ijNfyH/ahR1+wLFnYfJVFHIa
P/8eeP2Eo86TmHPU7yBJucXXeOLOUD7xhnBlE7i8DbofVuQ/X+p9Qul/ng+9
rahyMe10EfvCtu5fh1fzsr9tEDwumg8UL+mKMsuzoke3iCe/WZbweNknq6Ap
ke3bLFQ/lesTV0zmrrp0gFjI4Aoe/7wF2X5JvlyGvE4tbXkmGBMXZlkv2Mij
ox9aXDlgsXsx3mQm22DKfaDkTn/AJzwRzu0m20zgtR0o+yEsscG3v8A/b0cP
vyENdrDaDrG/5PUPYNoFWdkNLu8SDfoRBx0n+Y+F2qe43h6lHEGZp2n+dVj2
ELS6oW5fVH4XF1yDdU9QuwunicajEWAkhIyGQE0kVruDvgCg9pP1BOGxBKzN
IJPZ1FAG51R0VsVrKlBHKq32QVVuXFswGstA0zXkdSv+q4f8s4//e5fwSkWm
KshkAdSXkKlqOttAXrZTJoXMjr7uw7OdwrSazvSQOQbmKP9ugv6hIez6cojq
OtBII+6vJ901qLMSNRfBhjxQlwvq8mFjAVQVwLZKpoB0rFfUDYtS6ftxoh0X
JobF4T55T7ugboFdrahPTUf6Bc0Iz76lm1QYjeYGg7lGs3Cg37ytRd5Yh2ur
UX2N0NIs7+qUD/WLE6Nyo8H85fySP94tZ7khM6V//LHy7bsVcy8XvZ5d9ee7
pa/n1ri7rN/+4Y4tH32y9eO9W/d8vG33bpYPbv9YYlCKDz/ZuouRyHTwww07
PiTLlvLLV4ir1sjXrFOuW2+yfr1y3RrlulXytQy9Fcq1K+RrlgmrlvArF9Hl
i+TLF4lrzKjFkmMnF73wNXl4h9regk5W0NmGc3sM3Gw5dxvO01bm9UgWYM8F
PgchnlykP4gJQvFhKDkKZiTA3GRUmIaLM1BJNi3P5WuLBVWV2FKraK2UN5VS
icEKrK4jLKHubmA6SPob5X0qob+NDHdgpoBjzXS0Bo5UorEqKu3kLcdDlSbD
lRY9hbArF6pzYF8u0JaT2QY8Uw+NtUhfiSdL8HghHMuB47lQkwvHs/BIOu6N
h60RoCkc1IfD6iBQ4c8Ve3G5ziD+nizgPD62Da1V4B1m2PlnPuc6vP8tvvej
si2Qb3DlI36Hbt/AwKMk6QYOOgTdvgfPvsWPPobWH6CkqyT1GmZSGHiCv7FR
dnMrl3lZGAs1K7fjoy/irCfKmcbVKfcX2H6n2E7B6Y8UKjfzBr+F6giT2Fum
H5mBs5/QjuB188UbPM7JTWTcJjPk+qugckJVz82+X0cfnVrvcnbBKsqtE9Ea
BXdwI7HfD+POiTe+5n/aoih9trDe2/zpSZO1JujTVfjG9wse/kzmq0wbAhUf
LuQ+NyVeR4nXD+DuXnp8K/L4EVVa48SL6MQK7tFHpNwSdzijBjuUfBJnXaC1
j0nNfT79NKmw5ifTyWAMVj3DFXdgsxNud8NtbpDFSCjSRaPRMDCfTl5moW5P
UHOfa36GugNRTwjzomAwHmlziC4P6cvQdD2ea6Jv1LyuCfcXkeZYVBsA2iLw
WB6eVeF3avrPAfKvEfSvEcrup2qlPlNfDmca8HwzedVB3/bwbwbpqwF+rps3
thN9G5mSFpHyTArfk4jn+oRRac8R7qnhexuoupa0VZGmElyXi6szcGU6LE8D
lVmwqYJ0NtIe1o33UQm3CZHF2Kg4PCjv6xZ62klfBxno4YcH6NgwPzmm0E4q
9XoLrW7R+JhZf5+yvVWsq+cb64W2FrGvVzE2ajY5aT4zvfDV66WMvtdvl795
u+wto+/VspfzS1+9XvbH25VJcSv37N2ybseerXuYF/1w657dO/4fg3u3MzZ3
7dmyc/fmnR9t/OAjsmwFv3KVuHq9uHajfP06xftQrlurWLNKvnqFfNUyccVS
ftliunQBv9RCWLIQLzHduNX03l3hykXZQ0vgbM152su8nsm8peD8XLhQHxAV
BGJDQGIkToqhybEkNZamJ9KcNJqXTvIz+KIsviSblOXxNSVKVaWiqZJXlfEN
xaSplG+tJFI+2Ih7G0hPA+pW8b0tCwc7zEY6mP+Uzr1iCjhSiaUTlyqkmfqB
cqzOF9XZJuocMFpG9HV0ppGwlp1pIFO1eKqW6sqlSunj+UhTiDUFEoYDaagr
UZo0bI1DTdGwIUwyS8U+IM+Dy3jK5TqipniLSIfFh3dS95Mk5hTMtcWRVmZn
PuafHhR9flcmXJOn3SQxv3OJF1DKLZJkhYeKNhS7LYu9SCJPIO+fsLS05gR0
PkCsdsKwI7j5Oap2oC6H6YXP+IgrvMsh4dB6tMcMnt5A1S6C4xHh7G76zVK0
lJNd/JCvecCPR1kEX5fvWSn/2zpxo5w7vYt1COTet+Z9YSt1aYs9LwhbFsAN
ZtxyBDcr4MeLuG2m0OagmHgaF90hKff4TyyQ0yFFe6B55CVl+DWxwsPkt63w
9mfY/Sjv9DW6swsnPxDiz/JpV7DHj/DiKuj8CSq0JG3OeK5IbPEkySdJ1VPU
6U/y7tGwQ0SfLe8JoMXXQcNT0OoMe73xUCDWxKHxGDLiCybCULWjWO1o0eSu
qH5MuqNoVxDt8MW9kag7HHRFwZF0oivCU5XEWMm6RDLfSqUCaD2CppH05sO2
RNCZCFkKP9tE3vXQf46Sf09QFv8YJa+7iVGF9HXI2CBVj3nZTRiGrwfpfK+0
ucnQQbWtRMdg7CbzQ+SdhjJNnOqhfTW4uRCoilFzGW6vIR11pKWaNJdjponl
GbAwGRQmwaIUVJXH1xXRpiqsbqaD3cLIoDg6LIyOCCND4mC/MNAnDPSKzHMO
9dPhQX58VKmZMNFNmuu0iyYmFw4OLmpvM2tulre3m/T2WoyMLtLrFs3OLp17
ufTlq+Wv3zAYV756s/Ll65WvXq3+849VzXUbDh/ZsvaDHdLIzN7t21hiuGv3
+9xwzzaJQWZHd29iDC5fIaxeLV+7Qb5+i3L9JpMN65Us1q1Vrl0lrlomLF9M
ly2kSy34JeZ0iZm42IKYm39zUPHoPnCyRT6uXJAPF+LHBfvKQny5IG9ZdChM
jMFJsSg1kSbF0YRYeXKCPDNVzMkQcjNIYbZQmC0vyBZK8/jKYkVDmWlDiVhf
guuLkaqSttULnQ28uoGw3qxb2ljB97WL/e3icCseaUKDVWSwErMYqEB9Zbi3
TFos0ZYN1FlkoJAaVZC5l5dS1Ts800yMDVRfzQDkNUVYV4K0JXiiCI4VoIFM
1JXCqdNxRzppSgANkbAmAJb6gEJPLseJS7PhClz4P9UWE0ULsp+T5Dso4jzs
yVSOFi8+8RkvDfVb0Mgr5hmWyP8gCD+O/E9Qn1O8OsLc4Qj/8Dsh9prc/yh4
/iWMvcxlPuJd95PUB6QjhGbcx2d3kU+Wkktb2GdCRsqV3eTUesRA2L8B7l4A
dirg1+sEhs+xDdD2a3phK6303FTrvu7rZXCJwK2Sc/f3mZffRSP+8vjrii3M
ai7EVgeVf1uCVlngzQvAF0vhjZ3Y5zC6+yliiWfY73zHYxp8kn61HBzbih99
Sxqe8xNZYtlz3vsAKr1Ls67SGhex0l2ebs1nWvExx0DxbVL2gGZdJDlXcL0L
P5zIVznzLh9xsUdo/ROx3BKUW6O4izTrBi6+wTfZkG4v1OsKRwLg/U/QNxbg
wGrw6ABujRX+1WvaF44aXUFfDO6PI90xXH8ynMzHM5XSZiV9DZ1pIvOd+HUv
ejVEptX8SJW0qL4nQyqaPdWE/xrB/9KRf+v4/06R/xiEt0PY0Aw0NViv4mfU
5OUAeT3Ezw/iuQE63UP1HXiymWiaqLYdzbOEUUf/1Iu6Dr65AFSlwrJkWJkF
6gpwYwlpKsdMBOtLSWUuKkqF+cyMxUmRn4iK01BVPmmsIp1M3bqVg4y7IWF4
SDk8yHikg/08g3G4n+HJxJHppqlxaqFxerlGu7JvYEFHp0lbu7K3z2x0bKHe
sHx6evns3Ir5l6tfvl798tXqV6/WvHyz+u//XN3TufmHA5vX7ti1dfeHW3Z/
vPWjj7Z+uJu5UGl0dNdHm3fs2rh9J16xQlizWli3UdywzWTDVtMNG5VMChmA
q1ewvE9Ytoh/DyC/xJRfohQXm2Iz08+/Ju4uJMgXhQXAiCAUHgTDA7mQABAZ
AZPjKYuUJCExXkiI5ZOThKwMOQMwJ53Pyxbyc+T52fKifLG2VFlbKtaW8PWl
fEM5aaom7Y2KDgZg/XsdVIk97YqBDvlAO+1vwdLesUppgr6vAveU4q5i1Mno
yyUt6aC/BOub8EwHmW0X5zvoXBuZbkbGRqKrIZMVcLIc6SvI+2X5aOx9DaiB
fDBYgPtyiTodtSWAxnBph2+FHyhylxW7cplPYMoj3BDJF7rimNs46DqOtVPW
RZuVeYtHt/H713BWX+PQk5BZUN+DMPAEPbuJXNmOLu1Fny2X/bpeme+4LM0S
vthPQk9Tn1/hvQ/A3e0w4hyJuADvfSZc/hjafoUTz8E6Vy7+Irn/FW+7FxzZ
gm1/5JNvy1W+ixwO80sh2MhDpyOK8eQlxuJF/peFdTxcy8P1VHZ5Bw49g698
TjZjmfOxxb1Ri5LumX25Au8w53aYgl1m4KuF4GNz7ouF3NkNMPgA8jjA/W05
+nELiD4Ly6/jdndU8pBEnydFNnyVI+0JFTTpWB1NXjUvavAyTbsECm6ROkfU
6AKjf4FV1rTACnntBcmnSJMjbHoEE8+T39bAUEuFpsKs9pnY/4LOJCBDEt/q
IoZdFi7v5m2/JXX+aL6GH4wk1Xag2ZMbiAKjabg/GfUmgpH0/yV6WF+Jphro
TKsw207m+9DrEZblCSO1tLcI9hWB8Sr4sof+Q0v/aaD/nkL/d578d0Z8PUQn
G9FEHdK3sB+m80P05bBUNGZ6kBp7iL6Ln2il2hbe0Mk0Eb3T8vPD/LAKtZag
qkxQmoxKkmBJMijPBNX5qL4E1ZXgqkJYnguL01F+EsqNx9kxMDMG5CSi0lyh
rkJsbuTVHUJfjzg4IB8cUAwPmgwPKQYH+KFBcaifsakcH2Me1Xx6Zolxao1m
cs3Q0NL+/sVDw0vGJpboDSumZ1bPza2ef7ny1fyauVcbX75a9/bPTR0dmw7+
vHXdNobhri27pfoVDMDN0vzgrk0f7NywfQdZuVJYs0ZYt16xgYngJuX69Yp1
a+VrVgmrl/Mrl/DLFtFl5mSZmbjITFhighdaWCw1u2olDwsVwoJIZBCKCoFR
4TA8FERFkYREPjlBTEs0SYgWY6KF1BTTjAxFVoaQnS7kZSpyWeQoC/OVlaUm
NSXymmK+phjXl/GqGnlrvdBax3c0iJ31ggRgh6K3Xd7fwvfWo64K0MvQqyRd
5Qw91F5I2vJxaxZS52NNoyjVteui82oyr8asWaebpJUVUiWuatbrImMtNlRL
22E0LH+sRCNlaKwMDRWhoXzcl4k7EkBrLFJFwLogrtYfVHhLZWeSHqCI6yDu
Lgg+D/yPcpGWpmG2ovtZ8ekvOOaCWGgHo88Ql29Q2GGO5YN3dsKHe/H9T8Dj
/dTvLCl4jBPO4sgz6MVP+MY6cGcbuLEV3FiPvH7kfQ6ix18T273I7weYc4/m
2MCLW8GtnSTwDI07RVU2aNifFD+mH5vgbQIOPCs0h/GTeUvS7sHbX+BDG4Ur
XwtbBfSZKdq+AO5bjTJuyvu85C0eisNb0A9riftvJt+vBB+Zgs+XwE/Mwb5F
yPswDPgV/rQeHNoGcm7hwP0gYB9y3A0ebuNyH5LuSBj3G0m7IhQ/RapQk7bo
xXGnYPFdVGmLkn5DkQdB6D4Yd4wGfg+L7pMuL6R2hd3+QvjvJOU+fquWT2aK
w0HozzI8HkVarcFYAB4Jx62e/EgcmUxGI9G4yUWKVk/UGyEVmRzJRP1JSBLE
AjxdQw2sUergtApPNUtt92oEvxwl0z3CWANhDmeoAuta6Oth/M8p4d9z9L/z
6P97Rf89Teb6kLaFTKiwrh1P9aC5UfJqXJgb4WeHqLGX6tRIq5Z2eRt66csx
/GqCTA2R4VbSWo4bimBFBi5IJPnxuCAJFGdwDMDKAlRdRCrzUVkOewILU1FO
AsqMgyxyU1BJDq0tE1V1fGszUauFnh6R5YNDg2Yjw8rhIZOhAeXokEIzajI5
YWHQL52eXms0btBoVo5PsFih0a5gmjg1vXhmZtns3Mr52XVz82v/+Gtzt3rz
L4c3rv5g1+aPd27+kMmfNCK68QMWO9czBlcsExhxa9fIGXqSAkqZoLBqhbBq
GS8Z0QVkqTlZohSWmKLFykWrF1pZK0PCTEKCSWgIiQzHMVEkKgrHMNVLViQl
KBJj5NEhJCaCT04xSctQpqWJGWliZrqQnaHIzVYU5puWFphWFZtWFgrVxbyq
2qSxVq6qF9saTJrr5B1NZuoWk+5WsaeF76onnRWwk6V7ZaSzBLWX4OYC2JQL
WnJhdwlrC5YX8PN9ZK6HzPTg2S6pyKSxSaqAZ2hgTfy+SnMDnm6ghjqibUAT
tXCynoxXYcbgWAkZYaY0C/amIXUi7IiDHTGoKQzUBYNKX1jgBrIdZSkPuYir
IPwicP5NeWiH/N6Pix5/jVy+wqm3SfBJ4vodCv6FZN3FbvuQ+34Qd4l0RfDq
KJJvR2LP8Lk2OPsJufchuL+Ts90BfX8ilZ405Q72+ZUk30KFDjD4uOD8FbX9
ilxeK3P9Dnsc4J2/JL5fQ7svyA4C9i+Dzj/T+1/y1j8Quy9RgTWtcpIPhIt3
v0ZbRXjuMxz5QEx8IAxlmiZbkuCzJOuWfCBkWeytJfuX4m8XgXv7Raka1efY
7Uf0+FvifJiPOS34/4gjTyGXfcRmJ3zxFSx6iEIPgYADMOE09P2F+BwTcu7g
0nsk+DsQvA/FHgX5N6jKkaRcJLnXaO1T0vAEd7uB8SjcF07GEki/H9LEotlC
UmUL8i9zTU/hgA/UhIHJaDAZj3UpUJOIh6Nppx/q8EO9UWgkFWny+LEcMpAK
R3KRpgRP10klQ6V+sh7NtPNzvfj1CHw9zmjiR1VI2ixfjw3dUpnQf0yT/7zC
/31F//uG/Ocl/2qcTrTiMRXWtJCpXjw3wojjX2nIzBDR92Idk0UWfdQ4IBUz
nBvlR9tIWzFuKuYbSnB1Pi3N4PMScEYUyoxCuQm4MIWUZKCSTFSSjUqz2RUW
pMGcZJwZj7ISUF4aKcykJbl8ZYmivkbRpBI724SeLmV/j2KgVzE0YDrYZzLY
pxwZUk5MmOn1iw36FUbjRuPUVqNxs8G4XqdbadAvm55eMTOzdnpmzdvXm3ST
m69abli1Ybs0DrNrx/sJemliYt22D/CKpe/nB1cLa9cKa1eLq1eKq1bwK5bR
5dI4DFlqRhYrxIVyuGQRv8j8wjVleLgQEqQMCRGCQ0hYhBARxccnyhPi5Qmx
ioQoeXgQjgyjySnKlFRFSrKQnipPTxUyM+TZWSZ52cqSPNOyXEV5rrya/buq
FA2MwTq5qkForle2Nll0NJupm+TqRtpWCdtKQEcZYei1FKGWAtKYDRuyYHsR
GmnAUiYu1ayjM71YOoROqvBD9K1I34wNTcigkuohGBulbtagIjrWXiqkbSIT
1VBThTSVZKwEjRXCUaksMBzIgIOZpDvx/S6nWNgYIe2vL3Fh2RyXcAPFX+ed
T8uv7OWv7sC2X0DnLyQjmnsXxx3j3L/gIo6h1Kt87GlQ9JjWvEAplsT3Z5B+
h4+7JKRaoeffwaefQ+sdIPU27c/mY24jyy34yafE/yj1PiSPv02zHMSoGybO
+7DfYZx4T352Pfx1GbLaj91O8E9/wN8ul32+Cl3aQUN/JbX30EQoTbst7lSA
W3vE9iha4IZmas1qfeQZl3HRbVRrj0uemJ9ZT298QkoeLeryNmVm2P5vJOwk
znuIfQ7gtPOw1JZ4foOf7kSxJ1DxPT7uFCiy5lWeMP8+LbQm7Z64wZW67wVM
+5ggVlnhOiuUcxW3u5Eeb779ORz0QcOBaCxAwq3LAw+Hc5OpUB2IC+/ivOuc
yhEMBsDxKDgRC7SJUJ8CtMmMRDoURfojYG84N5yMJvPIeD4cykbDuYQl5lJu
2CjqqvFkFZpqYX5GmOvHr8bx/AgxDvCjLXionoy1CPpe8oZliK/Jf97i/7zD
/+dP+vd5MjNIJprxSAPUtEmFCmeHyEsNmZ/AU4NE20V03ZSp4dQAnR2hcyPy
4SaxIROXJTJHSoqTcXEKzE/is2JwahhIDUUsUtg1DGTGoexElJuM89KkYGqY
k4xymFlNYQHzM3BxgVBdIdZVy5sa5C0qoaNd3ttjNtBr1ttt0t0p7+0WB/qU
4+MLtLrlev06g3GTYfpDw/R2nXGjXr/eaFihN65+82qjbnK71Z2NKzbvXLeT
KeBHG96L4Nqt2xmDdNVyyrhbvYrByK9YTlcsJcsWk6UL8WJzutgEL1EoF1gA
C9PtH8t9fc0DA0z8AsUAfzEkhIaEiZExioQ4eXykEBNMQ/xgRAhNSjJJTBaT
ksT0ZGVasiItRZGZZpqdbpqfZVaYa1qcp6gsM6mpMK2tMm2sM2moN2+sX9Ci
MmtVydsa+NYq3FwCmktRaylpKcRNBaAhF9Zm4Pos0M9y8y6pdpZEXz8DkEjV
XHt4o1qq8mpskXRwqgVPtRJjG5GurVTXQrTNWNdMNXVIW4u11XiiAk2UYdYV
s9dgtACOF6HhHDSYiQYyYW8mao6FTaGg3h+WPAd59iDdGjrtgw/2gDsfwhdH
gN9xaLcHee1DXsdMoy4IyZdwzEku4QzOssK+P0GnL4nnDyT1Jow5R0OP8T6H
sMMX0PojLvGGotCO9/0dnV4Nrm7ibm6UWW6A5c/5+gD2Ei6o9VUkXccpN8mz
/XzQGaryQaW2+NFecHo7cjxEr25Hzl+Tgts4+jh69Dl+8CkNO0ErXEWnAyTx
gSLVBnkeoj4HcfQZ6P0jObEOuOynVQ/xoK9yPJpPuoztPkHFtrzH11zefVxm
RwMPESaI6Rdw5gWYconvjea7gkH0ERR5FHcFknZ/4v8DrHNWlt8hWZekQZhG
F34gEg0Gok5P3OLGz2XxPR6o9g5kuKlfAE0CNubR3ihc9hjm3uQancBoBJlM
5DQJjEFsSEfaFKBLhtpkPBqHBmLgYBJTQ2meaLQIDxXg4ULA2sLYSI31VFOJ
9SoypWYNKiV6rxlQGn6yj0i1TRqJpoNOj/B/zvH/eUf+/Zb+nz/4//sn/9es
aOihQ3WAKaa2nTcwOzRCX2uFuTGpltpEp1RLzTBEp8fJ9BjW9/G9NUTF/Gc6
LknAeTEoOwpmhIGUIJAUiBL8YJQ3jPSGUb4w1h8mBMGkcJgWgzLiUFYizk7C
DEbGZn4azc8iJfliebFYXS6vruRrKkgzS53azXvUZkwfu9WKLgZjl3Ko32x8
bOHk5Aqtfq3OsEWr/2hSv0drXGc0rJqf3TQzs/HR4/Ur129du30XA3Ddtu2M
QbR8MZFUb9l77VtKly0hSxfjJQvIEnO0yAQtkvPS1Vyx0OS6pdI/QOntK/j4
C4GBYnCwEBouRETyMWE4MhAFeKHQIBzPeIxTxMYKTBmTE5UpKcr0NNP0FNOs
FLO8TNP8HGVpsXl5qUllhUlNtVl9rWlDnWljvamqXtFUwzeUwcYS1FJCmoph
Yz5uKMC1uaguB7aVotEWYbqfAYinBshMH53tlzCc6iHTXdSg5o0d1NiGp9vJ
VAdhmsi+NLRLY9e693XzdMygNtL/Mchyw8ly/L86QpOlrEPGo/lkmPXP+aQ7
FbbHgvYoqAqAVZ6ySncYfRHZfQPsvwdPvuA8DyO7ffDiLnBwHTq6e3nW01VZ
t2jAL1zkES7fmpY78TXuAhOdwMPwxT4u9DeafhtFnydXNsgurcbPvyHJd/Hz
Hxhc6PHfwO1tIPmmmHyP5jnLwy+L7vuR3Wcw4jiKPkmSz6HCB8T3BL79IQ46
DB99wnkcgE+/QUcWwvNbceo5Um1NC+4Qx4P0yFb48FPycA+KOQ8LHxO/48Lv
q7i7W6DPd7DgFjJk8k2+xP8XmnMbJ58FObcFlqa1+qHkC6LbXhB7GOTfoarn
uPoJjjiKPL7EJQ9x6WPq+R1qcCW552HqWRBzHXQnCYZ8XG9Lc67xl7bDp9/x
mXcVrENQu4DhcNTlD7W5RFsAhpJJnSsssILNLnA8DurTgC4Vs+tUFjCkMUFE
+jSsTcfS0bppZCSLTJRQTYVUrWKIuZFSpK/FzLRoa5GuHklFs7vo7KAkai91
EkETPXCoBQ02oQk1nR3n/5oX//VO8e8/+P/8xf/rrXxey090kcF6NNxIxzuo
rh+xn3mp46dGyCQjsRvrB/npMelLwwAdb6fqCqJi71U+rcklVdl8SSrOiUNp
ESAxBMb4gXAvLswdhLhyIe4g1AOEeYIoXxAfBJPDcWoUykgg2akkP5MUZJFC
9rv5fFkRX5yPS/JRdRnfWMO3tirb25Sd7YrODrGzk/lVk8F+0+GBBWMjy8Yn
Nk1qtxoM65k7nZlZMz29w8Fhw6pNH6z8YMu6bbvWbmM6uIQsX0KWMfqWvqdv
IVxkjixMCIsFSrpAwS82hQvkX36n9PRWvPAkXl7U15/3DxICQxUhwXxEEA32
Qr7usqBAEhmpYE41KlLOIiZGnpCoTE42SUkxSWW5Yao8J1NRmGdWXGBeXGxW
VmJaWWFeXWVWW61sqBZqS3F9CWwoY1dUXwQbilBVAazMgm1FZLyDNw4y9JjB
YGaDzgwLMwOU5QJSneQefkpNDQxANQuJR3Z9/4RIp7J20MkWZGhm+kh0DayJ
sY4paRWvrcD6Sqwtx+PvF5qOFuOhItyTidQsMYwCTSFcvT+o8eEK7FHQUehz
iPP6iYu7xTdHLnY8Z77aHO5ayN//Xsx+JMSdhWk3YeJF/PwrEH6KCY287All
khR3Tog5jVKuoue/8Jf3iM9+ov6HMLOpLl8h/19g9AUSdR7nPiTh58VfVpPv
10Obz7nrm6D7z8hqB7ixGVrtJK7f08QHOOQ8zbTiY2/wlp+g02vx2VUw+gSu
dQGlNpzn98TtCIk4zT/djRKuE++D9M5H8MF29HAnYFTe3MT0V3D6VHyxj1Q6
CO0Mxp9QkbVY7Uzc99LwX3HYEZRlCZvccfZVHHOUFFjCopvQ/zvy/FMUclAS
tcJrOOokLHiC+sNpsx3s80GuP4kfm8DfP4Q1fhbjicJwOBmMhJ2+1FCMdcVo
Io+0hsLCBzIVwzCWzORgfSbUpnPGXGDIQZOMwVQwlYN0uWQ0E45kQ9b1aWuI
TjoxBI0U4wnWHLVU6ifr0GQ9NrbLZ/sUU4N4fhK/NtB5HZ0cIAPNqL8RjarR
1AR+Nyv/1zvlP9+J//pL/Mcf4iu9ONqGe+vZD5DhVmwYpv87PXBqVJgcgNoB
qh/m9UNENyAMNclLo3GqD0rzQ5nBMDcSFiWRknRalkULM1BWEpM/Li4YhPug
YHfo+wx423NeLBw4/+dcsAcXE4QSI3FaHMpNpQUZfEEmLsymuek4J5XmpuKC
TL44h5QX4aoKUlstb24y6+iw6Ooy7+0x7+4x6+u3GBpcPD68SqNZOj21/PX8
ZjfntavXbViyZfuq7RslBldKGOL3ADLJQwtMgKkcmojYTE7NlWSB6dJ1Fvdt
TFyd5W6u/Asv0duP9w0U/QPlQb58oCf2cJL5eJKgYDEoSIrQMDEiSh4TZ5qQ
YBIXr0hIUCYnKdMylFmZypxMk9wsk/w8k5Jii9Ji08py0+oyeWURqilCdSWw
uhBUF8GaIliZDSuycGc10fVhlh3oe0RDH50aplNDvAQje9jHT/UJ+k5sYJZD
kkJpYM3YRaa6KXuo76SGTqptQ8ZOfqqFZYVIr5KOidHXScf6GGupnpnScshe
gNEyNF5BBgpwTxrojYedkbAxUGKw2gdkPkQRx7nI01zgIa4p3OQ/gwvzfBYe
WI69zpNKR5p4iQv4BRbYwrS72O4z4PQlSL8vFHuYPDlAIm9YJJ1Gqef4iAt8
b6ppwwsh+Czv8RMJ+JXz/gZGnALO3xCvH3H0eXT/C3hxLw08ITp+AXx+Fa5t
gb+v446v4By+gW0xuMAOR54Vm0LpZOGiwNOC9V6ab8s3+ZNSZzHN0iThAk48
jwoeKXx/Rfd3ci5f8sx5Jl8h6Tep5SZ6aRN3Y5PMahsMOUIZ748+Qo+2o2xL
xHTW/QC+8iGOteInC0WVO0k5iXIvgtJ7MP4EjPiRSzmBVQ58swOusUEqR77J
GQwE8jNxaDKJf/QNsf2ODiaIfzYqVY5oIh71BnN9MWiqAmmKWZDGQFz0WNbk
DiYSwUwhms5HugxgzINThVCfhbTJQJ+FjQVMOuFoNhopkCyooZHX1KKhMjBW
Tceqka6R6lV0ooHTtZLpXvlUPzUMIgbU6xk8q+MneoW+RtLfJIx3CVPj9K83
wt/fCn9/o/jXn/I/X4r6Idyvwt3V0ppGTR82jJAZjTg7KegG6SR7YcZ4wxjR
DZMJtbwuk2SHcKlM4zxA1HMukoUrF+sNU4NJbiwukFJCmJkCkqNBTCAM9gDe
zziPJ5yrDXB/wnk7wUA3FOmHE8JgagzKTMCMx9x0kpWKMxKhpJUpQm4ayU3D
+YzQHFxZKlfVm7e3W6i7LRiMQ93mgwPyocFlWs0yg26Tl/fGz79dvWLTZrJq
MV25FC9fjJgCLjSHC0yguZJTisBEQOZybKEg5vJ9vyxwcBDs7cgzF971hfjC
z+SFrzzQm/dzwc+fyNxdgJ+v6OOr8POTBwXKQ8PlkbGKqDhlTLTI1DAuTpGU
oExJUqYmy9NSxawsZW6uMi9PXlQgL8vjy/NQRQGqyIcV+aCyEFcycc8ANXks
EaD6fn5ygOoGiHEYTw/zrH/Ts3v238se9lC9WtJBfY90b2CC2E2YNdWpMUvS
dZIU4uluQd9ODK1YGi9VYX0j1knrLrCuFmkqoabqfVdcL4xXC/25aDADDiSh
9wf4wsYAUOUJ02+B1Ksg/gIXdBgUPBH62X+yNYq5jDKsQPxlLugQF/AzSLiC
ku4Qlx+A71FQFaDQNywKs5T7/AKLbktbpZKsyOvGhcm28q8XYu/zi6JPIe/v
OPcD9OwacGE1sP8ExV4CYWdQzHEUfAymW8HnB8i51bKL6zj7z1GWHb73MX68
G6c+4MfSTRMeii7fkaTLwPdn/uxyeG0jzLIWGgJxT7zQ4EPz7ISIkzTmuJBv
jXKtsdPn6M5mYLMDPPscJl/hw0+C2xuA98+YpXilVtDmS/jFQuBxXjSUm1Ta
4MQTHMsNy56jviR5mzdROaPRSNroQuIOgdqHWO2OurzwXCp+kwENydKm/oEY
MpxAy+6CzhdwPA23B4LhZEFfBqUaoSw/CielDrI2b6hLw3MlaLYYGrPQVB6a
LkaGPKxJlfZKTBczDPFILhwtwOOl0KAiGhUZrkTDVWSkCmpVLI/gJ1VY20KM
3YKxX9QyzzPEz+nhq2kyNS4fbCN9TdIZzeP9jE3xH2/kf3/9Pt4qXk7JRztx
VxXsqSWjHdIB9NMT0mGChlGq6aXGMXFqQs4e6gfFngZSnQOLk3FuNEoNhnE+
MOw59LXjfB9xfg4gxA3EBuCUSJyZgDJiYXIUjAuDEf7QzxV4PgWuNpybLXjx
FHg7SvoY4QVjAlFcGE2MIPFhiF2TI3EK867x5H/pZG4KLMzEZYWKhlqTzlaT
3h6zob6FQ4OK8bFFBsPK7s7NwaFrGX2EAbh0EVxkgS3MoJkpMFFAhRwqRGjK
MDQxX2F66aZo/ZC3tiVOz6ibl8LtheDmSlzsoYMNcLZHLzzpCy/ey4sxqAgK
VYRGKELCBClbDJFHRspjWXoYI4+NFBPjFGmpisxMk6wsRW62kJeBmQEozoTF
WaA0FzFfXZQJSjK4pnJpY6C2n9cOEMadcYQahyjjjoXE4IA0/iwx2CsBqH9f
XdnIMGQK2E303VSrxno1nermje8TQ2MbzzA0vJ+2MKooU0Pt+3N8jI2IeVRN
PR0tQaN5aEQqNAS7o7nOCNQSjCqegZx7IPkaF3YcMEeaYikrdeJKnECxI5f7
iEu7LWM6GHGGC/ydi7iIwk5zAb9xSVa0PZbGWfIBB2HaJRB5Fr34iaQ94J8e
Ec5/jEPPkcgTOPYkSLrB2/wN3v8IJFiSlgiUZcs7f49df8T5DjDRktzcDiy3
c48+RTafQMvtyHEf9jshOh0l5/eChx/zESew9U50eQO8vhn4/Ujaw0ixHW4P
46tcQexZ7PctjfkdZ92l5Y5Cyg0S8DOJP0eKrGD0cfx0L8qz5hufw0JLmnKR
uv4Cg86L5Y408wwKOwzv7gGZdni2RhiIJI12RJ+KWzxQ1jWYeAwUX0ctz6Eu
ARniiTEGzaXD2UI0kUFr7EHNI9gTgoaTYFsQGslAkyVEV061VbQjHtV5gJ4Q
5kXBXAlhYchhUkhmSrCxEGoljwoNechYRjQlcKIUTZQhfQPVNVDWFsPVjEQ0
Uc/rmnlDG9U2Y9aLsvaVTpPvY34SM12b0QrjvZSR2NuMB9uJdoi+mpa/m5f/
8VL4643450uFboj2NdO2KtTfjKXDPZl9mqCGMdaf85oBRqIwNcFPTwij3bSl
AlfnkMosVJBKcuJgegRICIShntDXEb54wnk+5rwdoP9zGOQOQxho/jAhHCaG
49gQFO4LmD76PQdeTzkGo4cdx+KFPfB24HycOH9nLsgVsM+J9EVxQSghHKXF
0awkmpOMirNpdZnYXK9QMxi7TIb6TSfHFxiMS9HShSwYgHCBOTA1kSmVnELO
yUWZnAdKnlMq1mwxvX4LW96EVg/J02dyR2feyQHZ23I2VrKntsiFUelG3d2p
t4/oHyAGhir9A8VAf2ngNJgljGHK4GBFYKAQHiHGM1OaqshIk2ck04wknJ2M
spNJTgoozIaFOSg3BVTk4y6VONbN6GNeghpGecOQVLFHJ50YzmwJr+1FLHR9
ZLKPsEaRSGT09QrvTxMQdF38ZLt0rIChR3KnUpLYQac6eH0LMrbR6XZBx6Sw
QXI7U214qpNqmshYBdQU48lCMpaNhlLhYDLqjueaA2GxHUi7wYUfh5G/wyJ7
rs4XVXuBKg+uwkVW4ijLtZGl3AWR17mwy1z4RVnUZS7gmCzkd/DsR+TwPRf6
O4k/jSKOAO+D0P5vIPQUbfJRVNmjQmuUcxsWPcFBv0OvH0GlM42/zd/eRb5c
in7bzJAnideh+wGpoGLoSRR4lKbeZ3YUhZxEJzaDszup73E+/hwK/o1a70CP
PgS2H8AX36PHH1GPH3CxHfX8GvgclIUdxrk3qToAqVxJwA846BhibjnnDgk7
geLPi7HHkfeXIPQX0uRA1R60zgm1u+AGB+T1M427RiYyxeLbqPgmaXNHPT5g
JBzWO+Pk81yFFRz0I9LEXxIwJkNjCpxmniEC1T1D9Q7caAIeSkZtIXA0h2pK
kbaa19bC9jjYEICHo4k2Fc2VoZeVeKqQmypGM2Voqhjqc5EmA+pykLSArRqx
9HyykmiqmBGV0BupQsOVeLyeH2tEmhaqZ63WjifbsaGXN/TxY+1QP8SYYtLG
j3XTPhXfU8f3NyPtMH05Jb6ZpW9nxT/fiK/nlKO9fGsF6KhAQ20Kxqx2mDAd
1I8I+lHpvdKPEaNGmBiS1xSgwnhYlCYrSQFFaaAwDeQngcxomBjMCALBnpyX
E3Czk7TP5T7nYi2ZUr9nINQDRvqR6EAUHQgjAziGZJAn8HNhmSP0eAKfWwPH
e9zTO5z9bZnDLc75HuduywU8gxEv2MfiDGZ3U2lFLq0tF+qrhaZGQa024Rh6
C8yhuaSAnNJEplDKGICiIBN5TsFDE8WiVcpTZ/kbN7CVjWj7VLSxgbb3OZt7
3JNH4JkjcnUjHp6Cu6fo5aPwDVB4+wnevqKvj+gXoAwIUvr5iN4eNCBQiIrl
E5LFlFQhJYEkR6OkGJgSD7LSuLxM5qhRQRpoqhL6O+VjvVg3RCTDMISlPHqQ
SvUhhyUAJ3uwlnWJ/bxGOkOc8Uh1rF16eU0X1vUwDCkD0MD8p5rqGICd0gDp
NDOl7Qw3MtVOtU1I1ywVyZd2wXRTXRthCchk+fvjJovQaCYYTkXDaag7Dta4
g8w7IPoUl3COYxKjCgB13lAC0JUrewbybKV999E3ZGE3QdhVEHmZCz7NeR/j
XA5B34uC9ff0p7XE+hsh/RoffJDz3U8Sz/M1rswQkgIbEn4ceH4Dw4+j9Jso
4DT8aiH3oRnYagFObAIZt3m/X8GL76HzVzDoN/TkU+z5C466jOIvkOAjyPdX
EnsGZV3F5XY48Tp6/DGw3QPcvkMRF0mWrUnyDRRyGrbEKptDhIIHXMsLmn2b
PtnOBZ6BJd5IW0Z7YmjuXRL2Cxf+M4g9BKN/RXFHYervoNOHGFOxLp7v9KJd
XqjPF6ndYYsTGvTHhlTABKvBE2ZdIrV2YDyWm84CxixuOpubz8RTqWg0Tiqs
2u5DxjNRbzJQRwNNCdaUCtoqPFlN1UxMg7i+CKjLBvMV+E0tmS4FzJHOVhBj
KdTmY00GmcwCMxVoRkrSsa6aaOuoToUNbYJGRUdq0XAt31+JB2uwplnatKtp
lU5KMg4KI61kpA3rBkX9MBNBMqLmexqxuh4NtElu86WRvjTyb2blf742N06Y
dNXQ5hLYWYtHuuh4rySahjFBNyrXjyu07GZMrh2Sl6aLXs9W+LisCfZYEuJp
Fu4tRPqDqEBZlL8sylcW4SsL85aFvpD5u8u8nss8nDhXO86ZIWnDuT+WwvMp
SxI5H2fg+5xjZtXXBXo/g54O8LkN52Ale3JD9uia7PF1zu66zP667Nldmedj
GOwC4wMBc6r5GaSskNRWCzIzE870fZgw+pQyUS7jeSkECuSUKOXETL73E/Hq
TeH2A3rnDrh/R3b/puyhFbB3pM+ceRdX0cWFXXk3D8HNjXdzJ+4ezJoqPL3k
7u68x3Pk78OHhctjYuVxMUIs88wRKCESJcWSzDSSlU4yklBxFupQ8SPd/MQg
0Y4QLeOuX9I+pobsqh8W2I22l0g1Q/qopIADdJLZUXbfSzTSjYQhk0KWCWo7
sbaT6DrpFLOjjMQOJA2WdlJdC9K3SdZ0tleaWDSqmQvFuipsKCeGSl5bCMcz
0HgWYZ6qPZzZNi72NEi+DJu8UHMAaPRHdd5cjTRbwRU5cRkPuITbXNQdLtIK
RN/hYm5ywWdk3sc5v9OwK0lZ4Gnx+SJq/aM82RKGHyOpl2DkMZx8jU+/RRIu
QddvoN8vIOYUTLkOf9uCF5tiln9/tRo67edjLwvu+6H/L9DxS+h6EJ3fiE4s
5VjeF3CEVDihrPs44RKNOkdzrVmKCt2+wb4HYPpV0hmGu8Nw6jWQ+UB6/1/X
8h0+qMMPJp0FwT9j70MwwYr0xvDGfJRniYK/g0nHQMZpkHeNy7iE4o7Bajs6
nY+n03CvF+p2BcP+UBuJDQlM75AxE7wsIuwXVb4o7y7X6QGnMvB8CZ4qACzm
ivF0NtKl4p4g0BOGJnJpdzzsSyJ6lmiXEX0tnWoivZm4IxSPxiP2IfOV8E2D
MF2MjSVwugpNVWBdAdRm4cksZJSWzfD6WsxyBD1LGVqRoYM1kDDeiAeqcXc5
6SiA/RVkvEkYb8XaHmIcpppuoV+FpUPSewXdMD8xQHtbUEcNUteQEdbxauic
lszr6Nt55atpfrSLNJWAlnLc3yaMdEvb5yfZJ7DufUzUSiSKjMqUtL3H7z86
dNfpt3t3f79z89Tda+funbny8NBNm4NWj7+0ffqpg/1OR/s1z+0sXJ7KXe2R
u73Mw0HmaS/ztpf5OMp8nsm8naTwcpK9cJK+5eHAFBO42AAHK+6xJff4puyJ
Jff0Fnh6i3t6k7O/yT27I/O04QIcQbgHSAwlLPuTmcplJqJMIUoM8nIZFTkq
yHgKBB7LBd5UqVwo//xb4co1dO0SvH4J3rgCrO5hW1tq+4jaWEM7O+LowNs/
Jfb2xMmROj0TnJ7xjnbI5Tnv6yeGhMnDw+XhwSQsEEeF4DiWsSYK6al8aiLK
T8f1VbS3k47204l+Mt5HNMy0D5LJfsTkjzl5xiN7Mjko6AaESaaA/UTD7Gi/
BKmmlzlSlmsTjXQaBdV1UUkKOwlj0CC5UDzTLRVIn+pifoaf6sDTXWSmX5jq
Y5kj0aqkaSlpQWkN0VUQaVtTPtTkoeF0WuwA48/B7NuozQ+pQ2BLCFAFwkY/
Kep9QLkbyHfi0p9yKQ4g9SmX48hlPuaS7nExt2QRliDPkZS7CX5n+KSrJPAo
dPmWZFui7Huo6DEtekITL+Pk23zWHZp4Dj/Yjxe/HwA7sAVFX6cNvqTcl6rC
5NkPePdvQeARmHCTeBwhVrtAzCWijgGlz9Hjz/C51SD5Jk2+BL32YefP4Iv9
MOIU8TmAvX4kEedI9Qu+2Z8mnEORR0nqBT79LLT/Bh/egh1/Jm0BqMkRJR6H
8Ue5gmug4oGs2QU0PsdVT7A2RRiLhd3ecCAA9geC0QgwlQLfFJJ35fjPKvyy
HE9VkI5IWO0A+oLQVDZ6Vc7PlcCZYjhXTmaL8FQmnkzEE8lwLIeo4+BQFpqs
4CfKkb6ezLYLwwW4OxqOpmB9Ppyvxm8a+NlKJGFYSaariIF513w4mQMNDPY6
aWJCWn7P+s9uPNcv1dOebKUj9aSnjLQXkNY8wG76a/nxTml0jr0Aw620v5EO
qMhEj6gZEMd6xZ5m0lqFOusps6nGMTKlobM6/vWUMKNRdKuwqgx01tFh9pIM
SQyODxDNINWN0MlxkxktLivbfu7RzX23/H6y8pXint/P9wN+eRh0+GH4UevI
Y9Yhxx94/Wbl8NvdByduX/791ulTlidPWx46a/nDpdtfX7Pac/v+hgcPl9g9
VjrZ8W5PoZe97IWDzNVO5vRQ9ugO9/CG7MFNaHsT2t3i7O9zzrbQ/TF0s+Zc
HnLP73OuDwBSKGQKgQUQBWkoRhSRILIr+xIIAhJ5QankFygtlpr++IN46rTs
9Enu8gVw7Rq8eRPfvAHv3sHWDwXrh/z9e8j6IXpkQ21syMOH3DMn3i/AJChU
GRwqBAWSQD8UGoKjYmhSipCcKMRHwKwU2N5MB3v54V7KOqiRHjwxyE8M0YlB
rB+WUmlNP9YwCzokTLwndLKfEYcZgFIFLaaGg4KmB0uC2Es1XUSj5jWdVNsl
LaQ3dOLpbjLbKy2heX9CFp3uJXPSvIZ0TKSumb0h2FjL2p0YqvFkGdYUo8ki
doUdkZipTJENpw7F3eGoMwS2hYCWINAaBFqCocof1PnCUi9Q4M7lu4ISN67M
hSt04PIduFwHLuspirsDC57gPFsu4TwXcQbYfQ79DvMhJ4jH1zL7r+Gp7ULU
rQWZd2HaBWTzC7ZYQH7dJtXxzriNk26SshdkukZRYg/jLqPkC7jwLoo8BT0O
4JjLmBHqfwRY7YRXNsLg32ngYeK4B/ochE6foJCjlMFu9zeQYglrXFCONbT/
hAv6FZY9QZUPQcQZYrsPxVzlR2J4XTxXeR8n/QYK74B6e9zuJhuJRKPxsD+M
1jty7W5wNBRNxMKxaDCZAOdy6R9V9F8q/I9GymzkfCPqisENLrAvDM8UkDfV
8GUVZgyyRG++FM4VsodUlyetBe2MkRYg6SrRRDmvU5H5XjKUT3ri4UgKmirA
L+vQuzZ+tgYZStBMDZqtw8ZKrC1E2hykLULGWmpowDPtwlwf/3KIvBomM73S
JK+mmfZVodYC1JiJmtkfUYqHWugE60gHsKaHYcira3B/ExnvFSZHFANdfEsN
bq5AXQ2Y9d6GcZb94XmD8HJaMdJDm8q5pnLU3y4duSth2Mcsljg+xBvHTBit
LXWLbthf/PaW3y/3Xvx63+fQQz8WR2yCWBy1Djpy3+/Xu24/3XH9wdJl/3WX
/decv7/mvO+683fXnL699vS7Kzb7rlgduHTtpwsnf7307bErH128tuWm5Uqr
O8oHt5DNDdm96zKra7IHV2QPr8hsbsrsHwJ3e85bcrCQ+VgkCtz7QKKI5XIs
yqlcwcvlgkKkcl6U8woTXmFharrQYtUa5aefk8NH8NlTsgtnwflz4PJleOsW
uW1Jbl4FdyzhvTvojiWwYjbViXr7KQMClX4Boo8f8vWDIcEkOoYmJAoxMTgy
RJafTjpaxIEe0q8mA2o8yhRtSBgfwOODaHKEuQsy1geZ258cpGN9hJmNyUEm
fFIaqOljPErrHzQ9TBAlgzrRQye6yHgnnezi9cyOqtH0+6kKfSfRq3lDD53t
J3MjvHQGax/VtkoDpFP1LKRCsvoqNMl6Y5ahlNDxfJ45vZLHqDcSdkfI1BGo
KwJ2hLAAnZGwNYxrCeMaQkFlICr1gWUvuCofWOoOSp6DMjdY4Q2K3WDmE67U
FRY9gul3QJIldt7HPd4NvX+GEbeUP2xEW5Vc4DmTjNso4TyKu0Eu7MFO36Hn
X3MP93L2X8AES9IWJvRGkCoXHHoEp10X4s+jhLMo9QqKuwgdv4DWuzmnfeyT
CVNJnx+5tCtCzDGceQlWPAbZt0jyWdL0gpTZgfBDuN1PHInnVO445yYeCSaa
MKRPpfPZsuFQmncN5lwFDc+p2geORkBDBtDnSKULG124Di/ZeAwypDFlRPo0
9LII/1VL/tOG/9NK/t5C5+tJewTXxn4rDsyX4rf19E09nquCL6sZjHi2FM+X
sz6EDGbg7kSgKSfj5UhTTYxtdFYt/P8snXd0VWXa9rP30/Y+6T0hJIAKiDrl
nXccHR3HBioioiKKIqIgvXcB6RBaQoeQhCSk93aS03vvvaT30BEdp3z/fs/O
vGvda6+TEwiLJL/nuq6n3b5m1ntHuL9iuAve1aDHVn5MCQdpElTBETWiVqSv
A/QIXSfQqIYb0iEa2O8F+XshfDckHIsYdKIeEwmokbkNaOuhrgHoW6BdKqw+
9Lq4qIMPmDm7EtqUyG1EUa8o6ObMGqiVAqMc+O3UTYnoeD7SiydHaAyMNyqg
upO1a+jvVTz9laPD/gAd9r0kEo4f6hV5DCk7f/p6/sbzH22jdXbxjguLd5xf
vD3/422nFm05vXD9iQ/WHXlv7Y8L1uxfsObg/DX73l275701exeuPrCAvv5h
11urd73x7c7XVmx/9autr65Y/7cVa9/9ZtWiVcuXrl745eq/rVr93A/fxW34
BmxeEbPl65gd38Xs2xhzeFfMyYMM4HlAAYwVACRxFLl4WnEJcQmJsXHxfGIi
n5QUm5QSl5yWmJiZmJyVOuv5uHfe55Yti/maMvgd/n4VXLUiZs13YP0PcPWq
mE0b2QOHRCfOxJ89H5t/hs8/g88VkCvX+BtF3M1b3LUr4PpF0FLPWUzEZcdC
lzcHCvq4iA+HPDBKtS/Ihz1TPkEgEYU9KOqfsqBuQQejVCvdqG9q1bXXS6WQ
AogjNi5sRVEHodmwz4GGXFT4BEcqtGd1khFh7y4e9qMh6mDNaEBPBjV4REuG
p376AxLYJ0a9ndSRIs15rm0HdN/AnhvEVcQ6bwHHDWC/yjqLgKMYWItZcymr
uQnkV1lZIasuhKpCVnaeUVCPeoHVXGFbjzGth1jpaabzIGjYyVZvY0/OBydo
BNuEoh2pt/ekH/woVnoKFq8CZz/DJz6CpxczB94Be/8Kdr3CnPyAPTafqduG
wjW4cx868Tp79X226ltc/BmoWsWWrYGH/oZ+fBlUbQBdP8I7K9nrS8GW18jO
1/mqb4lsn7CHrWQpbNlCQx+SHSSjHVyojJR8jo6+wrZuxtEi2H+HvdcKJ1uR
7jhoWsd27mGdV4D/KuivJION7EQ3FyhD2hOs7TzTUwZGmtBIM32yd8XoiZr8
Zgb/tnL/sOFRJbLTb8gl0FsD78rwIx18oMWTMu6uih2jgthF7ivhGLWOFcKZ
lAEljHSjXjk/7oDjDuJrgb5q1NsCxuXovgE9svOjKuEs4YiSjGjgCB0Pu1FP
K+gXo3E9P2gCQzY0ERRNRvBEBI1HuFEfGXDAqJmziNHU7n2sqkX6VuRSCZ0R
ghbstRCHlphk0KJCXpol/SKPHRqU0CCDNg0M2Am1ndSdjvXzw/1JTj0nb2HU
Yuix4l7qRQN8byA26hFFg/xwb2zAJdpwaPU7688u2lq4eFv+h9vPUVn8kCrg
puMLNhyZv+6n+T8cnL/2wLtr97+79oDw4fqf5m84tGAdrcML1v74zvc731y5
+a1vNr+9csvbK3e9u/LH+d8dem/tySWbC5ZtOff51kPLtmz5esMXK9fO/+7b
uatXJq9bCTeviqEA0qIAYqp98XGihLjYhPikpIS05KT0lIS0lPjUlITk1ITk
9ISUrKTUnJTk3PSsZ5L+99X4ZZ/jL5Yxn3/KLv+SWfk1890qZtNmdPBI/LHT
8cdP8ydO4fwz5HwBuXSVXLnOXbxECs7D65dZcRtvMROrGTqt2EddqJfzT7Wa
igT5kJcKIpVC6kipDsKIhwgwelGf8CQR6jm9ZOpDTsiJFFUXjjhI2I56XEKL
tH4X7ndSUwp7rajPwQ26yIgfj4S4oSAZpIpppXmfDOrwiJEb0uJBmj5kWJiR
6wb9EuKqJPIT2HUNeUuApwR4b0N3Meu8Kbz2lEP3HeiauitYV8JqbwDDTWAp
hqYiaLwOjNeQqYjV3QCUwa6TQLiz9DDTcYBp2AUuLGSvLmZL1zG6S3zXKb7p
R0xF8PIytuh7mP8xe3YJc3ZRzKG/MwffYc58xB5+M+bcp6B2I76+DJz/EN5Y
Hle/Ifb2Z+D2cvbcB8y+PzPnP4D1m3HxSpg/n722VLRkDjz4GdLcjJMexeWf
g66dSPkjkOyGrVuIdC/X+B28upA58lfm2sewv5IfqmEnmuEjBeitJt172fbd
rPoE4y9C/iJ2oB6PtOH7CtJTh8wF0HUJ9NeAu13krgROiuE9GXqsxb+Y0W82
8i83mVRjdynw3RLU854CPTKgh3o8qQH39GRCgUfa4V0FHFcibzUItsJeOYlI
UZ8GTfq4cRcJdYBAPRU7MibHdw3wkYObpOOhHIxoyIia5gI4KMc9HbBfDEfV
ZNAg/LyG3HgixE1E8L0+PEbzXZAb8Iq8Os7chVUNQFaD5DXA2I6cCiz0rzRg
q4oyiCl3Fin2W3mvk3OYeL0cUndq1+OQi+sLcoM9eLiPD7pFOhmStQKDEgXo
+yGuNxRLc1Cvn/6BWKs+Z/tPK9/ZcOGDbScpgB9sPvH+puPvbTz6nkDZoXfX
HpxPiVt/+L31R6k1/WDj8YXC89j7G47QN+evPfju97vf/W7nu9/tnv/9vvdX
H1i45qfFG08u235x+Y5rX+0q/mpXyYo9Jav2lK7aV7py94Vvd+xfuWkDpDrI
TzEYF0cVMD4xLikpLi05PjslcXpK0rS0xMzMxPTMRJoHKYBpuZkpM9PjZ2bE
z0ifMS/ptde4zz9lli9jv1+Ntu/mfjwSe+hY3MHD3OHj/Mkz3JkLpOASf/ES
PneePZMPblxDXeI4k15kNlAF5H0ezutGHiekOhjy0fGHAogFEn1cwEkVkH7T
BNXr93Nh+ikXoUhSZZwyqBx9nyojTYVUGYWcKCggLRKxoogN9Ti4ATceDuCh
IB6kPzg312eBQxZu0EBGzdTt4CENGVAIZ3v7ZWhAJiwRmi5jZxF0Fcd4brO+
MuClQamUdd9mA1XIWwN9DchZC6x3WHM5RQ+77sRay6GtgrPfhtZi4KiA2puw
41SM8iyrOccqTjDSo2zLbnBrGVv2LVu5MaZhJy7fEnPlS7ZoBbi+kqnaBIpW
Mle/BFe+ZI5/wJz+hD2/hDnxXsyRBexPb6GqVfjiUrIoD91YRTo2sTXfgeNv
Mz+9xp5fwJybL3jXbX+gkKKjH+GC70XeOm60k1ftBeajwHuVtRfi+tWgaQ3T
vJ4t+Swm/01hxTBSTobq2eF6+FAG7smw/gzbfZDpPggcV0CwBPpLWJrUJrrx
Y2oSOljHNRAspdkNPKTZTUXuStFDJX5MgyE1pQ7wLx+8p8b+22yY+tUmeE+F
6N96YMKUpvtGPEaBaiWUzREJphiG2lGvgkRkpE8P74XguBsH2kCombpQblQJ
71vQUz9/1wrpYDiqJUMqMKBg+1W4rxsPiqk4ckNWLmpEfTah09kYFcReMhoF
Yz1oJEL6vLzbwGlasKQKdFcCRQM0dAK7kndqRWY5tKk5s5xTd7AmFfG5YwPu
RJseU2uqlSKHgYt4+Z4AGYhyfRGR08JJWlhpC7Bq6PuExslwkCpj/FgvDDhS
th9f9s5Gmg3PfbiZYnjy/Y3H319/7P11R99ff/yDDScWbjz54abTH23OX7T5
1Ieb6esTAo8bjlKz+sHaQx/8cOj9tT8tXHd40bojizcc/3TT6c+3nl+27eIX
OwqX7yz8Zs/1VftK1uyvXL2vetW+mpX7axAvokUzIJ+QEJeUkJQsaF92WmJe
WsrM1OS89KTszMQMqoDTklJzU5NzM5Lz0hJnpMbPSuVzM1Pzkj9eGrd5M799
T+zew7REew/xBw7HHj4We+w0f+ocOXOOP3kCnDkNbt3End3xOr3IpCVOG/Z5
iNuBPU4U8PN+D+dxUC+Kwj7O5xaaTwkdGJ1ImCb1cGGn0JyRpsKID0UDuNeP
BQWkMVC421yYGqXxXIiEU4IYptmBvumk9PGDQTQQFNYT+4XDFPyAAQ1byLAR
D+vJgAoKZ+3lsQNKUZ8MBmqwi0reLeC5LexYo09nEQUQ+muQn/4uNUFfI7QJ
DbWRvYpzVSJXFe+uiaemy07/ZBnwVEPlVdh9ljUUAv05Vn2WUZyGHT+ydWtR
41amdQ/begiUbWOufQ2KV7M3v2ebdjGVP7Dlq2HxaubMJ2zhcvbi58zZxTGn
FzKFX7Bd+8DtbXE7F8aeeJft3AW69uEby9izC6ikMuc/ZE4vYPa+CmhdXRp7
fjFXux237hNZ86HzNLSfYl2XUcdW0LEFdu8Bd75mLrzPXl7M+m/igRrYV0km
2+ETLQpVAtkxIDvB6s4w0TskUML2VOHxTjKuQI/teKgb+m+Dvjo40Y0eabnH
WsFhPtKQJwb81IJ/teN/udC4BAcrGaqbwx3ogYbCK9xRf99IHlAMFXC4A1P1
pE9/HYyIYVSBokquXw8fhMiQBfvamVCb0AV7XM/dc+DHQf6ujQwpwKjgTISD
Lf1UkacOFY5Z+HG/qNcOeiy4xy4Mp//tLD8aFZYehsOikI0YpVDWALproLQW
SutYnRjZ1NSRApMcWdVE1S4cBHCa+WAgwWOPpcKn6IQmJfY7YyM+6j8F7fO7
eI0UdDcDlZjx2uOi/vhogOuPxg0NisKunEP5qxduubJ4W8HibecXbTu7aMuZ
RZvyP9p85uOt5z7efmHJ9oJPtl/4eOvZj7acXURhpJ/adPKjTScWbz61eOOp
xZvzaX286fQnm/OXbspfuuXM0i3nv9hesHzXRcrgt/turdp/fdXeom/23v5q
Twk3JX98fHxCUmJqalJmWlJOWlJuRurMzJRnMxJnZiblZSXlZCVlTUtNn56R
kpueOCM9YWYGraSZaXHT0+b+IXHNuthtu0Xb9vJ7DvB7D3K79vP79vMHD3GH
j4mOngAnT3DXruJOcaJCHafXIYedOJ3YYUMuO/JTa+EibjsMeKgppdaUUkn8
bgogdaFcyM0F3ITKYlAQREof1UEcoQB6aKAWpk/7fDQnkh4XH7bjkI36Uj7q
5no9aIj6z4Cw06aPSqSVDNtFg2Yh6VMGhwx4UIP6lMJGfWFRWIl6xZhC5ymG
3lLoLYO+CuguA+7bwp4Zfx0KNsEgzR31yFZHbLXYXgU8VchdRTFEFEb7Heyp
Aa5qLL/Iqi4C81XWVMAaCxjteVZ2HFLL1/kjKz3GduazJZtBMeVuPXNnQ4z4
INu8mW3azt7ZDC4uZ6+sjLn8FVO4NObsp2zFatB6lDWUxfVLEtv285XfMu17
2PqtqGg5W0ql8wumcDF7+G32xzdp2GQrvgXHF4neycKyQ8h/EXsvQt81qDwI
OrczyqNM3Trm0iJweTFjL4Q9wiXz7EANfqjCVNoM57H8JKM9B503YF89DpXB
4WY4IkYTGvzEKRropLGUHWkj99X4qRk/MaIHWvizkXtiwk+t3C9O+A8PGZWA
nlrc24QmFeiBgcILH9m4BzbuvhWPU1MqBpNSPNRJAk1MRIHDShxRckMWdD/M
95mBrx0LR+nVaMJE7jnxkyA/aRFuHRnRiAZUKCoDvUrcS12KAo7Z8d0wP+Ql
UQsKUk108aMRbjgkSOFYLzccEa6v95g5TSeWNiJxNWwvZ2T1FEBslhOjBJoV
SNEBJE3UcJKAVxQKxFkNRNnFUkF0moifDtruuIgvNuQXWQxI3gElzaxZg4QG
oIJQpo4N4bA/e/uxLQu3Fi7ZeVWYGt12afFWymPhku0XP90xVdsLl2w7Txn8
v9p8esnWM59tu/Dp1vP0U5/tKFy6tWDZ1kJK32dbzi3bWrB8x5UVu2+u3Htr
Fa3dZd/uLP9mZ9nXO26JEhNiExPjkxOTU5Mz01NzMlPyMtOeycqYnZ0+Jyvl
uazkGdnJOdlJmdNS06anJ+emJsxIjZuZkjgrPXkWVcOMuNysF38X9/nSuA0b
8OYtaMt2vGM33r2P23+Y++koOXgIFhbi5rZEmTJWZyRWK6Fh0GJBbhfxunmn
VSDR5+ZoMPQ6iN/J++w46KLQ8X4qkS48ZVBRWEBPyIZRDzcFIO71cr1eYVom
6hYuMw9RKXThqQULTthjE0ADfo4aVOEgp4MfspAROwUQDZlJvw71aZHQ41WN
etWgV4q9d4QTE64SakGR/46AoXALdzkI1uBgMwx3EF8zstcCZxNx1EJvHfFU
AepOhe5O1cRbhwJN0FwGlVeA+RZ03GJtV4DjOrBegppTUPYTQ+VGeZYRnwU3
17BV29jqLWzjdqA6Cbr3g85DbN0ecGM1KF0vHNa7uoK58DlTvQm0HeNbfsKj
cpHuIurYwbTtZstWsRU/MFUbmfI1TPlqhorm4fnMmUWg7DtUsDzx4o5E7dn4
aAUzUId6q4HyMBTvZrSnIYWXCijVQd1p6L8FvDdpAKReET3UkVAdlJ9mtQXA
eJENVKLhNthbyw63k6EuOKkFP3u4YTnb3wrGpYLV/MVOfrGRxyb0s4U8Mgud
WX714N+8/KRSWFbob8N3tfiegTyyk4du+NBJHlip1USjMjQuQ6MSLtQJoyoS
VaOoCtJh8H5EOO0S7II9EjJCU6QV3XeTJ0HuvpMMqtkhalE0OCoFPXLUo8C9
NCQa4YSfjAn+k/iNMGzGdFwdCvG0BoJ4JEoGQyTi5pwGTteNpXVQfAe1lSJp
HTB2UxKxXgZ1XUTZgpTtyKwlwUBsMJikUWBJO9DLeZcZ+Z10kOepELisvFaO
upohhdFu4ntCov4IP9wf5/ekHj63dtGWG5/uKPx0x6UlOy59vL2Q1ifbLi/Z
dvnjrZTKCx9tOfPf+njLmSVbzy3dfvHzHZeW7ry8bOflL3dcphb08y0XPtt6
gb5YvuPyit3Xv9ldtGJn8dfbbi7fevWLLVc/33Q1LikxMSU5OSUlLS0tOzMt
Nyt9Zlb67KyM57Mznp9GSUydmZ00PTs5i4bB6SkpualJealJM9LSZmRk5WZk
zEhNnUnZTMublfL315JWfIXWrRdWKHZvJzt3cFs3opNH+YbmFLEkVq3ndSak
1QOjiXM6RS4HdlAAbdjjoDpI6IceO/FQAJ0cHaAEiXRxFEOaEKNTLcKFmkqI
Qir0CTOlNBVGXCRoJwHHlCy6hLWMfqp9ASEzRgUAuSHnf9cKabigOsgNGHGv
Dgl78jW4RwP7NMRXj1y3oaMMuMpo9KM8UhGErlLWVwWDTSjUifwd2NEIXI3I
WQ88ddBXi311wFsHPDXQVQODLTDQivTFjKEIeCqgl1pT6mnpF7wG9aeA+gT1
pazuItt2ir32LdOyj62nTO1ljedZ9TGGUtB4IKZ0E1u7l63ewRT/wJz/nL2y
jHQdBd0noO481J6F1gug+yfKHajdyjTvZZp2s+JDTO1O5tQS5uJSpnI9rN7O
26v5B2bRUAsY7gA99Uh6NEZyiNXmA8UJtuS7mMJFrOwn5LjCOq5CayEIl+N7
ajKhBcbrUHWBNV+H9iLQ08QOtKC+JjjWxY1IwEMbeOoTjarBsBTcM6Kfbfgf
TvyrGz+ywCc2/qEZPbKhX/3kVy+ZVKPBTjjQQe7rufsmQPPdQxd86CL3rNyw
CowrBQwHu3FIDHq1HMWQfudHXeh+FPWacaAb96nQmAlP2Ml9F/w5wt33kgEd
GDYIVyKE5SAiQz1KLqrEA0Z2LAjGe6j/5CN2zqfHISvs8aDBADcQ4AQew6Ie
H6GjNzWiylYkrmGbboGWEkTRM8qxUY70EqTqxF0NrKKd87gSw5EUk14kaWWV
XchmIC4b73Pybjt22YlBy8s6gKyTNetQJMT3h+MphtFA9qEzX3206cYnAoMF
1IJSI0oxFOjbep5a00VC5dN4SLPhkm3nPt1eICjgjotfbLskMLjj0hfbCj/f
VjiVBy99sf3il9svf7HlytJNBUs3nv9kw7nFP5xOTUlJT03LSs+Ylpk5PTtz
RnbGrGyKnsDg3GmZz2anzcpKystOyclJy5yekpaTkp6XljEjPXNWRubMzGl5
GVl5KTm5Kdl5qel5qbPnJrzyOr/gPfT1MvDtl8yBfaSmKbGtM0GuEqm1vFxJ
dEbe6uCtFmI1YacN0UhIMaT/dycl0Ya8TvoNocooOFIqi8IUjZfmRCwA6MZB
Koh+LuLnwh5hyjTkIn47dRQUTCwoY1CY3eoJIBoYIy7qW8iAAw3Z0YibDNjx
iIsfsOA+gUHcqxUA7NWQQDtylENnOXTcptAhTyVwV0JHOXBXQX8DCrSBsES4
c8/RDNyNyF0L/PXIQ5+N0FcPPZTEJhjpwu5GaChh6RcJVQmHCKih9d+hJDLm
80B7mtUXIP01VHsopugHVnwYNO6OER9i7ZdZUz7QFsDGg8ydnWzrUablIFu6
gT31KXttJdKeYzX5UHWKoZIaKAbSE2ztDkD5FR9lu4/SLyhctXHte3B9BWjZ
zXYcZLWFeKSLTIrRWDfuacGyk6zsGKs7CwwFoGYre2ERaNkJjNQhX4Tac8B2
GYx2oocmPtiIVedZcxG0F1PXjQfacX8zO9yGhVUGJXzi4p748agWThjIzzby
Dxf6jULnwY8tFEnuIRVEB/7FR35xkwkVohFyuBs+NFIvin8Nxj5wooduMmmF
Ixo4oRbmS/u7YEiKe/SkVwcGjFP3xoS5EE2mUjyoFe7Eu+ckk274uIe/6yED
WnbIjAdNXFhC/xaKqHFUhYR9hk5uOEhGe3G/X+jq4tYgvxkJG6gCVBCpGopo
vvM7kN2AFWLhgqbmMthQzHZUQWUHp5djg1K4wLa7SYh+DnNcNJzidsYqukl3
O9QpMRU+p5lzmIjDSuwWkVKCu1uhXkXCQdFgJG54MCHozd538qsPNl4RVu23
naP0LRaeFL3TH246+eGmUws3nly44cSHm08u3naGutNPdxQIDG4tpMTRFxTA
pduoKS1YtuXC0s3nlm4++9nG/CXrTy5Zf3rx2tMLVh2i/nNaVkZuVuasnGnP
TM9+hnKXkzV7WiYF8PlpWXOzMp7JSpmRlTI9Oy0rJzU1NzUjLy1zRnrWzIxp
MzOm56Xl5qXOoM8ZqdkzUjLz6B9ISZuRljsnYeVXsVV1KU2tsd1SkUwtksp5
tS7WYOH1RmgyIJuZOGz0v4yddgFGl1VQQ4cVCmDasc9Ggi5hA5vfhalTnerP
yId8ooiXFyZnvCTkFOQv4KQ8EqHPeIjvDcb2BPiID4edsM9N+oRzhcLp+wEn
GvLwwk42k3C3TJ8hvseUFNaAUBf2VANHObIWs56pyU9PFeWRdVaw/gahhVNY
gj0d0NEMXc3Q08j6KHp10NuAfM3Q24Q89SjcicMyZK6C1nLoqxR2nIbvgHAl
DFcJ16dYCqHuDGO4jFTXQelWpmob6DrONu2NoRy5r0HHRWC4ChsOMHUHmO7T
oP0Ie2sDc+YT2HmIM11k1WeQsQAESkG0FsjPgbp9jPgEqzjLKs6xjmLWXYpr
98ObqxHVRMUpxn6F7atAk2I4LsX9Yqg6g+UngPocchaxkmPoyhdM2fdQfQqo
8oW9dspTTKgSjqvQqIaYioDuMnCWI28F6GnghrvgQBsak6ExJZzQc4/d6LGH
jBvgA7voqRf+5kf/CuFfvfixDT1xTnUoc5BfvNzPbjShR4NSPKoQpmUeu9DT
APfAgx/68KSdjGiFjDkhzHbCiBJF9KiX5nELGg/gsRAKakiIuk0TnHCSuy4K
IHoc5e568YAeDxqoaRGaGgRkKKwUrOyAgQgHKOjPNMQPR/geYWoUOXTAa+ao
F+3zc/00xAX5gIuz6pFGAiVNqLUS1heBxlLQXg3U3digwkY1UrTD7iaolWOv
J8nvS1erY8VtgEJn1HAWLWfRC43PrGZeQb9CK9bJYNjD02w4MpTocMxc++O6
dzcWLN5y4qPN+dR5UgApeu9vPP7ehmPvTc2aUgzpm4s3n1uypYCS+AkNhv/N
hpvOLtl89uOpKZqPN5xesuHUknX5H/9w8sM1xxd8d+jNZVvzqKPMynxm2rQ5
ubnz8qbPy8uZl5vzQu60edOyaM2ZlvZsdvJMiuG0tNyctJzc1OnT03Jz0/Py
0mfMSJs1I+2ZvLRZeRkz8jLzZmZNm5GRmZscm5v0p1ezLl9PbWqO7+wk4i7Q
LeWVuniVNlalRjodMhmI2YipFNot0GphHXbqS7Hd9n88UndKRVBoQCxcOZ7k
pe7UCwJeLuwSvtthIS0Kf4ACSBUwSlUvREM0Fw0KeIbtuM8rmtrITQa8lESW
Jvp+G+4xUf/DRfU4aqAjMKDsuOugoxJabgNXJfHUUmnDjgpgLwe+WuhvASEJ
9kuQowW4Wom7hfiaYLAZ+RrYQDMKtgP6YbiV65UBCqmlGjlrhI5O0ToYrqbB
CkdqkK8EmS6wVIlMN4GkAF1fw7T8CLqPMa37Wfkx1nMV+oqg9hqsPsA0HQOK
C7D5MHvlO+bGami6zGkvCI0RbVdhtAb0tkHpeab9MKvIZ3SXkK4QesvZUAOQ
X0VFa2O6D7H689BxCQyUw5FGZrybDMmQthAqzwLFWeCvwJYitno7c+Uz0HWY
amiM/DTsOswYCmAPzXoaLtQG1VdYGmP9tTBQy/a2kVEloNZxTINHVGRCTyiD
j3w0spHHXu63AP4tRP7Vg34NoIcO9NQveuIhTzzo1yD3S4CbNIEhObpr4O7R
wOgDT4Lknps8CuKHXn5UA8fUYEJH+iU4ohXu4+0x4j4bNxkRjYchVcOwigxa
+HGXcI02rSe9ons0zptAP82GJiE7+LqFvucRlXCqt4eaWAOM2IQTbQNhUcjL
Ow1Ch0EXjYouTpi485Gol3ObsEGB1F2E0ldfzNZchw2lUNxA0eOMWqyV8bJ2
LG5iDBpROJzutCXLxFQQha3LWjmh8mdQ01/IOL2Wk4spzshtRf2h1LHBZLcj
e9P+VX9fV/jBluMfbDr5wYbjFLr31h9bsP6oUGuPTC1bHBeWLTae/mjTqcWb
hKdQG08u3nRqESV0/fFFa499tO7Eoh9OvP/d4Xe+2f/6ss1//ujb6Rnps7Kz
Z+dQ+ma+NHPG72bl/S4v90WBxOwXcqgdTZudnfRMFsUwbea0lBnTk2dOS56V
k/JsbtpzeenP5WU8l0sr85nczBl5GdSapmVn5M5NP3kmsa4utrUtoa0ddYiR
TJUgU8VKFVipIjotLWQ04SkMoc3Gmc3EQp0AlUUKIE2FDuJxIq8wR8p7HLEB
jyjgEaZMA1T7XAKbPgfno2DSbBgQVvaDPiqFRIiKLtLrEUUcsJ/Kn4fQMXPQ
x/U7KIC4z8JHDThsoEMxDCuFeU57JWupYB3V0F4FfM3YWQOtFdB2B3gbkdDO
SUk8XdjZAj1txN0M/K1U/lCgHfvboVCtoFdK+pRCVHTShFgPok1Q6CZTD3sb
UbgaeEqQ8TxjugzNxbD5OLi5juk4DMRHmfaDjOI4470C/cVAcRHVHIxpOwmU
hYCqYcE3NB5C8zVWeY5VnmHdN0FvkzBn23WOFZ+GqgLGcBUZLgPvHeFiQGMF
ur2F7TzAmguB4xI7UAmH65mxDipGyHBVMKuycyBQg701jPwCe+VLqr+o/aAg
wZ2HBU/rKEGDXWRIheh3wHATuKpAsAkG6iGVsxElFlq0aIVuHfcs+GmIf+Qn
1Cv+EiS/RfA/e+B/+snTAH7ohk+DhPrVxz70W5T8EkCTJm5ABu/buLtm8nOQ
exRC9wLwUZBmPX5Yg0Y0eFzLhWWgx8CHjajHLBy4vtsnXJjmV8OwRrgRaMLL
TXi4SR983EsmfWTAiHr1sN8k7Bf1SEBAgalo9pm4XhsXMmKfDgetpC/IU69I
U4lFhUwK5Dbz1CBFaWYRcgpv0WC1BHU3o/oSUHGFqb7BNt9hpe1Ip0RU9dRS
TtzM6OQkGEzw+xPVcr6zjZV0IEUXUXUThQQbDCKjgWjkUC0hDmNcbyh+bDDe
Ykpfse/7t9ecen/jMSp/VPsWrDuyYP0R4fnD4ffWHn9v3XH6+r31RxdSWVx3
9P11xxZSMNcLz4X09dojC9ccfn/NISp/f/9m/2tfbH15yfe/e//z7KyMvGxq
Pqe/kDfjxVkzfvfMzJdm5L04Y/q83Kx5OdSOplMGn8uiGKZQEmdlJ82alvRM
TvJzOSlzpmfMzc2gzznTs5/NS8vLpXkyPTEnedPGxDt3khoaRM3NqKWV75Il
dsn4bglRKDmFCqvVSK8nBqG7IjSbsNFETOZYCzXkNkofR8Ogm4qgi7gc0OXA
Qg+OKdXzOYnHhdxORKMiBTDgxBE/H/bzQY9gRwMOEHbiqJujAPZ5yNQVInjA
y/c6ScQiXL8cNeGwno1QBjXI3gDMFchWxTpqoL2adddDmulslcBcDhy1yNvG
hRTYL0OOVujuwK426G0H3hbobUP+LhQQI087DktQnxpFlLyDpsJ6HGoEfS2I
MtjbgvqacZh+zWJkuMBargHDLVi1j7m9mek+ATspg4cZ2QnGcxX4SlhxPqw/
zIhPA1UhW7mHPf81kJ2FxstAnk8ZhN5iMNCGI52oPZ/tLoDqS4zpBjTdYL01
JNKKnHWgYhfbvE9YB3FeY3qq4FgzHG2F4wpkLgLqAqAoAP5q4SyD4w6o3MGW
bwCtP8a07GdafxLaf6vOgGA9HlaTYCc0FgML1dYWFG6hbwqbzUZUeFyHRpSI
wkjD3S89+GGAPPST33rwP6P43wPkn70cRe+RHz4Nc4+D+OcA/C1K38EUtCEV
eeDk7zngr/3c/SC6HySPQ/C+mwxpybAKD6mnMKTu0QT7LNyAm9wb4vvcyKOE
YR0ZdnITfkoinvAgqoajbthn5KNaGiJQVM95JCz9oQRVsMeKe20oaiU+PXFr
YdAK+oN8j593maFRxZrVQpAJuTifDfntIpueo0ImbUP1ZbCskCm7yNQUsR21
WCURGbW8Tkkk1Gm0IZc9ORRO1+lE4jbU0YQlbUTcykk6OLWCN+tEOhVUiAFN
T72hhLG+JK1y2hfbNry1+uyCDYfnr/vp3XVHaM1fe3j+mv/Wkfk//PTumgML
1hyaP1Xvrjn4zpqD764+OJ/W9z++s2rvW9/u/tuKXa9+ue3Pn/7wh4XL5779
UUZ6+vTszGezp82bPv13s2a8NHPWi3kzXsrLnTd92rycrLnT0udkJc3OSHgu
S6jZ2clzslNpzc1Jn5ebMS8vbV5e+tzpWc/kpuTkpadmpixaknazPK6mKrGx
Hjc18x3iuA4x39GFJTIik2OZnKhVWKtGBg1PtV5rIAYTbzZxdjPndJCp+RlM
g6HTSlxUEJ2coImCMlJNxG5awvQppvFQWMT3igIuPkh5tE9Nywg6OHW2VzhY
QQHEVAcjVhKx4rAVCQbGiINqYmtAxgpgqQb2OmSrFrqN+FqxrRaYyoC1Erua
cFCGg5TTTuRsxy4qhe3A34G9bTAowYFuIHQ5FONepTC94+oErkbob4aRFtjb
jKLC5n/Q30odKXDcZA0XgfEmUF4DJduY+j3UTFINiuk6wkhPsJ4rgFrKxuNM
3VG2+xyrKGRLtoLL3yLdRaC5wEiOA+o8/WVgqJsLtrHtp4DiEtReZU23oKmY
9dbiaDPrb0I1h0H9PupFWc8NEK6AIy1wrA1OKqG9BGgvApUQ9GBPC/bRKHQD
Fq0CDbvZ+t2g6RBTt59tPcQYroFIJ6RoOGuh6TbwNAjtACJtKNKGR7VCjenx
iBqNGvCjAP6ljzwM4ScR7p+95N996D9D5B/9mNL3JIh/7SE/R9DTMP41wj90
ckNaNGrk7jnIAy/+ZZA8iFAM8cMwd89DhvVwTIsGVTikQFETiVpw1IYG/Wiy
n486kJe+rxOuzr4b4MbdaNyLHvZyo9TYGEhEAyOCh+E81PzThKimoZKE9DBk
FQ7weg3Ercc+C6HBLSBsTiMGBbZoOKeReK0UQ+wyI4MSKcWotZqtvAZKC0H5
JVB9C3Y0Ur3DagUn78LyDmzSivz+NJs1QdbNdTSRjgbS3oA6W5BKTix6kVHN
UXG0m6jvSp3s5zrEcz7duOvttacXbDw2f8OJBetPvLv2GC2BuNUH3l69/53v
97/1/Y9//37vW9/tffu7vX+n9e3uv6/c9caK7a9/vfXV5Zv/snzry5+t/eNH
K15Y8Nmc1xakpKVRKZyRlTUnJ2fezOkvzaQimPsCDYbTpz1PI2F2+vOUu4xE
iuGczIR52UkvZCdPVco8iiFlMDd9bm7KM9MzszOzXngh6fzl+Erhfnu+rgE3
t8c3t3Gtbbizkxd3ibq6sVROFFTcVUShEim08Vo9r9djs4l6UWQxAqddUEMa
Ej3CBCl2WimSnFt4kzpVzu0Q0dc+V2zAK/K5KaEUTxRwUPr4gB2GnbDXO3Wc
0C3MWgt7ue0kbEP0GTCgoJ6nRtRYj7SlyFrN2epYSw2yVENfO3I0AVM1MpZD
Wx3ydIKwDrulxEYVsAs5O2jiA952FOhGIaHnGva1w4gc9+tRWMPbmym/KNSO
o+2wrx3R7NbfDntbYKgG2G8C0xXhSof28+DWlpiOw1R6mI6jghuUnRAOvdrK
YPVhpuEE23UBSArZa+uY8i3UaiJpfoz4mLCkGKxGw3Le1cC25QubcHTXWRPN
mMWsr4F6URBqxU35bN1+RntOcK3hckAZnOjEk3LgqRAY1BXRf4LtEwsHGXz1
sGonLF0H63Yx9XuZuoNM9W7QcUwIv/1K2K/CljvQUQMiYuHy+XAb6pOgcQOe
MKFxIxlQonEL/jlKng7gBxH4cy/51wD+zxD6zyj5Rx9+EkJPe/BvA/wvNCf2
QQrjA1fsgAqOW8mEnaon/+sQehgRBPFhGNzzkhE9HDVwfVoSUsMIdSZmFLWj
oSC8NyyK2jmPCoYNeNjDTYTQmJcb8/GPBiGlssfA+RUwqAZRA/HJgVdKfSkM
a3mnDLjVMGjBIQfnNmObRtie7XcIy/FCS2sl0iuIzcg7LdhmQCY67CsEQWys
QBTDm2dRcQGsuw0oieJWpJJBZRen7EIOm8jvS9Gq4iiAjVWgoRK2NiJZFyfM
2OgJjYcGA9Xc9LGelI7Wl5Zu2P7W+jPvbTj13vqT8wUGj7675tDba/a/uWb/
W6v3v/ndvr99u/ONb3a8sXLH699Q9Lb9dfnmV77Y+Bdayza+/PmmPy5Z9eIH
y55/c9GzL/89KTUlQ1gWzHwuZ9rzM3Lmzcp5Yeb0F/Omvzj9v9MyGZTB2ZkJ
c7IS52UmzstKohhOVcq8aWnzpifNzUuZnZs8MydtRk7ylu1p5XcS71SIqqtj
G5rjGppFjU18S2tsW5uovZ2IxbSwRMJJ5JxCHadU84IgUl+qxXotspp5q5FY
jIgSZzcRp4W4HbzLLrLbRHZ7nMOR4LBzPm+Cz53gpTlxClKfHYfp99yKIs7/
LheiqAf3B2KjLkofLRx18gEj8utpguAMDUR8FZmqsake2ZqAsQq42nhXC7I2
QF0Fa6nF9iYh+9MB2UZFUAI8UuLqQN4O4OuEISkIySD1or5u4cahQRMSCG3B
gTYY6UC9nWCgiz7hQKfAYKAWWouA8RprLYf1x5myHazsFEMdZttRRnoMSI/F
OK5C6lErDjNN+VB6EXRfYC59zzQcQpQd8cmY9mOs6hwTrAUDCmKugm1nkPIa
q7nGmEqwqXgqrrYKpLQVsjX7Y9RnhWMdgXI42AImuvE9JQ5UQV0hNFdgWyns
74b+esogq7gKilaD6h1MNcXwEHtnp8Cv+jL0t6BhPfZ3QnstG2iFNND1SVGw
GY5p+AkLnLCRIQ3sU8IJB/m5Dz8dIg960C8D5N8j+D+j+N+j+FeKYQT90of/
Mcj9MoD/NUjFEd51kiE9uu8RTdjgkx7uKVXDMJoMCC2WJr3csBGMmrgerdDG
OkijgYXrdZCRKDc5IArZgYdmQxMapHY0yA+58FiIPOjnh9woYiBeOfArEbWs
Hjl0S4BPgT0Kom1izZ3IqgBuA/ZZRU4DNiqBVct77LzfK6K/SDoVMqg4mz7W
Sh2XEupkWNWFWuvg7Wvs1Xxw/QxbXYza6khrLepuRRopUXZzGhox7CkGXWJH
C1dVAitvgaYqJGnHBiVv1mNZJ9ap+VAgfqQntqLmpYVrflqwPp/q4Px1x979
4SgVwXdWUwXc9853/8fg6yu2/fWrLa9+vfmVLzf9ZdmGP3++7s9fbHj58/X/
88nalz5c/sI7S2b/9d3c/3k1PjkpNT0tJyvjmZxpc/NyX5iV+8KM6S/lUgZz
qBedNz1zbnbKnMykuZmJQmUlP5+VRGtudvK8HFop83KzZ+el5qZlLvsy9UZJ
YkV5fPkdXN+U2NAQX1/LNTbGNTbHNbVw7e1cZwcvFos6umIlykSpglMoIGVQ
o0ZqjTC8GPTYJDBIKIlWk8huiXXYY+1W3m6Pt9pirbY4jzvB44r3OGOpTXVZ
6YjHBWhZqQIK20ojTtRDAaQk0gzo4CM2PupEAQsSlnTNWN/AVR5G6gpkqGWs
rfQJbU2Yxj1bM9RXA30Va2mA3m4SUHHmTmgVQ7ccurqpLFIGYaALhhWCDnrE
IKTE/UaOeiFBKNtQsENwdP3duL8L9XWjfjGKCod0WAvNbkXAVA6rf2RqdwuL
AtJ80H4CdE9t57ZdE9ArP8I2n6EvYOd5cHEN251P5OdA+/GY1iMxmgI21AD7
5UhThlrOsJRB7Q3WfBuZSgBNr6FWFBFj6U1Q/SOrPM+6ioG/HE6tsKP7KjTY
TgwXWWcVtpfCvk4cbIKeakBdd+0+XLKBqdzN1v7IVu9nKnYybSdYSxmOSsCA
gThbgLcZ90qoLIJoFx8VgwkLN+nAVAT7lahfi+764T+GKVCih1H4jyFCAfx/
4+jfY+RpH/65Bz/t534ZIr8N49+G0OMwGrOScRu67xVadv4ygh/3o3sBftwN
J0PchId+TepXqRSikJnz6kHUIoo68FgvmRgQ+YxC5+WojRvxwrGQMJ82Ltxg
T/qcMKTj3BLklcOgBruU0CmFPoXQjUtWBRR1xCAmZgWy6aHTzJvVQCOBBiVx
2onfm+i0Jpi02KABJi2i4qiWYlpdrbCmHF07Dy4fZ0ovg7oK2EQlrxao5CKV
lFdIsNEQazaldbcnl92AxVdQVQk1qCKtMs6gEakkPMU8GkrpCyQdzf/g9e9P
vrf22IIfjryz+sjb3x94c9W+N7/b/9aq/X//dt/fvtn1txU7X12+5eUvpuj7
fN3/fr72f5f+8KdPvvv9ohXz5n86+28fzHz5jWm//zOfnJicljYtM/2Z7Glz
p+fOm5E7Ly/nhbycedNzns/JonZ0Tnbac0IkpBgmz81KeT4rZW5W0pzspOdz
UudNT3t+etqsjLQPP0i9cC2luDT5dilXWR1XXRdbU8XV13ANdXxDA9/URJqb
SWtLXEtHfHt3nFhCpDKkkBOlHKtURElJ1CCjgTP8d67GyJmtsSZaFpFAn1Vk
syc6HElOe5zTxjumtrcJszQ0dNtw2M2F3DjogFGPcLIp5EBhwYJSfUQBM/GZ
OIqhtBIW7ULdN5C+DpibobkBUFPq6EAW+pqGggpAkXR0Ap8auRXY2A5tEuSS
YsGIdkKPGAblOKjAPgn0SGFUR/otmP4mOMXIJ4bhLqGBxYCMoxgKTbe7YKQZ
eu6wxqvCRIfiBlOxm2k9ANXnYfdptvMk23ksRnIY2G7C1jNs+VGm9TyQXALN
p8CVjay6gIhPMS3HmObDjKYQBOpRrwRJb8HWCwwNlerrNLFC423gqIGBVhzu
gro7oOYQKytgXaUwUAF76tGwGN5TwQcazl0C3VXIWgGi7Vy0HXmEuV9GfROX
bmYrtrGVu9iagzG3tzPV+9mOs6y9GvVphCvm3DTzdv3fLr6oFPfI8KSTm3Sj
MQvXo6Kcogch8ssweTKAn/Thfw5z/xnD/5nE/xzF1KY+6cVPB/GvI/hf49yv
QzQAEmoVJr3krod7EOJ+nUAP++Bdv2jMjSd9HAVzwoGHqA7qRCEb9Btg2MJH
BAz5kajIraNqiCJmTNVwNMD3O+BogEz08b0u5NdS6KBbBr0a4lIiBx0kZdgl
R+oW0FnNdtVDRTsySpFVjW06YlAhtQRqpdhmjPW4EtzOBIs+XiMTySVYJcXK
biQTo85WUnkTXjvDXMkHpZdR1U2h1Yu4Ccm7eHmXSCbmjfrk7s7E0mvk6lm2
5BpsqedoWlTJYvWqOLuZ7/Ol2CzZK/esfnPVqbeo/1y1541vd7/x7d43vt3z
t2/3vLFyD2Xw9a93UAb/vGzdn5b+8D+fr/nTZ2v++PGq3y/66sUFn81+Y+GM
V96a/j+vZL34R5KUkJiakpWRNlOYHc2Zm5cjONKpVcJ5OdnPC9M1Kc9SBimA
6clzMpPnZKXMzk6dMy1hbg7FMPu5jMy//jHt1IWUm8VJt4q50jLRncrYO+Wk
ulJUTVNhNVdfzTUKJIoamuKaxUmtnaRLDCRdsEuM5HJeruTkCqzTcGol0Wh4
vSlWZxHpzCK9RWSwxhkpho4Eiz3RZol3WDi7GbmsyOvk3BRAh7BRMOTCfhuM
eEURD+cX4iEXtOOonfjMUGhhbwfqZv7cRtBwXtA+fQ0wNkJdNXB2Eksra2wg
2irKIGtsRi4FcmuEq/CoDjpl2C4G7i7ooeZTjgNq4pVCVycIqHGvEYf1xEWd
apfwGxsWg14ZHpBjQQQlwrUYoWboLIMGakSrYOtZ5s5utvM4o74AxScZ8Wm2
7SeGRkJzMao6HlN2lGkrANLrsPkkW7SNMghbj8Y0HGEaD7HqS8BbC4IdqP0K
23oRKG8A5XWWAkgxdNQgbyuMSJClAdQdiZEVAEcp8N8BEeFyJDgpnOnD/U2Y
cueswaEW1CdGHmHZBViqQMtxWLKBrdjOVu6LubOPLd/F1h5hZJeRs4kdspCw
Cvm6cI+S9OtBr5oLS4Vbdyb9eNJDhs1cVI6HbaL7Yfh0mHvcT54Ocr+Nc/+a
QP9tDvjzAHrUi34dIv8cx/+apJqI74X5ISt8EKJ/nX/cD34dw/eiQiOJYQca
dZFxD7nn5XuNbEDHhaycV0e9Ch+2s+N9/FCEc2mgW40jVq7fyw35+R4bGYkQ
+qmoQ8DT1gUcdDxUY7sS0p+Xqxv7zbxFSyRNbEsF03kHKpuhrguZqaVRc5RB
pRiqupFwaYMnwWkX+nyJW2kGFHbCKDqRohu11pLSK+DKGfbGWVB6CVYWoYYK
JDDYBTubkE6dqJTH3rjAnz0Cii7DxjpRawORdQo9+xzm2IFwfF3979/8Zv/f
V+3866q9b6zY9trXW/9Ka8VUfb2F1itfbfrzsvVUAQUAaQZc9OULCz6b+8aH
s159e/qfXpn20v+kz3lBlJiYlJaanpGak535TG7O7LwpAHMEBqkIUgb/q4PP
ZSY9l0FJTH0uK+UZmhCzUp+flvj8tPQ5Galr16deKY4vuplYdIsrKRfdLiVV
5VxlGV8hXKzN11SLqmtia+rimtqSmtuoKYUd7aizHYm7+S4Jkck5pVqkkmOl
UqTWxmkMsRqjSGuO1ZhEOkucyZFktCWarHFWC2czQZoBhX19VuRz4iAF0IkD
DhT1CvvWfHYqi8RvpZpIAlSqjCRoA7p2rnAXvLIbqWsYTRV1pFBbw9paib2D
wgj0dUh+G6ipL+2iDGK7FOnbgV1CB1hBFt3dQuffoJoL0OhBeZQgSl+/lfeo
kFuG/P/tKEqToJLrlcI+6uKkqIcmxyZkKwWGIqC/jasPM1X7Wdm5GMU50HGS
7T4jrAt0nQT6W+j2kZjyE6ClgJEVgaYTbNluVnWBbfqJqf+JafiJpUmNQuRu
QY0FMa0XqZ4C5U1gmNJBey12t4KIBDrbUdMpVlYIhJuU7sBwHRAuaZGiewZ4
TyEK1AqLJjTZ9XVDXx2iydRcTtS3QPl2ULaFKd/FVB5gy/bEVB9kW06z2hJh
L9mIg/crQEiFB4yIqlivHkWUaMItojnurp+jPEYUQpPHRxHyy6joQT/8eYT7
5wShDP77Lk8V8Of+KUc6gv5JxXGcezKIpi6EoTDiCTd5MsQ/HoWTUSx07XHh
cS8/6aUGFYc0KGAQdp15NCRkofkdTg7xfX7ergEeLYjYhbuDBr18xITGItxY
lAsYoVNBwwKwUhJV2CqHFgmyy0F/IK4nJLKbOEkTbCphWsuAtJFou7GR5kEF
p5NxWhnRyLHZwLvcSWZLQncH31yNm6uwuJmoJVjSKszP3DwPrpwUmk3cvgop
hpI2+ile0kyUYk4mSbx0Dp46CIuuwMaquI4mXtrByzpj7eb4sDflwPH3X/5y
3xvfbHttuZD+/rJ808vLN76yfNOrX22eYnDzy18KXvR/P13zu8Urnv/gs9lv
Lnrur+/m/emv2b/7Y+bzL2Y8OycuMTEhNTUtI326EAmz5uROeyF3isGcac9P
y56bnUFrTmbacxkpU5X6XGby7Ixk6kvnUH1MS3/ntcTTBamXr8dev8EXlyWW
FItul5CyMny7jC8rF1WW4cpyrqIqsbYpoalR1NyIWltQWyvu7IwVttB0c1Ip
L+lCUimWq0RKTZxSE6vWJ6gNcTpzst6aZjAnmSzxJhOxmoVjvy4bcdsgpS/o
4nx27HcI10AFnNhnhz478VpFAQdxW6kCEsqjtgNf3oOOfR/TfBmra4C2Dmkb
gKER2Ts5Qwurb4SKClZ+B2kboV0K7Uqi6wQmMXbIsaUTuLoEAP1KKoLIT/Hs
ZP10ZDagXuqEZTSVUAZBqFswov0KIkQqOeqV4kgnG6xHNAkay2H3DVi6V2BK
cYHtymc78xnpOdjwIys9wcqvgxs/MRWnQXNhjLwY1B0HVfug9JwwW1J7kG04
zCguCYsmjiZcdzamtZCV3QSKImAoh4bbrE14HwSpE5ZgirC0AFlvsb5K7K8B
fW14RIImtfChkfS0oEAjCjSBnk5EhwVLGdSVCnO/badw8UamfCdzZ39MxY9M
+R6m4SjbUcCYG3CPEfZZiU8paP2oAw/bQb+B9Grw/QD3IILG3cI+6qgCD9nQ
kyHuyQj/YIDCSP41if5zL/bfk6JfhxFVw6dD5B9jFEz+11Hu0SAZ8/N3gzRL
kgk/fjpG7g/CiTAZ8XJC6zofeRAlk2FMpS1kJV499mqR34iiLnR3OC7oJjYl
dmkRjRX9Htzr4EIUwyg/FMSUTYeKmLtZSxe2SpFFAsxdVDfhQIgf6o/tjSRY
TXxnvdDdrLkEylp4SqJWgnQyYQOMVs5p5cRmSXQ60w36pPYWrqpUWDqUNAv9
oFtrYPlVePkUvHCUvZrPVpfy4kaslYkU7XFyMd/ZFpt/BB7ew1w9D1qqRZI2
vqsxTtpGwY+3mmd8te3rP3+x89WvtlD0Xv5y6/9+temVrzZS+ug7f/1q28tf
bv7zFxv+9Nnqlz78cs47Hz/z+vwZL7+e84c/Zb7w+7TZ89KenR2flJhMZTAj
Y3oWjYQZs3OyplwoBVBgcHZWxpysKQbTU4VKS5mdLvjS57JTZ2Ym/uGZ5L0H
kguvxF+6Gnf9VlxRSWxxCUWPLy1Ft0u48lKupHTKnVbH1dTFNtVzjfWouQm3
t/FtbaSzkxN3YnEHEncSiTxOooyTq+MU2jilNkltSNca07TGZJ0xVmfARhO2
W2NtdLR04AD1nE7steOAG4e9wiELn4N4bchLxdHGucycywS9ZtRZzp/bCQ6t
Yq/sArIKqK4h+iZW10gljzO1Qn0LUtUgaRmrrkXGDuCko2UX0rYjSxe0Ut/S
SaWQhj4UVGGKnkOKaOgI6fheC/LTJCIFASUJylCQ+k8V1yvHvXKhdUWkW2jy
663BuiJWfwfW5ccU7WBaT0F5AWw7zXSdY6XnYe0+Rn4SdF5mr/7EVJ4FLYWM
ohRUHWYbj6DOfLbqAFN1gK0/zMguAms1NNXBqvyYlkuspIgyCHVlrKGMtdYI
W1j9nTikwB1XGelFaL0N3Hdo6APhJjzcTUbk8IGRG1PwoTYY7kCRNhhpwebb
QFUMDBVAU4KKNzMlWwQRrDzIlu+PqTrINJ6m/wRra4O9VtxrwREq9xY07uXG
XLhPTx0pfz9IHkSExsd+6sAVeNiNnwzHPhkljwbxP8a5f97l/30fU/l7Ooyf
jqBfxtA/7+J/3+V+HoaPBrlximEEjwfgRJB7Msrd7UOTEX40gId99FPkcR83
4iUuBQxaKVycRyP0kgg74dhgvM9KzFJgV+CAGfX7hJUmnw4Ph4XrLp06aFUC
+sMydUAjHTklyCCGLg0eDIgGw6KBaGxfNNbrjFVJSUsFrL0hbBmVNiONhFd0
YRXlUSXcbq3X8SZzksGYKulMrCpBVcKKIS9uEe7bLCpA+YeY0wfAxdOwrpKT
imPVMpFaIupo4q6eQz9ugflH2MoSamhF0jauu4k3aRNN6tnf7/zkL19u+8vX
G17+asMrXwkW9NVvtr66YstrX297/asdL3+x8U+ffPfS+8ue+/vCGX95Y/of
/pz1wh/S57yY9uzc9GfnxiUlURnMSsukOjgrO+PZaVlzpk97PmeqpmVTACmG
z2WkPZue+mxaCmVQMKVZSc9mpc5MSfni0+QzBUmFl+KuXE+4ciP2ZpGotFRU
UsIVF+HSIv7WDXKjOK70TnxlJV9XFVtXhRvquaZmvrmFtLWTtjbc2UbEHVxn
t0gsi5coEmSqeLk6QalLU2hT1PpkDQ3ROmw0cyYjMf//ns47PIrrfveaU2Zm
m3qh2NiAaaKDE9tJfi5gUJcQIIzt+OduML2D6EVCIKHee1lptUXavqtt6hUh
ISTUKyqAHSdxnOTev+93SJ4L59lndjSClWY+533fU5uFsdz9vaLHD9lXc37F
T3rZ3g7c1yXq6YIvQTwEANlHrbinndWWcnePoqvf4puHGEUSsctRgwo75aRd
z7bpCTBYr6SWUmKroA1q1Gkn7Q7qrCUNOqhdabsRSKQPQewc9ImL9jq4djPu
c0EMFJZu67LwvXba7xD2KBmwkLF6CEpk3MlBKhwwkacG2llKwNrZCnDBJSbv
JDIkYksS1sQxlhRkSWIqzzG2OKpJQWlXmMokVJuK7EWo9BKqvQ0Fl4AwXUTy
K8j8ALWVk4ZyWhLPaNMxMGjNwQ0Cg7hNjjvV+ImRQnwz5SJTCm4vxg/LBO/a
V4knhCGj7Hw9+6KFH7XgYTMwiAc1QvuMIw9qBtxWhatu4MzvSfEZVBbLlN9A
xVfc5OCKk5CrjH1oRhOPwPgJ226CY3wxIJrpZocc3GgTeTnEvRzmxlu4XiMa
bOCfPeb+9kz0C2TDae4f86J/Pqf/fu7+25z4H3Psr8/Ib5ATX3L/WuD+OkOf
j4hmnuDnw4LwvRznf3kmnh/BC2Pc1BPy7Ilk4Sn9yzj7tJk+cqH+NvEjF3no
5HuaucFePDvp2QPVr+XVKtmt4vE+0t+K+5rws1FhJmmHi7ZZ2FYzbTSgBiNp
NPPNRvy4iYKPHRmSjgzTcfi0g+4DfdJWJ6evJPIMVJVNdKBfGolVJ4G45wSs
bOIGh6ytTdLa7qXTeIEFLc2iGrmoppqW5JGkW+jGeSbuCspOZqvLqcMicll4
i54UZvCxJ9CtiyQ/k9VrJCad1KDk2+zeBmPgri+PvPPZlbe/OP7en4/+6fPT
f/zizB++OPunz8/94ZMT2/d+vzn887U7Ipf/Ycey7e8uXb9l0erAgJVrA1au
WbRyjdA34eWz+D8MLgIGA1a9tvg/AK4BHoHBAL//z+ByP68V/p4rAzxW+npu
We554ZLn3QeylHR3YWuJTIHBAkAvi8/LkWRliFIzJXlF7iVl4opysbyUq5Jz
SqVYrRbV1PAaDQFHqtdKDEaZ3iI11knNNrHVIatzetc5feyN7naXxFHPN7fw
LY1sezNwJ+p9yEES7OkUpLD3odA40yv4T/L41aSnh21sTzt91Mpqirn4M+jy
D+j6ISblHNYXYGc1tVeS5hoQQdKiJU0aoBKbSrFTwbYZ2U4HdRmprRY3QXyw
CAB2WshDmxD/heBvEfbx6a/nhttJTz3ttArbTT4BDK10sI6OOOmQnYw6ueE6
ts9AnuhoUz5yFtKaFLeME7jgNDImMfoEBoKbLYOYEhn5OTfLHaJIRClXGUUy
MIhtxaj4PNbFMaqbuAQy2kVUcRm+C7WUEWshLrmLtRnIkoct2aixVBCylgrU
ocJPzEKSMhdhYwoS2ltKUG8l6SlDY0Zh3dQZO3nZyk456KiZDOpwfw15WEns
+dhVhDuUUD+Q9O9QwQkGvGjFLaF5tuQ6o7iLDdkI7Ppjl7Dd1UgHO9nNzfdx
c0/oTDd9WscDjD+N0edPucF61GMhwy0UbOTf5sQ/TdC/znC/zov+Nb/k/7zw
+scc988F/rd5EEf+/76U/DYv+XmGPnvKzg7QhWEyO8D9Mi15Oc3OjpK5UXay
j3v2lHs5Cpyy3TbS00get9D2OtA4treZjA1wzybcHzaRRiPusnH9bcIKCT0Q
DVq5qVFxf7eozY6aLaTZTF064jSQZgvfYsaQQYb6+KF+0cSgZHxIPCpMxZWM
DMm62/m6WlqVj8szSFW+WCOXaBUicw3vNIvsFlG9U9zW5t7Y4KGUi3NSSUk2
kMhWl7G5aSThJrp6hrl1ERVk0Dq9zGGQWmtJaS5/+SS5cgqnJ3I6pbuhxrNW
KXXW+Z++GPKH6OPvfHriT5+f+vCzix98cfnDL2+8/+fY38cc3bb3u41hn635
KPyNd/7ntU1vL127AegLWCGURStX+Xp4+np5L/L1f93f703/gJWLA94C9JYu
htc1ixethjC4yA8y4Ap/jxV+niv8JG/6ei73d1/uJdsb7B933yMxWZKcKktJ
k2RkSTKzRNkZbE6mKCOFT07mM3LccwtFJSWismJRRZm4qlKsUIjVKpFaSdUq
VlMj0ho8tEYPvVlmtEpNdWKLzdNi87E5PWwukaNe5mqUNDRQUMBuYcwM19Um
jCB93MO/apYh3Z1cd7uwNmnPQ9oNbzu4dhdfkUlun2auHkHXjqJbP6LieFwn
x45q6qzGXWYORLBFB8fUXIosFdiloZ2QDpycTYtdetpqZsHSgMOBePjIScEX
ddtpm1FYQG+gmR1sE3dY0cM6/MQpJMQnVjICCdFFhuFRd7CDrxh8pGbs2cic
R0pvMik/CgKnu8eobjOae8iRRQz3kPy8my6elN0jaVeZqhRcm41N+UxJrMz4
wLvqqlthLCm4gORXkf4+01iGdfmo5C6pzUKWfGzKBAZJSzluqMAdKtJvokMN
tK4MGdNxRzlpK0aPqkCC8aCOnbCRSSt53szNNtARGx000YFa0qMmrnxsy8Mt
Cq5dwxVeRpnfMGUXmArwVHGAoZsiHqkhXRayzRpm7CE38Yid6KYzQl85NzdA
J7uEGbgL/dzLMTLbJ4xa6TELe8E/H+P/Mi1+OSn66zPATfavBQmU3+a5fzwX
/bbA/58X/L9fSv7yjHsxJZ4ZwPPDQmff/BD/11l2YZzOT/CzI5LpJ/zCMPfz
JDfdy3Va8aNmvruJNJlJh53rbWXHn4qmR2WtLg7uTruN9rXSoU6+w4z6Wvix
p+LeDtJsBfRIkwnbNNhhoI1W2mYlgw8lg0/YwSd05Kl0eFAyMigZHXQfH5GN
DPH9fVybS6SpEPbVrchmK6HkUk0Zb6mROEygiZLWZnenzauiWJSfwRZlsaW5
XHEuTUvEIIgXjzGZd/naKomlljeqRVVFfNxV7sIxnBLHqRQeeqWHUS2rKlu5
M+bT3+879McDx//n4PH3P73w/qex7x089XbMj0L/YPQ320M/Xf3eztc2bluy
ZsOiFWsDVqz1X7HGH2D09Frk5bvUx3+Zn/+bfgGCFC4OWPWKwdWLBR1cCTlx
kY/AoI/7Cl+PN/1ky7w8NyzzPHvBNz5RlPhAlpgIDErT00TpKWx2OpuWzN5P
oMmpkoxsPq8IIiFbUsxXlPMKuUipEKuqeAiG6hqRSivRGtz1BhF4UYPJU2f2
Nlp9zFYPq11sr4dsKHY6SWsz2wFetIG2NwOAfHcX+7BdwO1hK9vZ8p9Zh2wX
BMB2rt7EZcSjGydw7I/o2nEBw3tnGF0+a69CNgUEB15woQZSryEmeHRLmToF
brFwHS7SaKG2GhBBrskopEKwo13wjDWwD8Ht1BGI/H31/CDETBdtNdEeh7Dz
ch/ooJ2ONYsGnWTYSYedQjzsNaAmSPdZSJOO088wyYfd5Ddw1U1GfpPRJiFH
JqmJQ2VnkfI2zY/DmdeZ6jRckwcM4qJLYl2CR0WsW/4lnH8BVVzDmrturnKs
K8RF8UibzVgKqTELu0owmEkXEAcMmulIM+tSEEMG6pDTthLUVUnby3CPkoxa
hF2Gn9XT5y3cJHw2C9unwb21bGMZMWchVymF3GcpJMlfoYKTTPk1t8oEVBGP
ym8zqiSqSWXqSlGHCY/3iCcek6nH3EwfNz/IzvbT0VY62EBfjHA/TWAwor11
uMdCRzu4nyb5n59JX06K/zYr+XVe/K8F6T8XxL/O878+5//5gv+/P0l/ey7+
aZqFCyb7ydwQnR2kz8fYvzzjnw2ThQl+boSDbPhijAKGo91cO2DYxD5spqB9
7U72UTM72s+PjUgb67BDi5stbE8r6e/kG3W4y4WH+8QPm0mjCTcIUkjNKsam
A1NKmuskDp1nT6tspF808hQ0UTz4RDY8JBkf8xwflk0Oi8eeyvoeitob+Loa
Tp7L5d5HGXdQXhKpKmT1SrHTInE5pDarl7rKA1xoWgLNz+BK8qQpCez5Y26X
j+PMBFZZyuoU4poKvjhLcu0ce+k0zksR15R7Oa2+N69u2hzyv29HfLE98rO3
93z99t7vtkd/vS3qq7f3fvvHA0fejfwq8P2Q5W//admWd15fv3np6nWL3lod
sGKlt7tngJfPEi+/1/z8gMEVAoP+by0JeGvpKx0U5vD6Lofi7/2mj/ubPh7L
/GSvu3u8/zvP6/HSu/fFCfdFifelqcmStGQ+7QGX+oBLvMc9eCBLSwdrKsrN
5fPy2CKQwjJRZYWoqoJTVAqOVFUjVeukOr1Ub3Cv0UlrDd56s7fWJDPb3K0O
idlGbS62qYlra2IbXbi1ievqEHe0sZ3CqqRcZwvXAeLYJuhgRwvtbIVfHZt4
FV8/43bpmNuV48z1E8zVw0zRPVQnJ8CaS0VbDbQFUoOB1lVhQzE2y0m9Fnc6
aatTWGTSpaVNJtpkpk1G0gpGtJ7tgmDiYltMQnPNk0ba3yw8Hu117GMX3+ek
j+vQ0wZuuJEbAil0kiEn+9hCH+mxPZuac1F5Ako6glKPMxW3UclVVCb0AyJL
GlbcZApPk7KrJOM2gqLMIJocbC1hi68IXYTlV9zyYpm880zZNaxMYBwVpKYA
FSdgfS5jKiT6TOQsw43lxFmKW5XC7mDDrcLW6sZspr2KdpSjzgraIRdacgYN
7LhVWCpwoYWbasCjNoHBbg3bXIXMObiuEAPCLRqSd5FJ/x6VXXWTx0NkRhV3
UVUCUqdgbSbjkBMwAJN9kqknwt5zc4N0YYgCj/0uOt7B/zQO1pFOdHM9Vtxj
IxO97Isp6ctnkp+mJH+fl/06BxjK/rEg+XWB+/UF/6+X4n//LPtllvtpmpsb
FU0PsPOj7OwwfTnJvpjkZwbRwjg/O8TOPKUvximkxb4GrsGAHzZznU2sU0/a
XfhhIx0RJshI6kHsanGjhfS1sz0tvEMNtHJPH4la7Mihx+BF62qwUYlADVud
/IMHq7+5EJyZt7rB5jvQw08BjP380FN2fFg6IWAomhjhwaY+7RH3dPKtTpG1
VlKZR9LjmaTrOD2eyvN4fZXIYZI5TJ5VxZLM+2xqHJ+dTADGB7fotZP4xhku
/TZfksrJ80WVuZL0O9zVk8z9q7K8rGVnT7+zafeejWFRW8IPbIo4uDnq800R
n22K+BQOtkZ9tSXss7UfRa7+IHTl/wSteG/Hm9v/uGzz719fv9Xb3cPf02ux
j89Sf783/PyXB/gLraNLFv1XB4HHAL+V/r7LA3yW+Xi84ev+uo/sNal7VJjH
nXuyu/dk8XfZxERxahIAyKY/4BPucncTRMkp7mkZfFamCNxpbh7/ikFJWSlf
WcZXVYmqNTJNrbtGK9UBgFpflTagVgBQYrS5G20yg4Wzu1hXI1fvovV22lLP
trfQpibSBri1s60NpKWeAIMdLaSjlbY1iOUF9NYl5uo5dPkEA9XU9ZNM7GG3
u6dQbSGxKbBVQZr1pFmHm02cHW5TKWMopxYF22xGXQ203sJaa3G9gUKub7Kw
wGCblQoMNpB2u6CJjxvZJ81gRyH+4y6n0JXf5+D67HikRQSJbNAJdpQOuthH
Jq5Dgy0ZyJSH866ju9+5ZZ9HxddRwSVcfoupTca6ZFx+HeWewrmXUMotlBGH
lJlEk42txbTsutBFWHaFybvMZJ9zK76KFHdRXTlR5jHF97AhnzEXUm0mcgit
NJAfSbMC91tZSGQtetaUj1orSWclai+nHVWopRT31bIgheN2PNtMZxqBQdpX
S7pUpFWJ6gpYYy6qryAderY2D6V+j4tjUcVtYJCpAgzj3VQPsCYdGQuxS4ng
B58aEBic6afPh0Wzg+xYN//Ewc70cC/H2flhCpnxoZUMNIumBriXz0Qvp2U/
z0j/Nif5x5z4nwvS3+ZFf1+Awv37Z4/fXrj/PM29nJZM9oP/pAvj7PNx+tMM
NzvKzQyxC2PcsyExkPhynE71ce02CHeoq0XUWMfataTNibsaMCS7wV6ZrRbZ
aki7jYXQ11XPO2vxoxbucRfrMgn7pzsN1KREBiVqspN6p+zwhfffPXgo4rvo
I2ffSbi/rrJiiVXv2dYgedrNjT9lp4bEM6OSZ2Ps5BA38oQf7BE97pK0NIrN
Oq6ygMu5T1Pv4Iy7tCCVrSwStu8szubS4sn9ayThOnv/Jnf/Gr11EUIiibtA
b1yUXLzgf/LI8qiD294NDdoYGrNu9971oTEbwvZtjIjZHPnpxohP1oXuXRuy
f23Q/nVB+9bu3rsueP+a3XtXfbx31YdRaz4IX/t+mJ9U5u/pucjba6mP33/t
aID/qsWLoAgwCo2i/it9fZb7eL7pDcX9dS/ZCl/vQz94x92TxN8V303gE5Ok
KYmitCQ+KUF0+w53P0mSnCJOTeXS0jggMTtfXFwkKiviQArLyyUKhVSpktbW
eqhr3ZU1XtW1fiqDf43RQ2uW6U1gSqnNztlcXB1IoZUKE53qSVM9bm6kLU1s
g4M2gkFtJC2NpL2RdZhIdgp75Rxz9Sy6fArFnkBXTjFXjqJL3zH5ccSsIOZK
7FATqFoBrnrwYAqsK0EmBYX4IMz6dLLgXhxCoscNJrbBIAR8EDth8wIXC1Uu
SGFvI3nSwrXX0Q4r6XFyPQ7SY6dP6/8zp4YdrGcH6km/U5jlVF+ODZm4OgWn
nEN3DzF5V5nsSzjnAq6446Z5gFWJuOgqTjvOpF/CSTdIdhypziaaXGooIqVX
mOpbqOgayollMi+4FV0HScLAYGUWU5pETEUCgzUZoIy4oQqDjXTJcZ+VjrXw
bSZiLmRaQAdVuLWcdClJQzHTWUX6DXjMzs40CBMfxuzkiYF2VONODQH6tOnY
VkJaammznubF4qwjwCBRPGCqU3FVElMJ6TUdqbOQoRg1aPBAGzszwE8DOAPc
82EO1Gq0k3viorP9/MtxDqgZbIPITAY7+amn7Itp6fMpycsZyV/npL/Nyf65
4Amy+Nc5CIbSf//k9fd595fT3MKEaPopfj7BP59kf5riFiAGDhPAcHaMnxvn
Z0bo/Ag30sVBygNpa2ugThO164WZR+0NdHhQ/LhbZK0hVjXEQNTbJmqyEHsN
6m5mu1pYaw2uq0FwMUihSYXb6qlFK9v3/a7t+w5uj/xkc3jMO1EROw6ERn+1
45sTfzx/6+2bCVuTU1aXFLxmUPu1unwGut2FXv5+8cAjruehuLNd0uDgjTWs
Wk7lBWxpFinJwUW5NCeD5D0gSTfZUyfcv/x22Z7PNn0U/c47oX/c+PGO1R9H
rNm1J3BnxOodoat3h68Ljl4fum99WMzGsJjAoOhVH4ev2RG55uM9gUH71wfB
mf1rgvatCd4fGBKzMSRmU/hBX6mHr6eXn5cPRMLXff2EpS1A+BYFAIMrXzG4
yt9/ha/PCl+v5d4eb3qDEfXZts7z0lWvW3HiW7f5hARxYgKffF+UlMDfuknv
wtv7kgeCMopSH/AZaXxujrggjy8pFhWViUqrZJXVsmqVVKGWVCm9lBp/JcCo
k9XqPXVazmQS2eziOhscUKuVs9n5OgfrcJLmBr7RyTksbL0NRBA3uUiDnSrK
ISmTC6eY2HPMhZPMueNul08K271d+gFdO8yoC6lJgU1yWq9l6/VCTKjTMPoy
bJRTsxIyIIHb6jASWy3vMrAuI2kwsuBUW82kzSbskPWqwY1017MQ/x+6uBYT
hET+kYM+dtFeOxluk0A4GmxgnzbQfifpBUK1rDEb12TQvFtM/BEm6TgwiNLO
MTmxSJ7gVn0fVSbg3Mso4Xt0/wyTeF1SkChVZCF1DtblM0UgRtfdCm8wWbEo
47xb0Q0kv49MFbg0lSlPJdYyZC4iNemMHXSwGpsKkL0c99axY+082GZTMdOs
IF01bEsF6VQTVzHTVIq71XjEwo7byLNmbsxJBiD2KinIdLuWqJJBqVlnJeq0
s7oifO8LUnwFV95DwKAqHVcluylS3NRZVJ3FGIpwo46M9vIzQ6B0eH6IXxhm
nz0VOmjAnM8OiZ5P0mdDYBLYbgcWMBzkXs6IFyalP027A4Z/n/f49bnn3+ak
f3sm+udz2T9/8vx5TvzyGTs/wc8M0xfT3PMpCtfPj7PTwxQQnhsTAYZzI3Ru
kO9rpS4TsWnZ1nrqNGKbDjfYaKONAIZ9XVJjNTJV03oT6WpkXTpcp0GdTTxw
alAwZhVrN1BDJQEMO5tRft7r74bv2rI36p39MX/85MB7B79895Ovt+77fFPk
ARCpwJCIwNCgDZFBH8QE//mHd27FrZWXvmEz+7S7JN3N7r2dEmFBlS5ZR7us
vVXW0Sxpcbk7jT4FaX6ffLJ6/Ud/eOuDD1e+H7ry/V2rd+xevQu427l6x841
H+xa89HudbvC1+2KWheyb11ozNrd0Wt2Rq3cEb7yo/CVOyLhbeArKVwbDB9g
/7rQ/evDPln/ikEvGWDovdjHV1i0ydd/mZ8vMPjWq2AIDK4I8H0Tir/3MmFd
Q48lMs+Qnd4378hu3BbdvCW+e0eUGE8f3GPv3MQ3bvEJ96UJCfz9e6Kke6IH
D8Tp6aLsbFFBoaQAGCyXlFfKqhTSyiqPskpfudq3usZdqfVQ1Ui0tazZwlvr
xCYjZzRQi01UZxeZrdQmDCLlHXWkzkJsdbTBiUAHrSZpejI9dZKcOo1iz6Hz
p5hzJ9wunQYv6hZ7mDn7tVvKFWysxIZKZK0m9bUEgp5NS4wKoi3DAKC9hoAC
wm21agURdBnZejMLTqbeSFttbIudtDpELh1qrSPdDbSvWQyPeouV7bILDeO9
DnYAMmAL399IBwBAF33s4LrMbH0V1aTjigc47RITfxjoc0s/i1POMPk3EKQt
eQJTGoezLjI3v8R3z6K7l0jeXarIRiCFNXkk/xIpuc7kXXfLuMQAg4U3UMUD
ZKwkRcmoPB3bK5GlhKrTkbUU11cTYz6ylJGHVrCCXJuNtZSh5mrcBY9rJe7S
EGcJ4yjGbQryRE+HzGSynh934kEH262jHTW0y4gNeaDUxFyC2oxsqwVnncXp
R3BlAlIkY1Um1Amo6oGbMgPV5CNVFmMqQx11dPyJZHpIWOZ6fpibG+FmBtkn
TeyTFjw/Kn4+ISzlCl4dfjPDD7nZEfHLGa+FSfeXMx6/zEI29Ph1wfOvs9K/
zUr/8cLj7889X85wP81KZkfZOQiV0+zzSSCRfyYsmi2U2VH+2Sj7bJiM9Qit
YVYASo9aXNSmxzYDcZo4MJlDA7LOFrFBgeDmNlrYNhdrrgEjStoaWIeBaCsY
k4ZYTFxNFTXVsk0O0dlLK7aFh7/3Sdh7Bz/5w8GDf4j57N29B7fvjdwcFbop
InRLVPiWqLDNe6LWh4Mw7V2/a8d7we+ExWz6+vs1588uu317yYPEgJzUxZkP
lsbHLT51bsXeg+u3fvDeyj9+vOaDoLUfBb/10fsrP9q5bmdI4I7gDTv3rPsQ
dDBy8+7oTUH7AoP2CgwCZXCwK3rVrqgVOyNW7AxftSty9a7o1bv2wH/3isGY
wMiDGyP/7Clx95J5+nl4LfYGKfR+zcf3dV9IfwErFgWAF10pMOj3ikGf1308
l3p7LPVy//JLr1u3pddv8DeAwXhxUjyXcIe9eo27fdczPgEMKpdwT3T/vjg5
WZKeJs7OkWQXSPNLpMVl0ooKWVm5rLjcq0K5WK72UKhlCpW0ppY3mTiTmdfp
qF7Hmc0So5kzWUidjdhsnBXcvhEYFNmdrKOO1VRzd26x3x/BJ47js2fczp5m
zhxnLp5Gl04yF4+6nf+eiT2ESlOIUY4Ncgy4ObUI8oJZTWtKsa4Sm1SkycqB
V7Gb2ToBQAxq6AKILByQ2GLnWpxcg5mrN5JOB+5tEXouGo20xcx12XBvPe22
kcEm7mkT298ADJLHTtJtpR1GFqxjVTLOuemWdAbHHWJSL5D4wyTxFFMYx8Dj
XRbHFNxCaeeZSwdJ/Hl09zLKvcsosokikyhzSe4lUnwD5VxjMmNR+nmm4Doq
f8AY5CT/AVORiewKATpFKjGVYKeC6PORqYR0WsjoQw4Sq6UCN1WTLj3bUgVu
k3WUMpYC1CgnD2vwExMRBmC7yFA97TGSVjXtNBNnJSlLQNp84lKRniZeV0ge
fIkrbuHqZKzOhASNVVlYkcKos5EmlwCStmqhfXhqUAJSNTMonh8TzY/hyT5x
bwMaaOMAw4VxYeWQvhYIznj8MUQ86Ytpz4VJr59m3H955v73eZBCz19mpH+f
8/jHc7+/zHu+mOGhPBsBKRQtTLLzk9yc0EnBTQ/RmWFgkH82TGefsr3gUnTY
WAUYkiY7NWtxnR7B/WqEKmXQo6NJoq0gBgVurKMuKwHuAMBmB2fWMOoyxqKn
Vh1Xq2TsJmS3SL48um1r1MG3Y/Zuj47csmfflujgrVFhWyKCN0cEbYkI2Ry+
a3N4yJbIqE0REWt3B7/14c43/vT+63/44M0/7Fj9p48D398V+NGOdR98GAjl
o7DAnXvW74rasAtojVj7ccTanREbdoVt/Dh0/c7IwI+j130cuWn33m0hn2yC
3LdLULq1ISB2BwKDY1bvgvS3Z/VuoC9q1auyVoAUGDywIerzjVH/6y6SeUk9
fNw9/T29l3h7gxS+JjjSgDcWLVr+qtd+hT/ooB8wuMzXa4mHe+CbnifOeFy9
Jrp6mb15i78bzyfcZq9dIdduSm7HS+/EcfF3RXfvie7dF3QwLV2akSPJzJPm
FbsXlYoLS6Qlcr+SKp8yhUxeLVYoZRqtRGfgtDoqDJsxiYwWsV6YWMFaLMRi
xCa4EXrOXMc77USn5BPj2OPHuK8PsT8ewydOoZOnmFMnmHOnwIu6nT/GnAUR
/A7du4DVhURfjs3VQlsZ3ERrLdbLSU0J1ldBjco1u7hGB7HqhOH0TjNxGKnL
LCyf1WglzXa22cYJNxSEz0keNfKN8CU9aTXSHid9BGccdKCZ629gn9SzwlQa
G+0w0WYt1WTRgjiUcpGJO4runUD3TuGr36P4Y0z+bUaeSMBnZl9j7h7Bp/ej
Oxfc7lx2y7rHVGYTZQ6WZ6LM87jwJsq5wWReRmkXmPxbuCKFgWcsO4lR5CCX
ClvkSJ4sdKnYFVRbgMAltpuFGeidTmqtog3VpENHW5WoTc06y7Exl7GXYDCo
D/V4wErG6oX93CGxtmpIoxq3GrhyMMZpyFyJuoTmX1p2lWQdw4okIQlqcpC+
lKqzsTJN8MmaPKAS2VW0p5GbespPDgi+FMRrbhS44x830acddGFMAjZyYoAf
aKMDHXS0l50Zljyf9FyYcH/xzB1I/Ouc919nvf4yA4Lo9dcF77/MyV7MAH2i
uTEBw7kJdmEKXCgHkRDU9tmQIKYzI/DviyAdmDVYW0XArjhtxGLA5lpsqQUD
ww/0SzpaWG0l0cqhCqVQRZs1COTSaeYMKqIuQUYVMdUQvQo7TLyuRrbn69+t
DQ7fFLFzW1jElrDdG0N3bQwD9II3hYZtDA3fFBa1JWL/lvD9m0IiNgaFb9od
vnl35Oag6K3B+7YG798W8t+yPQT42rc1ZP9W4fXApuD9UDaHHti0e9+GXfvW
AoM792zevX9zUMz63fsCX7lNQeZCD6wN3r8GkARxDI5ZF3JgbZDQIANvgdC1
kAcjv9i850tPYFDi7in18PMEKfRa8l8p9HsjIODNVwq43N/3DT/vN3wFHVws
8fjgXc+Ll90vxbJXYtm426KEO9yt63zsFe7GbQnEw1txojt3xXHxPDCYnOye
kiZLz5bmFkrziyTZeT75pb7Fle4lFZKScq6yWlSjk9TqeJUaqzVE6CU0i3RG
VqenBj3Va7GhlhqNtM7Muqw0L4X7LIr/7Cvui8OS73/kjhzHx06QYyfQaQDw
FHP+hLDj8JkfMOhgbgLRgORVCBsN1IHbBKKVBERQW04hJjTY2EYnb4Wq0oDr
razDBNGDbbDyLgtusgnzrOtNrNOEW2xCgwyQCAA2GYWBwb0uvqsOgQ3ra6CP
62mvE7IhnKFtRqEHpCRBGH4WfxLdPMwknSO3j7td+c7t9lEm8xqTfwdlXmFS
LzFXvsRH9zE3L0huX5KkJ6DyTKLIxsUPUMpZknOTybrJZFzFcFnubVSRjmoq
cWYSU51LmmqItRJVpCBjOWOvprX5SF8sdKAMdnGdLtZajRtUtNPAtgJfapA5
qgUPWShkxmY1fmQkg3Z2qIkOtrFdZupSkBYjrcnD+XFu2lLaZEGP2yX1apL2
I5bHMcpUrMykumLAkKhysCKV0eRiVT7SFrFODX3SwU49FY8/AQmD0Aevwg62
PU14+BELuM2NiQHD/g46+FBY1gwwnJ/wnB13fz7l8dO01y+zfr/M+QCPf5nx
/tu8789zHgvTkmdjFNB7MSWen+Sfz0hmAcNx0StTKpoc5aeH+Z4WDqKfQcmr
K7DVQOpB5nTIWEsMagI37umAuKVerClnaiqQpZZatAjU0KwBBaQ1cqIqZgzg
21XUqAIXROWFPu9G/ml9WMzWiL0bwyI3he3eHBq6JTRiU0jk5pC9W0L3bxVK
zPaQmO3BMW+HHHg79MC2UOAuZntozLawA9vDDrwd9sn20ANwwbawmC1h+7eE
xmwNObgl9NMt4Z9tDhWEb0Ow4GYDd0evD4oOFEJfdKDQJrN/XQjACM4zcm0I
nAEkPwkM+QSoXLt73+rde1fDt4QdXB/+mbtY5imR+YEOengu8vYEBpcCbsCg
v/8r+fNd7uf7hq83YPi6r8dSd8/ocM+Ll/jz57krV8VxdyRxN0VXYvkr18U3
bolu3ORv3pHcuMPfERgUJybJktPc03Pcs3JlaRmynGLf/HLPglJxcSlfWS1R
aSXqGl6ppJoaXmeQ6vR8TS2tqSFQhJFsWs5g5OqsrEbOnf5f0foA8epl4oNf
yb48Qr79kT10Ah86io8dQ2dOoLPH3M4ddTv3I3P6e+bqSaY0HcMteGU7kdPM
WmqxtpLRlIERJTadMJPabiF6DbWbqEMoQJwgiIA5GJvGOpFTz8JBqx13OlmX
kdYb2CYj22FD3Xb2oQ1Dbf+4nu1xCePWQBM7zKSpFiuSSc4tJv4Mc+NHfOMH
t8Tz+PoRtyuHmbgTTPplAcPkC25JZ5kzB9CPMUzsGcnNi5K0BFSSTuWZJP8e
k3SGZN5kMm8jYDA9FgGDII41cpSRhKqAQS2yViF5KjbKUV0VqclltEWk2QKi
w3bWs2YlrtcIWtxWS5pV2AWxNJPR5SJTMQLj2l5LH5ton5MMdYke14MOQjrG
dg3JvYWqc2mdBve0ih61UsU9XHABqdJwtRAJGVMVri1llJlYmc6Ao1AXIGMF
ajKR4V7x5CA/1s+D4VyYkE0PcUM93MNG0D5wpNLZMfHYgGigCw918yO9/OyY
x7MJr5kx2QsBQ89fZn3/MuP7cgpI9P1l3u+nZx6A3vQwOz8hgki4AMo4LZ4d
h2womuwXdgyZGRWNPhE1mnBtOaqtoIoibIHA7qRGHdEq4Ybiegvf91ja4OSU
ZVhTigwqZIRqXIkNSqRTYnWZsIyhrgrrldhUQ50WcvHaqt8FxWyN+mRrBDC1
d1vo3q0h0ZuDQrbsCtm6G16Dt3wMB5HbgqK2hezZFrRna9CebcHRW+Ca0H1b
w/YDjG8DpKHA3f5Nofs2CScPbAk7sCn8wMbITzdHfLYl7NN1IHzB0f8tIdHr
wvauCd2zNjRyTUjE6pDwtaHRa0OFRpg1IftWB0evCY5etXvPKnCnIIihB2Qe
nh6eXt5e3r5e3v4+Xot9vF5h6LvMz/8NYVV732WQBAFAH6/XvT3f8PH882fu
p87xZ89w165Jbt/kblyTAJJXr4uuXueu3RRdvyW+cVt0C+xoouResjQ1wyMt
0/1Bqiw91yunRJJXIikolZQrJCq1e7VKpFTRWp1Yp5fU1HBqNalRsbVqVFvD
6nW80Uxra7k7lyR/WsctEvH+7txSLy4kVPTNj+KvD0u/PY4PHWFOnECnjqPT
R5gzR5hTh93OHcYJl1FFDlIU45pybKolNhMFc1JThmoqWL0KWMONDtagJYZa
1mYQZlLDBZAE7SCFNq7JxrrMnNPINkHEc3KtDpHdQKAWbTSBZ2PbrQjyYF8j
7alnH4EI1nOdVvCoxFBMc26i1BvM9SPo2ncItO/OaQQAXj/C3D3DpF1mHlxg
Es643T2OjuxFP/6ZuXAcXb+I0+6RwjRcls5kx+HEMzgdjOgdlHxVEFMApCIb
qSpRehJWFeFmEzFXYXk6NlRiqwJDRlMXCNLc18J1NFKzmrhqhKqgTU8aVcRV
TZQZjCYH6woYawUF6Dq1pEMvNJgMdYhaTcimJPVGWpGKShKJrhy3OYVFkJr1
bO5ZokyCSIhV2UhXjswqXFNMlFlIBf9dkTA31lJN2h3sSD83PigeH5DNjUvn
JiSTg+LHHaLuZjw+IFmY8AA2R/u5gYd0qJsbfczOTXhNj7nPCAnR6+WMz19m
A4DBF5NeL6d9fp71eT4tfdVGSp5PiRem+XnwpZP8zISwEy6Y3ulBfmpY1N/O
GdSoqgQry6g8H1v0rMvB6tRYJUfKMtTk4vr7fRxWXlnGqMow1FpwiwFAsBAa
OVaXQz2GaxVIr0EWA5z3+vK7d4Gg34cf+F3o/rfD9guICeh9vHnHrk07dm/4
6ONNO3Zt3R2+BezorqBNu0I3A4AhUZtCw+F1C1wctGdLyN5NodEbQqI3huzd
GLJvc9j+Df/piI88GBi2b21wdGDInsDQaDgODN+3VmAwam1oxLqQyMDQqHWh
kWtD964N3QNIrgmGPAjiGPUKRrj4oIefv4dfgKd/gJd/APyFP6/2nvB/LcD/
dT9/gT5fr9d8oHgu8fZcucTzq69kR0/yp07yl2MBQHrpAgsMxl4RXbkGJPJX
b/DXbohuxIlv35MkJnvcS3SPvydOzpClQyrMF+UXi8srpQqltKKSrahm1Tqx
RitSq1hVFVFXs9UqotSItQZereZunRPt2Cpa4kl8JGIfb7GPD/Fx59atEn3+
jeTrI9w3P+Ijx9CJY8zJo26njqFTPzJnj+HzP6L0BFyWgyoLaW0lseg5nZoB
Z1JTjrTVxKwj9TYWTtaqqUHLWnRwATDIQo3qMFNgsMHK2fSkvo4DHWxzSRxG
1m6kTiNpqWPb7KTDjp80c0IkdAkYCkNJTdippAW3cdott7jzKPZ7JvYrt/jT
5NpRfOl7txsnUNwZJukSij+Nbp9krn7HHPkMHf2aOfcjunYBZ9wn+amoKJ1J
vYnvnkYp15n0OGCQSb8qeFF5NlLIUVoi1pSTJgsxVKHKLKyTUwBBmYOU+cSp
I49bhEXdwV0LDFpIm5E2qGm9ilanM4oMpMllDCXEUU1cCmwpx8DFyCPuUb3Q
Q2rXY30lzYtnqnKwRUMfC5vmYOUDkn8e14IOCr2WGKTQqCTqYqzIBMVEcKAH
Q1gDzNKRJ9LxQSlI3sy4bHbCc7xf1NtOO1voxID0+aRsWsCQBykcfChsEDk9
5jE55Dk94jE/JZD404wfAPh8wuPFlNdPz/xBIufHxc9G2Ocz0jmImZOi6XHR
5Jh4ckQqTEEaAtkFZ4IVpbiqBClKSGkW1oPftrG6GqIoQ9VluMEhfvzE02nn
qksxaGV1CdxoWqMQkKwuISpQQ+CxkjHWELsFK8pkMZ/+bnNw1O8jP30v6n9/
H/bZ9pDo7cHhoHrbQ/dvCQrbsjtom4Bb5ObgkE3B4RtD9mwOjYISGBQeuDt0
Q3BoYFDwut3BgcFhgcGRG0P3boo4sCEiZkN4DEje6uDItUAWsBa2B06uD9+3
DqgMjV4HGIZEvlLDMAFG0McQOAMkRq8Fm/qq/2I9MLh0yX+K12tLfJcs8lu6
2H/J4kWLFy1ZHLB0ScBrAUJTzOv/ZdD9rdc8v/rS/fARevwof+4Me+E8PXWK
Xrgouhgrjr0Chb9yU3Ttluj6bfGdBPfbd0ATxYmpXsmZ4rQsUXa+pLBUUlxM
y8rYCoVIWQsw8goFq6rmqytpVRVVqsS1taLMJC7qfXapp8hbxgV4iAM8WT9P
AjoIDPp78OFRnt8cpd8exj8eZY4fZU4fRyeOuJ09jk/9gK6cQrlpuCgLV+RT
nZroIJ5XIhXUhwqkUyG7mdrr+BolV6thjXrerKPAoNMstgFoVuqyiewmgcEG
K/hVkdPCw7HTJHQdCtsrW1B3A9/TwD100S47flTPttWRZhOrzqHJsUziTbcr
P6ILX7sBhoDehW+Ziz+43TyDbpxi7pyHMwzI4tkvmCNfoSPfojM/oMvnUPoD
kpOKclPxvSvozimUfB2lxuHkq25pN0AZGXkOU1WGUhMx1CRNVqKvZCpzsL6K
mKtJdS5TlU+sWtzdzHU2c8Cgs4ZtswpBrx541OCqdAbCoyqH0RZiq5wYi5iK
NPSwHaydYF+dkJuEfU9ISQoqSkHqStLeRMFStuj57NMITGlNNlLnktoCZIVf
YBVWFuKqLDdVHq4pAyqpTct2NNCxAdlov2R0gH826Tk7Khl+LOpuo73tZHpU
Nj/pOTMiHekT1n0deCgsOz857Ds64D45LIIvPZ/yejHj82Lad2Hc4/kEaKLf
iylvCJhgQZ8LCZGbmZBMjYmmxqWTw5KJQXc47u+UKvKwvIhWFnHlhSg/g9Gp
aZ1ZpFECmLSy2M3l5Hsf+1kMXGURUw7VbwHSqjD8XJVFuLIYKcuJGjSx0s1g
gNxBcrK8dsXseC/qmw/3H/6fvd+9G3Xw95Exv4s8+HbkJ9sioreFh28NC9sW
vmdzWMT60LD1oVFbI/ZsDt+zPgSgC14fHLx21+63PtqxatfONcFBG8KiN0cC
PvvXgeQBUMF7oKwOiVgXvicQTobug/OghusioOxdFw5sAoMRwOnqoMg1kBAB
QMGaHhDabcI/cV/xhsfyZV7L3/B+c5nv8tf8l78WsOy1xa8vXfzaoiVLF72+
xH/ZIt/X/HyAwaVeHqCDX/xZ+v0hdOg7cvI4d/QIOX6cO3OOP3eBP3+Jv3RV
fOm66MoN/sYd6dUbYigJKe6JGZLULGl6tjgzV5qbLyoqFZVVSisUkooKVl5G
q+C1gsrlRK0RleSzhz7n1r0u9ZFKF/uIFnuLgEE/D9ZfxvlJRd6AoRj/8Xce
3x3hvjuCjoD/PIZOHmNOnUAnf2SOfuV2J5bmpDMFGVheSLVKopJjqCrVcqa2
GkNYcNVxZiOrVAhzpgx61qijdQbOYeKtBtZh4Zx1YrA6diNptApTp+Eht+uJ
Q48arVxTHWm10p5GvstOuhy00467XBQSGTz8GdfR/Vh06xw+/zVQ5hZ7iLl0
iDnzpdvFQ8z1U8LI1WunmCtHmAvfMEc/xcd+YA99zZz+jrlynkl7QDIfoJxk
Eh+LANLEa+jBHZx4xS31DpOZgMpykbyUpCYirYI01VFdFZHnIoOSmpSkMoeR
5yGzFnc2gPpwRjWCfNcCsdRInMCjGsnTmdJkpASU8hgjZKVclBXHuOzc6ICw
+GqrjdFXE6MGyfNo9j2mooh3WNjBHtlAB61JR4UXiSYLawrhu6jQsKyh6nJG
VYirs4VXbQUSIrZRmKEJUjj8hB8flACGU8OSoR72URt58oifm/AG1iaGJE97
6UA3198F9lU6Puw5/EQ6OSJ7NiGbBwynA15M+c6Ous+OeD6f9H8+6Ts1BPmR
n5+UTI5ws1PimQl+ChzpiBhgnB0V6ytodhIpLyIVJbggm2YlI42Cmo28WoEr
i4i8CLscks5ud30tqcjDpRlgU6lWxSor4NfIyItALgnUw2olMpmg1mXi41//
IPrABzGHP9j/zbvRB363Z//b0Z9si9q3fU/0tkigL2RLROTGMIhvwetCw7ZG
7tkeuXdzWGhgcFBgcOiaj3ev2rlj5a4P1wTvXh8evSlq/4aomMCI/eteAbgm
5JXPFMqeNWF7Aa51YfvXRcVsiAK5jNoQCRhGvhUcsTIofHUQiOD+1UFCmwxI
4YbIA+6rV3ivWumzaoX36hVeq5f7rl4RsHJFwFtvLlnxxtI3oCx9/TX/1wRB
9AIvutzX68Be929/oN99gw9/R3/4lhw7wZ88y508x545x16IFV28Ir5ynY+9
LD4fy99MlN19IL6XKksBHczgU7P4vGJxcbkYMCwqpiVQRZfR8jJaWkaLi9nz
x8TvrhcvEUsCPDyW+Lgv9pYFeIn8PEQ+7ryfu9hPKvaVcV4cu2md9JtD/A9H
mKNH0dEjzPHj6PhhfPQ75tj3TMINnJ2CoaqsKiXVclpRQipLiaqS1FRhk461
W1mtmlVXgxGltVpi0hOrkTNr2TqTMALHZmbBrDogGNpZi4E1qolNS5x6DAg4
TQS8aKeTttsJlE67wEWjkajzye0zzJ1LzMXD6OzX6PSXbhe+dzv7DXMSDo4I
nZXnDgkHIIvHD6BDYER/QIe/ZU58y1w+j9MeoIz7KOsBc/MivnycuXeVSbrJ
gCYmx6H0e6g4D5WV4JREpFfiJitfqyDyAgQyBFAAjBB4QcvanFxHCzWosbUW
NZhxk4k4BE2klRlMYZLgXatzGE0pVuXjlGuMRoEHekSgd50t4loFra1mwNpl
J6GibMhQuLdDMtTLtdeR0pu4Il4YSgoYqvOQUUHhA2jKkLIAK/OQqghpy1Fd
LWRq/PghO/JUNDTAT456zIAjHRQ9eUS72+lAr3h2yn123H3sKf+0V9ihoK+b
HX0qGX4qHXosmMxXWgle1Ht+3GtmxPPZiNfcuM/cmI8wgHNCPDVGp0ZEc9MS
CIYTw5LpMcnMuKSjgYu/5JaaQIvzUVkhAQbTE1FVOaethQqclBXiihLU1CRr
bZdplKg4hwGTryrn4GcEAIuzmLICwbUqy7FWg0wGpFGxXxza/Pvoz/+45+C2
6Ijt0dFbo6M3R0VtiYpaHxG6PjRkA5SQ4LWhuwODd20JD9kSFbYxFPxn0Nrd
IWt2hwTuDnkrePea0JB1YVHr9+zbGB2zPmLvqt1ha3ZHrQmJXBUU8lZQyOrg
iFVBEWA114UfWB91cEPE/vWggCEhq3aHLN8ZsvLD0BU7w9/cEfbGB0HLPwIe
QS5j/h+7DNtY
"], {{0, 200}, {300, 0}}, {0, 255},
ColorFunction->RGBColor],
BoxForm`ImageTag["Byte", ColorSpace -> "RGB", Interleaving -> True],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSize->Automatic,
ImageSizeRaw->{300, 200},
PlotRange->{{0, 300}, {0, 200}}]\)Definissez un motif.
In[9]:=
motif = FilledCurve@
BSplineCurve[4 {{0, -.75}, {0, .75}, {1, 0}, {1, 0}},
SplineClosed -> True];Visualisez-le.
In[10]:=
Graphics[motif]Out[10]=

Construisez une tête de tournesol à partir de celui-ci.
In[11]:=

Graphics[{EdgeForm[
GrayLevel[1]],
Table[Rotate[Translate[motif, {Sqrt[i], 0}],
i GoldenAngle, {0, 0}], {i, 100, 0, -1}]}]Out[11]=