Utilisez la décomposition de Smith pour analyser un réseau

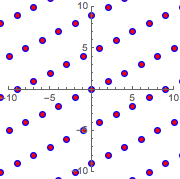
Considérez le réseau 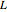généré par des multiples entiers des vecteurs 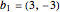et .

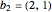In[1]:=

b1 = {3, -3}; b2 = {2, 1};

In[2]:=

ptsb = Flatten[Table[j b1 + k b2, {j, -12, 12}, {k, -12, 12}], 1];

In[3]:=

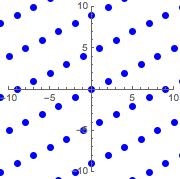
graphicsb = Graphics[{Blue, PointSize[Large], Point@ptsb}, PlotRange -> 10, Axes -> True]

Out[3]=

Soit 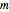la matrice dont les rangées son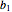t et .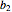

In[4]:=

m = {b1, b2};

Les trois matrices de Smith donnent la décomposition qui satisfont l'identité .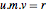

In[5]:=

{u, r, v} = SmithDecomposition[m];

In[6]:=

u.m.v == r

Out[6]=

Les matrices 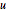et 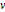ont des entrées de nombre entier et un facteur déterminant.

In[7]:=

{u // MatrixForm, v // MatrixForm, Det[u], Det[v]}

Out[7]=

La matrice 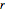est entière et diagonale. De ses entrées, on peut voir que la structure du groupe 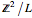est 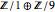ou simplement 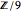, comme 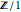est le groupe trivial.

In[8]:=

r // MatrixForm

Out[8]//MatrixForm=

Le fait de multiplier l'identité 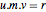à droite par 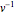donne 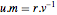. Le fait que 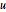est entier et déterminant 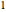, 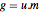génère le même réseau que 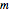mais est plus simple.

In[9]:=

g = r.Inverse[v]; g // MatrixForm

Out[9]//MatrixForm=

Visualisez le réseau engendré par les rangées de .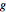

In[10]:=

ptsg = Flatten[ Table[j First[g] + k Last[g], {j, -12, 12}, {k, -12, 12}], 1];

In[11]:=

graphicsg = Graphics[{Red, PointSize[Medium], Point@ptsg}, PlotRange -> 10, Axes -> True]

Out[11]=

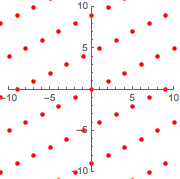
Avec la superposition du nouveau réseau sur l'original, on peut voir qu'ils sont identiques.

In[12]:=

Show[{graphicsb, graphicsg}]

Out[12]=