Wolfram Language™

Résolvez des problèmes combinatoires à l'aide de Permanent

Un permanent est semblable à un déterminant, sauf que tous les termes ont un signe positif.

In[1]:=

Permanent[\!\(\* TagBox[ RowBox[{"(", "", GridBox[{ { SubscriptBox["a", RowBox[{"1", ",", "1"}]], SubscriptBox["a", RowBox[{"1", ",", "2"}]]}, { SubscriptBox["a", RowBox[{"2", ",", "1"}]], SubscriptBox["a", RowBox[{"2", ",", "2"}]]} }, GridBoxAlignment->{ "Columns" -> {{Left}}, "ColumnsIndexed" -> {}, "Rows" -> {{Baseline}}, "RowsIndexed" -> {}, "Items" -> {}, "ItemsIndexed" -> {}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}, "RowsIndexed" -> {}, "Items" -> {}, "ItemsIndexed" -> {}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\)]

Out[1]=

In[2]:=

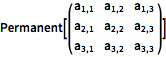
Permanent[\!\(\* TagBox[ RowBox[{"(", "", GridBox[{ { SubscriptBox["a", RowBox[{"1", ",", "1"}]], SubscriptBox["a", RowBox[{"1", ",", "2"}]], SubscriptBox["a", RowBox[{"1", ",", "3"}]]}, { SubscriptBox["a", RowBox[{"2", ",", "1"}]], SubscriptBox["a", RowBox[{"2", ",", "2"}]], SubscriptBox["a", RowBox[{"2", ",", "3"}]]}, { SubscriptBox["a", RowBox[{"3", ",", "1"}]], SubscriptBox["a", RowBox[{"3", ",", "2"}]], SubscriptBox["a", RowBox[{"3", ",", "3"}]]} }, GridBoxAlignment->{ "Columns" -> {{Left}}, "ColumnsIndexed" -> {}, "Rows" -> {{Baseline}}, "RowsIndexed" -> {}, "Items" -> {}, "ItemsIndexed" -> {}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}, "RowsIndexed" -> {}, "Items" -> {}, "ItemsIndexed" -> {}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\)]

Out[2]=

Ainsi, l'application de Permanent à une matrice dont les entrées sont égales à 1 est un moyen amusant mais inefficace de calculer la fonction factorielle.

In[3]:=

Table[Permanent[ConstantArray[1, {n, n}]], {n, 10}]

Out[3]=

Le permanent peut être utilisé pour résoudre le problème combinatoire le plus intéressant suivant : étant donné ensembles, chacun contenant un sous-ensemble de 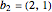, combien de façons y a-t-il de choisir un élément distinct de chaque sous-ensemble ? Tout d'abord, construisez la matrice 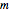où la position 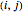contient un 1 quand le sous-ensemble contient 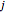, et zéro dans le cas contraire.

In[4]:=

sets = {{3, 5, 6, 7}, {3, 7}, {1, 2, 4, 5, 7}, {3}, {1, 3, 6}, {1, 5, 7}, {1, 2, 3, 6}}

Out[4]=

In[5]:=

m = Table[If[MemberQ[sets[[i]], j], 1, 0] , {i, 7}, {j, 7}]; m // MatrixForm

Out[5]//MatrixForm=

Le permanent de 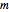est la solution au problème.

In[6]:=

Permanent[m]

Out[6]=

Confirmez la réponse en construisant explicitement tous les tuples.

In[7]:=

Select[Tuples[sets], DuplicateFreeQ]

Out[7]=