Use a decomposição de Smith para analisar um reticulado
Considere o reticulado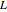 
gerados pelos números inteiros múltiplos dos vetores 
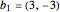e 
.
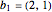In[1]:=
b1 = {3, -3};
b2 = {2, 1};In[2]:=
ptsb = Flatten[Table[j b1 + k b2, {j, -12, 12}, {k, -12, 12}], 1];In[3]:=
graphicsb =
Graphics[{Blue, PointSize[Large], Point@ptsb}, PlotRange -> 10,
Axes -> True]Out[3]=
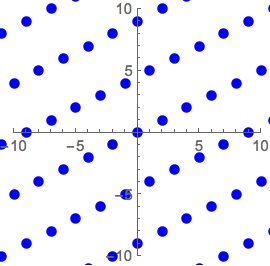
Permita que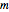 
seja a matriz cujas linhas são 
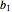e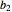 
.
In[4]:=
m = {b1, b2};A decomposição Smith dá três matrizes que satisfazem a identidade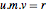 
.
In[5]:=
{u, r, v} = SmithDecomposition[m];In[6]:=
u.m.v == rOut[6]=
As matrizes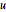 
e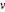 
possuem entradas de números inteiros e um fator determinante.
In[7]:=
{u // MatrixForm, v // MatrixForm, Det[u], Det[v]}Out[7]=
A matriz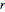 
é um número inteiro e diagonal. De suas entradas, pode ser visto que a estrutura do grupo
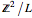is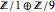 
ou simplesmente 
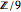, as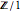 
é um grupo trivial.
In[8]:=
r // MatrixFormOut[8]//MatrixForm=
Multiplicando a identidade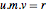 
a direita por 
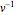resulta 
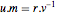. Como 
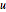é um número inteiro e fator determinante 
, 
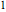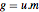gera o mesmo reticulado como 
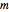porém mais simples.
In[9]:=
g = r.Inverse[v];
g // MatrixFormOut[9]//MatrixForm=
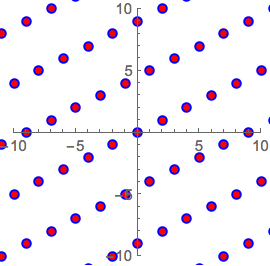
Visualize o reticulado gerado pelas linhas de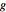 
.
In[10]:=
ptsg = Flatten[
Table[j First[g] + k Last[g], {j, -12, 12}, {k, -12, 12}], 1];In[11]:=
graphicsg =
Graphics[{Red, PointSize[Medium], Point@ptsg}, PlotRange -> 10,
Axes -> True]Out[11]=
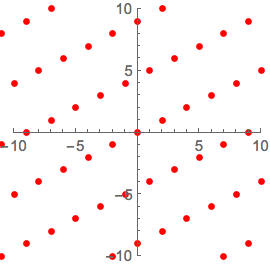
Sobrepondo o novo reticulado sobre o original, podemos ver que eles são os mesmos.
In[12]:=
Show[{graphicsb, graphicsg}]Out[12]=
