Tweetez-un-programme
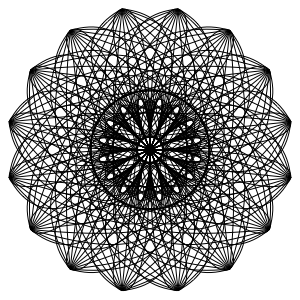
AnglePath et CirclePoints peuvent produire des résultats esthétiques dans des morceaux de code compact, ce qui est idéal pour Tweetez-un-programme Wolfram. Voici des exemples de tweets par les utilisateurs de Wolfram Language.
In[1]:=
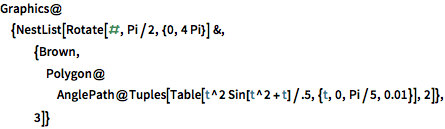
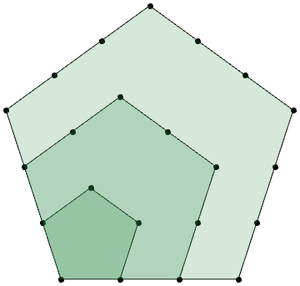
Graphics@{NestList[
Rotate[#, Pi/2, {0, 4 Pi}] &, {Brown,
Polygon@AnglePath@
Tuples[Table[t^2 Sin[t^2 + t]/.5, {t, 0, Pi/5, 0.01}], 2]}, 3]}Out[1]=

In[2]:=

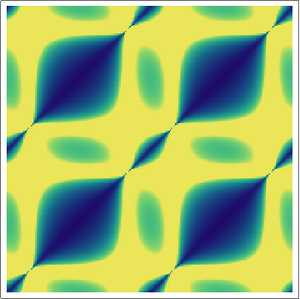
Graphics[{Polygon[
AnglePath[Tuples[Table[Sin@t/8, {t, 0, 5 E/8, .03}], 2]],
VertexColors -> Table[Hue[i/3250], {i, 3250}]]}]Out[2]=

In[3]:=
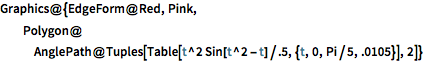
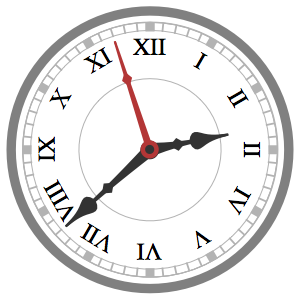
Graphics@{EdgeForm@Red, Pink,
Polygon@AnglePath@
Tuples[Table[t^2 Sin[t^2 - t]/.5, {t, 0, Pi/5, .0105}], 2]}Out[3]=

In[4]:=

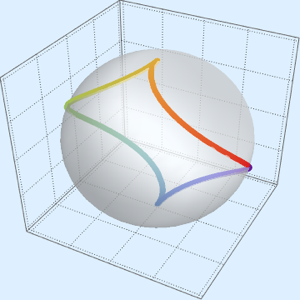
k = Tuples[Range[-2, 2, .15], {2}];
Graphics@{BSplineCurve@Sin@CirclePoints[#, .14, 25] & /@ k, Red,
Point@Sin@CirclePoints[#, .15, 2] & /@ k}Out[4]=