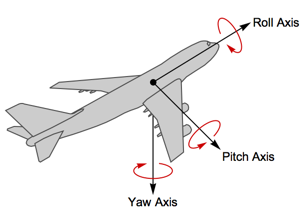
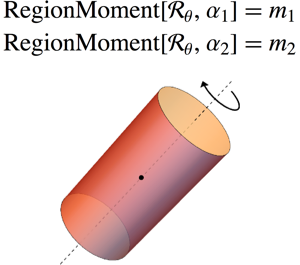
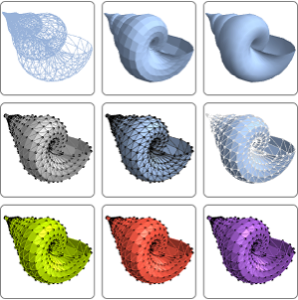
Eigensysteme über Regionen
Berechnen Sie die akustischen Eigenwerte und Eigenfunktionen für eine Approximation eines Querschnitts durch einen Mini.
Importieren Sie ein Bild des Querschnitts.
In[1]:=

img = Import[
"http://upload.wikimedia.org/wikipedia/commons/d/d3/Mini_cross_\
section.jpg"]Out[1]=

Verwenden Sie das Masken-Tool, um eine Konturengraphik zu erstellen.
In[2]:=
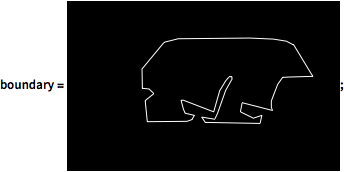
boundary = \!\(\*
GraphicsBox[
{GrayLevel[1.],
{AbsoluteThickness[1], LineBox[CompressedData["
1:eJxdkmtI0wEUxZdKWCaazxQlHyQLRckXQmQH+2sWCs5HivlhSYaKjxbF8rU0
0U2n8ndzsyznllvbSkrRAidGPjPMkmI0bRk+FlqZm8+cJRXkhD4cLj8OF+65
HM/0/PgMMwqF4vtHf+eGPMHP+YQAI1FXm8O8ROippM+RZbdQwGJaJa+IkFuR
PX+OK4WZnvh+1L0FfBubH8nxcnQN2TblTonwOmtLGapWwImhMKzSRZj+1TH+
sl0JSWm43WJhM2SF7OFM3UP4ExzZYIgQbg0B28v2SkjfqvoNVkLwGVGqwHQF
Prkk0iw3BDh2kSkefyMH60HstdHEBkTqJlvv2MuR8ozRulRCmtisjJFoZVWH
HOPq2GagHNTysPMSXg1SDZ19A49bccPrcg7dkUSed5BPcVErKL1m40lfuVCU
HNakbksR10d+LDNyMOujp8ZsyiCO/bly6Ew1NlLyay2GZIArm+/DrsSySxRl
ZFQEbd7S8RYLNiJmInhKYzP0jpsVRmYV0kati4JKxejKoYbsK+Eg/5ECE+/E
mFx/RewnuDi9NaRJGpQgO6No8ayBh6DCdHV16T1YsuJdC+oEJs7iegZ/8BDC
o/GFjc5vl3f2/WfiZheOCNCr0TYI7CS43+ZQfEHLQ/DTlTg1XWzKR6RmVIX3
3MZMwMnKfjmJ2Rhhvpa6yzv+8HuxuattLdzWLz0f824y3eumUhPlp+6a/qFq
2+vr2XEH1K3U+NAEDtbqMzfSappwfSB5zvkmG9bmBxdotHroadV7IlPY//KT
cGdqHCZ4JJTd7QmyKR5Yn6f0jiE86ER2HtPd9WBFO3XqCT6i5688qfUjYama
FQzk8VEecICQOpNIyllb/vKtEf/38zd0gE9/
"]]}},
Background->GrayLevel[0.],
ContentSelectable->True,
ImagePadding->{{0., 0.}, {0., 0.}},
ImageSize->{273.3999999999956, 170.4},
PlotRange->{{0, 3910.}, {0, 2535.}},
PlotRangePadding->Automatic]\);Diskretisieren Sie die Graphik.
In[3]:=
bdr = BoundaryDiscretizeGraphics[boundary]Out[3]=

Berechnen Sie sechs Eigenwerte und Eigenfunktionen des Querschnitts.
In[4]:=
{vals, funs} =
NDEigensystem[{-Laplacian[u[x, y], {x, y}]},
u[x, y], {x, y} \[Element] bdr, 6];Untersuchen Sie die Eigenwerte.
In[5]:=
valsOut[5]=
Visualisieren Sie die zweite Eigenfunktion im Querschnitt des Autos.
Den kompletten Wolfram Language-Input zeigen
Out[6]=