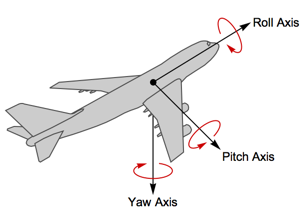
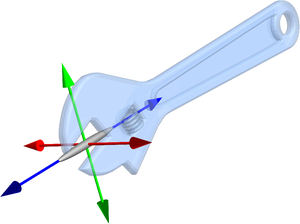
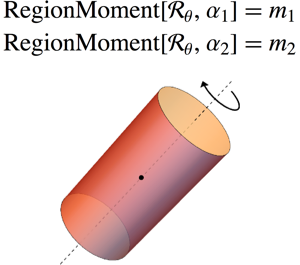
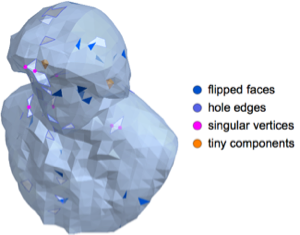
Momente von Regionen

Dan in Version 11 die Darstellung von Momenten als Polynom unterstützt wird, kann man leistungstarke und flexible Tools nutzen, um zu vergleichen, klassifizieren und Eigenschaften über Regionen zu berechnen.

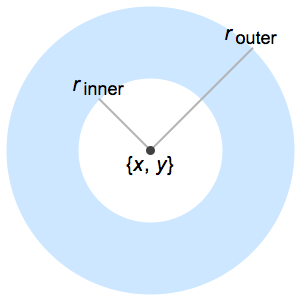
Berechnen Sie symbolisch Regionsmomente.

In[1]:=

RegionMoment[Disk[], {0, 0}]

Out[1]=

In[2]:=

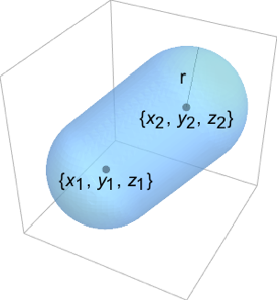
RegionMoment[CapsuleShape[], {2, 0, 0}]

Out[2]=

In[3]:=

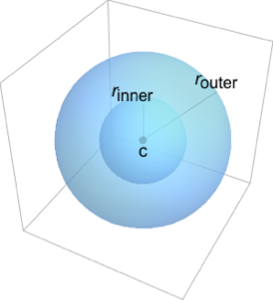
RegionMoment[Cone[{{0, 0, 0}, {0, 0, 1}}, r], {2, 0, 0}]

Out[3]=

Gegeben Sei eine Region mit unbekannten Parameter, wobei wir wissen, dass alle Momente der Ordnung Null und erster Ordnung bei 1 liegen. Berechnen Sie die numerischen Werte der Parameter.

Definieren Sie die Region und die Annahmen über ihre Parameter.

In[4]:=

$Assumptions = r > 0 && x > 0 && y > 0 && z > 0;

In[5]:=

cyl = Cylinder[{{0, 0, 0}, {x, y, z}}, r];

Berechnen Sie die Momente der Ordnung Null sowie erster Ordnung.

In[6]:=

cfs = {{0, 0, 0}, {1, 0, 0}, {0, 1, 0}, {0, 0, 1}};

In[7]:=

{m0, m100, m010, m001} = Table[RegionMoment[cyl, c], {c, cfs}]

Out[7]=

Lösen Sie nach Parametern, wobei alle Momente der Ordnung Null oder erster Ordnung 1 sind.

In[8]:=

sol = Solve[{m0 == 1, m100 == 1, m010 == 1, m001 == 1, $Assumptions}]

Out[8]=

Ermitteln Sie die Region.

In[9]:=

cyl /. sol

Out[9]=

Approximieren Sie deren Radius.

In[10]:=

N[cyl /. sol]

Out[10]=