‹›Probabilidade e estatística aprofundadasEstimativa de distribuição mais rápida
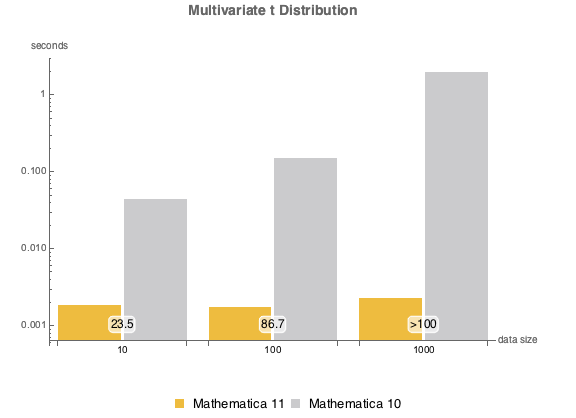
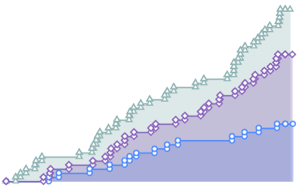
A versão 11 inclui diversas melhorias para estimativa de distribuição, especialmente no desempenho. Os gráficos seguintes mostram os tempos de estimativa de várias distribuições com diferentes tamanhos de amostra. Os experimentos foram realizados em um sistema Windows 10 com um processador Intel Xeon E3-1245 v2 3,40 GHz. O número na parte inferior mostra o quanto que a versão 11 é mais rápida versão 10.
Distribuição 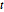 de Student.
de Student.
mostre o input completo da Wolfram Language
dist = StudentTDistribution[loc, sc, df];
ndist = StudentTDistribution[-1, 1, 2];
Table[
sample = BlockRandom[SeedRandom["MarketingExample"];
RandomVariate[ndist, n]];
Mean[Table[
First[AbsoluteTiming[EstimatedDistribution[sample, dist];]], {5}]]
, {n, {10, 100, 1000}}]
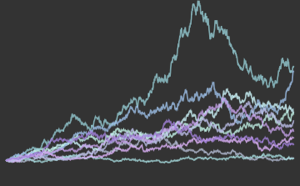
Distribuição de Weibull.
mostre o input completo da Wolfram Language
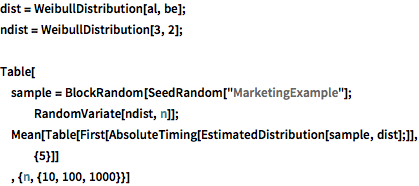
dist = WeibullDistribution[al, be];
ndist = WeibullDistribution[3, 2];
Table[
sample = BlockRandom[SeedRandom["MarketingExample"];
RandomVariate[ndist, n]];
Mean[Table[
First[AbsoluteTiming[EstimatedDistribution[sample, dist];]], {5}]]
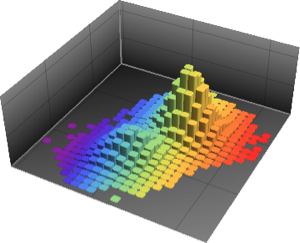
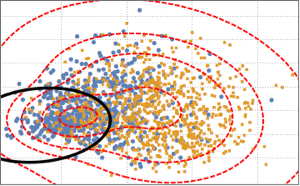
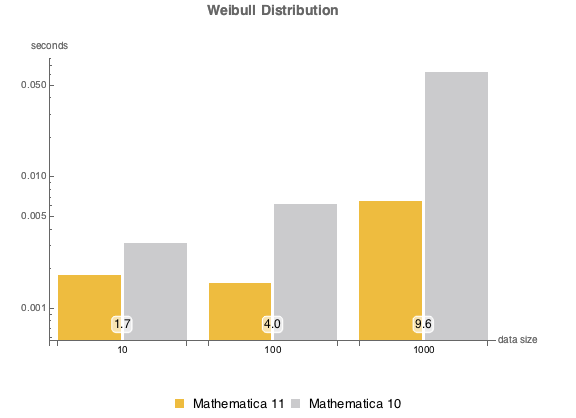
, {n, {10, 100, 1000}}]Mistura de distribuições binormais.
mostre o input completo da Wolfram Language
dist = MixtureDistribution[{w1,
w2}, {BinormalDistribution[{m11, m12}, {s11, s12}, \[Rho]1],
BinormalDistribution[{m21, m22}, {s21, s22}, \[Rho]2]}];
ndist = MixtureDistribution[{0.3,
0.7}, {BinormalDistribution[{0, 1}, {0.5, 0.25}, 0.7],
BinormalDistribution[{-0.5, 0}, {0.5, 0.25}, 0.1]}];
Table[
sample = BlockRandom[SeedRandom["MarketingExample"];
RandomVariate[ndist, n]];
Mean[Table[
First[AbsoluteTiming[
TimeConstrained[EstimatedDistribution[sample, dist];,
100]]], {5}]]
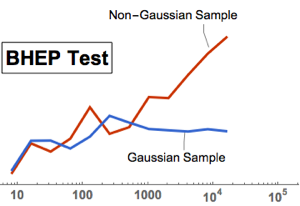
, {n, {10, 100, 1000}}]Distribuição 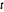 multivariada.
multivariada.
mostre o input completo da Wolfram Language
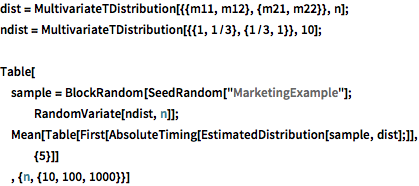
dist = MultivariateTDistribution[{{m11, m12}, {m21, m22}}, n];
ndist = MultivariateTDistribution[{{1, 1/3}, {1/3, 1}}, 10];
Table[
sample = BlockRandom[SeedRandom["MarketingExample"];
RandomVariate[ndist, n]];
Mean[Table[
First[AbsoluteTiming[EstimatedDistribution[sample, dist];]], {5}]]
, {n, {10, 100, 1000}}]
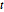 de Student.
de Student.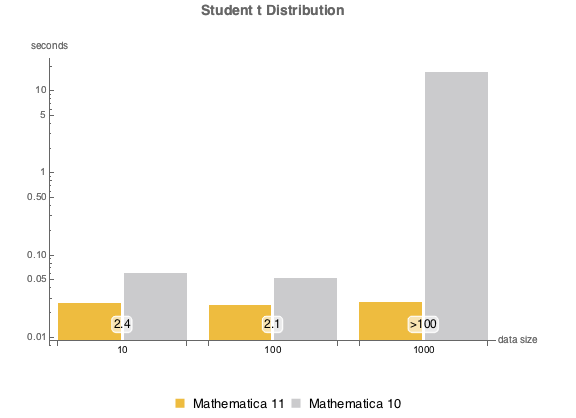
 multivariada.
multivariada.