Retornos logarítmicos de preços de ações: Novos Recursos do Wolfram Language 11

Retornos logarítmicos de preços de ações

Os preços das ações modelados com o movimento geométrico browniano (no modelo clássico de Black-Scholes) são considerados normalmente distribuídos em seus retornos logarítmicos. Aqui, essa suposição é examinada com os preços das ações de cinco empresas: Google, Microsoft, Facebook, Apple e Intel.

Extraia os preços das ações em 2015 com FinancialData.

In[1]:=

symbols = {"GOOGL", "MSFT", "FB", "AAPL", "INTC"};
prices = Table[
   FinancialData[stock, {{2015, 1, 1}, {2015, 12, 31}}], {stock, 
    symbols}];

Calcule os retornos logarítmicos.

In[2]:=

logreturn = Minus[Differences[Log[prices[[All, All, 2]]], {0, 1}]];

Filtre os retornos logarítmicos com ARCHProcess de ordem 1.

In[3]:=

fdata = Table[
   {\[Kappa]1, \[Alpha]1} = {\[Kappa], \[Alpha]} /. 
     FindProcessParameters[lr, ARCHProcess[\[Kappa], {\[Alpha]}]];
   MovingMap[Last[#]/Sqrt[\[Kappa]1 + \[Alpha]1 First[#]^2] &, lr, 2]
   , {lr, logreturn}];
fdata = Transpose[fdata];

Compare os dados filtrados de cada ação com a distribuição normal com QuantilePlot. Para as cinco empresas o comportamento assimptótico apresenta uma divergência respeito à normal.

mostre o input completo da Wolfram Language

In[4]:=

MapThread[
 QuantilePlot[#1, PlotLabel -> #2, 
   PlotTheme -> "Detailed"] &, {Transpose[fdata], symbols}]

In[5]:=

{\!\(\*
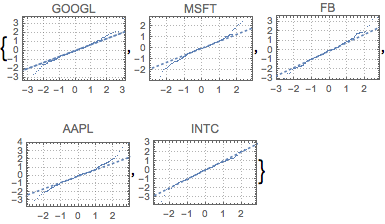
GraphicsBox[{{}, {{
{RGBColor[0.368417, 0.506779, 0.709798], PointSize[
        0.007333333333333334], AbsoluteThickness[1.6], Dashing[Small],
         LineBox[{{-9.739549144845185, -3.2234018878885635`}, \
{-4.914315914292211, -3.2234018878885635`}}]}, 
{RGBColor[0.368417, 0.506779, 0.709798], PointSize[
        0.007333333333333334], AbsoluteThickness[1.6], Dashing[Small],
         LineBox[{{5.389488258896621, 3.6124508317404134`}, {
         9.174325346727695, 3.6124508317404134`}}]}, {}, 
{RGBColor[0.368417, 0.506779, 0.709798], PointSize[
        0.007333333333333334], AbsoluteThickness[1.6], 
        Dashing[{0, Small}], 
        LineBox[{{-4.914315914292211, -3.2234018878885635`}, {
         5.389488258896621, 3.6124508317404134`}}]}}, {{}, 
{RGBColor[0.368417, 0.506779, 0.709798], PointSize[
        0.007333333333333334], AbsoluteThickness[1.6], 
        PointBox[CompressedData["
1:eJwVlGk4FIr7hscuEqnkWE6WKBGFX1HpHZUlHMmpSClLhRJOlhTFkaVCFCFR
CUW2I7KWd4Tsa4Ns0yyWsTODxv7v/+G5nuv+dl/Ph0fewd3yKjeBQFj8nf/v
AyXvYwc4G0g8tSQDEkGZJJR3ylL5oABp70n3cpWnQiSZioK0lUw+EuN/XrQi
HT5SyQt1u5xIXlLGKhv0B3hITJldjpY5PCTzq4Nf6tK4SQoSQ7ZBLG7Szsgp
b8zkIolJOWRFnuYmFWbZi7Ak1lFMZOrEkyouUv4RsuKNhTUsaXEbkzjBRRof
3zq07fQK8prtPqLYRiCxf019Muzi4C4JmnbEVQJpA/eU5J58Doq/br5Uxk0g
OYxNah5+z8HPlp27ps3WkcbotpyK4mC0vbF02us17B5f2NhR+guFKqz5t6ys
Yn+9iVDU1wWsX7rXymu/ipcpmw7+7/0CSldJbr3bvIIGVW9598/P44U7hv6v
iCuoKu2qd3HbPN6zrfTD0mXMesOesFtjY+zQhn8MdJbRzqRjzmaJjZKaAv/k
li8hg3ZZ8UcQG0+R3IweH1/Chlv2kmeE2Hj8TPL5262LSJHJ9ZugsrBDboem
3OVFFNRS8OiisNBTJytcl8VBT3aluWYyC/fcy/wS+JCDes0cxb3uLDxwiehV
Js/B4P/tkbqhxkL3j4Gp+V9+4QFJ13JfURamXzfLPHDxF4ZMp14ctZrFvqoH
sX+uLmBvpE6RjcUs0tLVHx97s4CisUtP7u+dxQnj+WMBBgtokRLuenvrLFoK
eiYVTszjS+XnFuemZ1AV+w7VPJ/HhGiHqeiy3/xUQSeOOI9bFrZ8l3edwe6A
S5RNk3PI31kQubFnGqkV8TckX87hHZP4kPCqaSQ2BAwkm8wh386los0lU+h/
sq8qfJmNLqf/OMlzewprRl5KtuWwsfTmDy3TM1P4MpIsY2PPRhtF+Rzja5M4
qd6lKyXBRl3Oz7vmOybwnCd1iKuJhUYspu9w0DhqwWg4zwMWXov2Dz52eRxf
pG/2ET/MwvMiN3vfW40jm+FWpjA3ixx/cwUj2ijmX+5TUcmdxUeBbRW8ZCbu
LHtClHaZxddW45pHXzORaW0gOb1zFod0Rdu1nEfwVUTthZe0GTQLTz2QvGEE
ZcTfH97+egbZ05mBDiNDaKMjesXGdgbfvrAVTkgZwrjsh+yLMr93kvMT+eA8
hD8HVYfUS6bxrsE1/5KjDFxakE/g051Gq/bIyh1iDGwLuR6xr3wKPW/ISmkS
6Xj6v4ect0enMFfDh/z8Iw23MFzyLaomETcU7msLp2ES95cd6icnUWSU+ebB
PRpqf1c5sK9tAlWLxYWXb9KQmW3pbGY9gXyeho7ORjTU4I5860sbx3UbKlsK
aFjpBMeyboyjh2djWJ4gDTfndW7qWxhDnaLqx/e4aJhupqe1HjSGZa7eBw2a
qVhUPHBQVGwMl4Y5B1ozqehawrXK/WoUN+s+P1fvR8Wq8vefOtRGkVuZEZph
TMWM4//RfT4zUXun2g6J7VScd3UwZ5ox0U97sHWPMBU3m4OgHGUEs+0enSmP
piAnVdZ+u8cIfvPc4v7Bm4Jh9LCRWu4RtHrTWnN3HwU/m1pdUY0bxleLPx5O
Fw3gnEZY9+E9w9gWV6jeGjaADuOHvdkVQ3gkzb769OUBLE5cfGt2ZgjVVer3
37YcwOR+/nn9sUEccVJRb1UcwBwjjmpL4CAGCNrdFp3sx/FQe82J7YOo3lvj
+Mm2Hw1PZ0rF5zHw/KTstbzGPpTIWZVpMGJgiohASmFFH64oX3seSKWjjYKJ
5opGH5aSZ7mK7tCx31pTsHt3H9qorBOubaEjYVmZ4KrUh4/rXp6KyKHhYj4I
a0IvJmUt1e40pqHvP9fTOWndeGXj+mVVBhVj5SWyLEK68WBG766k+1Q0Yj9b
S7nRhXYbKow9pahIrTws9Hq+EyuOaAnY3PyJumv5Zy4MdiL/cv/l8HcUFJfw
zygK7USMvuDtSR3AUTelkF2unTh3w9REWHoA1Vrs3qzXk1G9ZEHA7Fw/Hrwp
7dCSS8Z/SXYr6s/6sJHmXafw5jtGRDkl5LT0os+mgvv68d/xktXSzUrhXnw8
Op6sdf87th13VL9ysgf7Mi7bH7jRgeiRmhEV9gP7OYdpTkpt6N7xs1bvWzf+
raBDMi5oxZHZgafOfN0Yqx0c/1y/Ba09opSEDLrQMtFdYs6lGdXOZpXKhHTi
cLgjaGc14FbdMy8Ta8g4Z/rnX8qRDWjl1qB2n5+M9TopBSfEG3DRUmWw0ug7
CswIuhZL16ICn4aJ3aMO5J0V1bkYWoP+n0UW/25sR4z7TqmprsYr2wxfxou0
47NNegYyAdWok/poTMmiDZuL9vPcdK3GG6dMbNlKrdiZGiBmUfcV7TMYvtLZ
zSiknqPl4/sVu7gSR0s1mzCqKEzixzoJSxJUw6pLG/Duf4VtWsEkdNW209uv
X4+KlEnztj0kvDMgKbRQV4s8rh9IcrtI+PCU87Lg6W+YmJ9gf+lBBXL2Fey1
66lG8TXLViuPMuyR766fta9ChUQyfYZajM2lVjyFY5U467JVQPBdMfo/i5ZI
9iRhsIrBWYXCQhxb74o0XPyCI2FNjT8+FOJXXe2yO8LlGHJX6sh0XR7uS081
IcmWYMONuaYrtFx8Jralj3/fJ8wYpfvuNcpGHxMPgUPHPmJi3BUcScjCNhOz
toiMXPSOjTPW/pyJb3M0ZPc3ZeBigETn2usMtBXR5Dk0/RajrQxZJbQ3OJHy
YISgmIhmscSNookx2Gbzie3VGIFzKdlS8vvCkTSZrxCteRVvhZhWbPMIQjt2
narowSCQJ4mnxMhegyNJMChPjYXsfOdkQd274Hqrx2/47zfAf91sfWNvCGRv
JJS66r6DP2q8jpfpRcBERqJJk1w2FEP5jsS7SeBz7OfW7Xz54HPAYnhkMAl2
Crd3DywVgHWYj7DfSgpEv582b50tAj4qF2OyOg2kGrxiCGOlkCBb/87R8R0E
c11aDmV8hs0WJTv3jH6EQTe6rC8Fge+ceStfxCdgN/FOeN2sBLLhWOOlveWw
i69g952Jr5AB1oei5b/A3cN+hDOu1SBTsM3JQ78CEo5K9ohN1kArGEao1FZA
7rq0QblbLWjJCXfwV1WCyZFU/suzdfA4adpIur0SPOgK4oLeDdDT8kHYJewr
BG04/fTrYiP8ZRojzyBWA/2O6nBiQDPEuGzuTafVQEefbG4yfytU+jdvI+TX
wbOhNPoNozaw++VNjE9shPMvFneqbmyHq8TM3fEZjbCrYoNFTHs7CLGi3ye1
NoLr7vBDWfEd4FHzl+AGiSZQvk6j3bn0HZaSv6KmbhMoEve48iuTIXzU61zE
o2Yg33PcYz1FhoLvKdaO6c2wzzA70ae4EyRuSxo0+rdAcnDqdZd/u+Cgj3NS
2clW8K0YuqNj1g0MaftW0+U2kA3M7h/f/gMawxauPYV26O56Sgkf/AHmMQki
v/5pBzu/u3zyH3tgSCLz4oUn7fAkLHNrYWAvFKD4clR5O8y0EsTMLfrA/aJL
xjG7Djh6+B/gyPVDao+tU+6tDqj4/ErzM6sfFvfzuFQ/7IBXw+XVqTUD4NfN
caox+A5dDilypS8osCqzwqTLk2E3r3INv/tPeBpZJziSTYYMQ0p1owIVio98
DLesJcNNh9zT5U+owNVB40ldIcOhRQrZapkKac/ra45ROiG7zMv8vTMNzprK
7z7n0AXVV+Lm87posLfIK8W0tQvSH5Qe9jWgg+/PE9YznC64aCPQxv+JDtcr
1FwOYjf4dKy9dVBiAD13p5eBYC/ItVqPPYtjwCEnvi38e/vgWou20mvBQehg
a04r+/SBlWOsXJTfIKjKEBrcOP1QU6O2cn16EBoe1DkPdAyA5/04jcNXhkAx
iVyUTqMAQ3IwSrB3CEQVSFZxLAokVWWe7bcYhqNUMb/yv6kwPBqoSKobhlui
BTsME6hg8cdWkQr9ESjjzpDmuk+D6kXSK2r5CLz9madWk0EDntqfQ5oHmfDY
WFT/aSMNgpMq75AKmJBzxqLSXpQOH0TuhDzfPwp6PBF6oTl0iFkO6qj4bxTi
D8nqJ+TRgebuTD65fwyCWd4zfw/S4WqY96cTBWNQRlCq6nrCgIlD6VcqDoyD
27CewFIaA5gaw2nfyschsocgrpPDgKA6mqzbsQkQC/UbUFUYhNXHXm7fGibg
lLWTunvMIIh3iejTz0yCUZTMtoXOQUikaDt0UichO6A79pz6MAzb3+0pdJuC
BTdbp/agYZB8rsIXvzYF3dIixuZKI2C3ur00Jnoa8k6rxR8IGYETZf/ucxCf
AdntglZaUkyYkwzc8tZ2BpL/+/d8lAYTdngaiUp+mIHwpnSx+xQmdJJDy77/
moGAKd0ujU2jkHhWlTxkOAvszZVKWtWjcMjkuINd/CxsPOZb5r88CurCQp3n
Rmehb2iPIP+HMQiRaVGnHGFB3xF32/W4cQgyCdsv8owF0j8mvwXUjkNWzJ8x
K0wWTImV1q61j4Mh+Y1urT4bwntiNeJdJ0B3f2/g4yQ2ZFqNMAs9J0DrlEb4
tUU2WOiRK1tCJ2B9/tfr+9ZzMOyr1+TwbRJq9dQSF0vnQCNaOe3d1BREjY5f
5/5zHh5JpLy41zENAYJnC+uC50FyXEDfYmIGmqrOBf07NQ92sVb5ClqzoJbd
sNv5wgKUXMtziQ+dhRc/jS2wcQEkPCvKfB/OQrqp1NEO+AWd5lWS6b/51peP
TgvFv+D5ReGommezMOHxySlSmwPEZP7MJlMWdDNdbwkUcUCD/6l9eQ8LCnhZ
t4aPLEJ9j0Uai8YCN/Nqoa/1i8D8uJK422oOFENVvpnZLoHd2U1mbe7zYH+S
d9WGswSdGZb5WwsWgDnB3jzxchmGRBy7TJp+e1EC/zx4cgUC9cLlXy0vgF+9
YeFnrlU49tpH7Z7pL0gvvmlnV7v6+3/DE86rLsIFxRW3J0lr8JTyQaNHYwmq
dj9q9A5eh/4zdGuvd0vwueM48aM+gUjQUth5/9UylPwsfpffSiDeU9xeV6S4
Ci19h86/8+AicgWqnS+fXINYuv8lH1Vu4kMfx+ehN9fh0uXgC+3CPMQGVw0X
RgqB+O3Bhjdyu3mJSauSxsxNXMQMr/S/TD7xEa2shp9uDOAidtxbjeK6LUg8
N6D02mx4I/H/AGfZWgQ=
"]]}, {}, {}}}, {}, {}, {}, {}},
AspectRatio->0.6180339887498948,
Axes->{False, False},
AxesLabel->{None, None},
AxesOrigin->{0, 0},
DisplayFunction->Identity,
Epilog->{{}, 
StyleBox[
LineBox[{{-9.739549144845185, -6.424606331170559}, {9.174325346727695,
         6.123425270436057}}], 
Directive[
RGBColor[0.368417, 0.506779, 0.709798], 
AbsoluteThickness[1.6], 
Dashing[{0, Small}]], StripOnInput -> False]},
Frame->{{True, True}, {True, True}},
FrameLabel->{{None, None}, {None, None}},
FrameStyle->Automatic,
FrameTicks->{{Automatic, Automatic}, {Automatic, Automatic}},
GridLines->{Automatic, Automatic},
GridLinesStyle->Directive[
GrayLevel[0.4, 0.5], 
AbsoluteThickness[1], 
AbsoluteDashing[{1, 2}]],
ImagePadding->All,
Method->{"CoordinatesToolOptions" -> {"DisplayFunction" -> ({
(Identity[#]& )[
Part[#, 1]], 
(Identity[#]& )[
Part[#, 2]]}& ), "CopiedValueFunction" -> ({
(Identity[#]& )[
Part[#, 1]], 
(Identity[#]& )[
Part[#, 2]]}& )}},
PlotLabel->FormBox["\"GOOGL\"", TraditionalForm],
PlotRange->{{-3.246516381615062, 
     3.0581084489092314`}, {-3.2234018878885635`, 
     3.6124508317404134`}},
PlotRangeClipping->True,
PlotRangePadding->{{
Scaled[0.02], 
Scaled[0.02]}, {
Scaled[0.02], 
Scaled[0.02]}},
Ticks->{Automatic, Automatic}]\), \!\(\*
GraphicsBox[{{}, {{
{Hue[0.9060679774997897, 0.6, 0.6], Opacity[0], Dashing[Small], 
        LineBox[{{-8.62501550382003, -2.8523556428167356`}, \
{-4.488098207856721, -2.8523556428167356`}}]}, 
{Hue[0.9060679774997897, 0.6, 0.6], Opacity[0], Dashing[Small], 
        LineBox[{{4.264036280778001, 2.7184936616092057`}, {
         8.32555754281431, 2.7184936616092057`}}]}, {}, 
{Hue[0.9060679774997897, 0.6, 0.6], Opacity[0], 
        LineBox[{{-4.488098207856721, -2.8523556428167356`}, {
         4.264036280778001, 2.7184936616092057`}}]}}, {{}, 
{RGBColor[0.368417, 0.506779, 0.709798], PointSize[
        0.007333333333333334], AbsoluteThickness[1.6], 
        PointBox[CompressedData["
1:eJw9j3k0FArYxi2VRFcitIhkSdy6hTbpnTbK2Et0LQkVJaSMJSWFyJIs3Uhd
WRJlTXbeIfu+7zHD2LcZM2PL8t3vnO98zzm/85zfef569lk6GNzi4uDgWPqP
/+1tgp9+cHHwkE/LejWfTRIlD7ztSw98uYGs5dEXucNchCzobTYfvZ+b7OV9
l9vKeQM5bz2npEmai6y222Qlfw8n+RVVNQFNOMniD7iH62XW8K5Ma9+VLA7y
XbrnFvP+Vfyy9YW2sDQHuXeoLPZL2CquZWe9iL+8jtJDDguBcSuonsdzQvHW
Gp5VSYuWfLKMB9aS9Y0iVrFr11Kt+8ElDE8SU9DsWEG9myeZQ5sXsLWR5nBQ
ZgWLLOZbE9lsrEm3OV7n+RsThWcEuyfZ+GxcUPYpbRnZn6RsO7+zMSAgKGJU
fxk/GM5n/dHDwo9/auYwKpaQl27TY6DDQn2BXV9zzi2hWmhb0j+1TAzWqtz/
uGwRD3CNzPcVMfESKVk8mriIgrs9LYyUmfhK931WaOcCtklvstblY+K9oX63
iTsL+ERPXpM5OIe2oY39Z1bmUdDS+/7d/jkM4HK+eyJ8HicUHe2ozXNYVX3J
99XheRT1j3z13mgOv75TKmLUs9Hi4tqITBsDpUZY+kcd2KgRkrb7izoDW3RV
d4oKsVE8ce8/dYIMHJfK9XPMY2HlJdRN7Kfj4oIQXciShT6+6q0aSEdXdWJr
Dz8LRaRc7uQzZ5F2beJGbB4Ti5NvG5s8nkW/p9sXNW2YmBz7gJcTZrFr9XJj
jhgTlZ3/lnMdnMH15KmIhpo53FC4+UVlwgwekcn5y+XpHKrl8qU8H5vG1N23
3N8rzWECcef6i0fTaEos3io3wcAklZ+9KWrT+KivQIQnloE/u5iZisensDkx
Rf6gCQPNEnhCKeOT6KXrKvFsBwMlt9+MSv8wie9LFeeXmuhosfecNU/eBIq0
Xf/hH0THNErIeGTEGLpFhRpKEelY/3xcotp7DCXf5SXn8NIxXk37ULfdGJK0
rT95hM5igEAVSWRiFO/s1lM2EppFE50HKV+KRjGeYMA1GTGDl0pdxZh6I1hq
m3JUZtcMWgSZvdjaNoyjR5c3sf6dxnYf8yeEw8P4U6euTF1uGr1iJAeuJ9Fw
I+vFp63pU/gwIjcq5C4NOUP40k+emsL9Pk9edwoMYdRfmk2F5ZNYrmjQ50Sk
4ifNXTH+BpMY3j4Va8CioENi1P0wygRKMQIdWakULPfPOtjg8N/PF0EaG1cG
0PhT9s1DHBNopO1eoGA0gG7EsYNJb8bRQtaktkF8AL+u/5ZSlh5HRdk6q2XX
fmRkalqW54zhgxpj77f2/RjxsuzRFa0xVJD9bHJMvB+NDX0M2qmjWF33Q5s2
/gubvFeNz7mOol2FZUhJ8i98bPvpQqjAKAqzRX3Hlf/bS7YrFCWOoOCYHNlx
uA9PGeQ5FxBGsDX9oYPnlV5M+UHu8+kZxpo1b4lZ7V4899zJcofzMBL5TQnf
jHpQpZymY7VtGCMr9LYJ6PegcgJbwfYbDeUiQswaw7txR2pQieRlGq4O9Wnu
e96N/uNS271HhvBu7I0L9aQuXCK5GAV5D+GZqs5nFWmdGNIWvH5s/xDmi/KX
63h34IpHe9Lj0kH016uQ7nDtQNIQSfqa5SBuCX5A5fi7A7cq9duWcA1iOzn/
+wG+DjzkZ/4xN46Kgw9M9b2n25EnYX3r8YtUvJ17e/55aTtSrewOnhiloIn9
Q9qIcjvq3+bwz/GnYI21FOmiXRtKZ89R0hUpKKH6hK1c24pBj48JEWIGMItF
94gRbsUtV2MZnGP9+OXGkSAobEbBfvLzf//qx115y/WHdZvxwwf5/YLuv5A/
yVTjyJlmDCZnWOmW9SH/zqXMsK9N6GjTuOmKQB+mi3nszhZsQt8YiTVhk168
q/RviNJUA5Jj+W2CE3tQuE+z28m6HpVUQ4NyWd0oEcImPuipQeL5vZTAc90o
2WdgbBBQjaQrAQsb3nShgd6qI+teNRZOKYXsonRiqfD6iJN5Fco93uNfebgT
3QiOvRqJlUhJPTq48VkHGriS5asmK1C5LCa/sakds/8s+0pWL0f9e0q6ElLt
WBL+8LLH32XoKtK8OPOwDdtcTiZTWD9R8BWnwsmKVjym6KhFOvETX0Z7Oy2K
teLabt/7ReslGCWz8FDOrgUFuWZ/qxeUIEvBZ4KMzXiTGeZ76nsJ/rb/8hmF
mrHSeh+PNakEK13mAvfaNOGtntvS4saIT5tL5TPcGlE5Q0dl/UQB9kY/ed28
vwHVDtiTWHZ5SHwi4BneUIcrzZr9T1JyMe5EAZHuVov+MtE2giPZWF+8eqtX
pgZJ4meViO7ZyBESfF2rpQrb9r/OnxTNwIqO+7UnPSvRoVbEelooA2Ml1l2i
FCswxslahbSYhm8SDh+51VOGenqyTbWlKeijnNgX4vcTW6KG3xoUp2BVCpeT
8PFSZPW6aTWufcO4c6JLI8NktNdsP7Zv7zf8tuHxtnV5xGwupZ8VpK8Ixeo+
yX6F+NbkEttROBkzky6lFI/mIbg5/Xn0VAKmlmgvymvk4MrZwx8NVBKQyLE6
3PM5CytVhPS+P4zCv7tjucibMtHLXRLv10Riz7WNVa/rU9FTa6XjllckEi9f
1yoNSsKjOzrGXLte4RfVlCaWdjxy/F8qsFuWd8/H/3dO6QeRH96HocdbxoFx
cV9QVjONKVV+jjrtlS3jnH5A2dmlKuZ5DTZf/UMq6FIA6CXeqzzb+RJ4Zg0v
138MAPNp321Mx7dg95fjnBx3MLBdkomiHjEQk2N0xq/qDThLGx+uJyeArOof
X5wkI8ATJrqLN30F59Ga4l6Rf6CMc5PIZrl02LUQfK6hPBro7Pg4p9pMCKKe
sX4+Hw0E6+eaGY4/4DQ5ev4kfzwkd/y83SGSC4u7RqWpNglwQTnWk1WUD9+K
WsVJIcmwLCdO3Hu7CCr5FYM/r3+DmK5B4+88ZBjd1LJ+UTANVBb1bOmmJaDS
2dotdD0d6hXfcjdllkKjVtAp9qUMoGnmMk14y2CHqIq60N8ZoH9SWu6jRTn0
XtaK29KQAWe+/0qNya0Au9VmvtAfWeD/uaTkvmAVFM59yEjm+wG24X3FAveq
YTTGpe1CRTa4OXQcflNeA5kvh45r3sgDop9z7YpkHZznI/BmchUA48gpV7Mn
9ZAvlzh90QuhYEhYt7inARbupMU+8EYINt2jG7GnCc7zos+SJxlaDmyav1bX
BGGnFWgZx0rAJkp8NcmjGSbCeI/X2ZSANKezdfifLTCy+cIPzakSWKDzaO8Z
aAFbSVH2fZNSoI49XtZ40wrrN/33t+7/CbZ6823iF9pAJ0xcWOBSGRzV4b0X
v9AGHCb+bnVmZbBXJO/h4Nd2YBm/beQ+UQ4n7d839Vt0QNRck3R9ViVoEIVC
YkQ6wbv8jrxhQzVgQPLsofpOSDdVLD24uwZ+cAaav/HugrpkebUXaTWgKi/5
rPF0N5QZ0t77GtcBfWfjIQa7G6rv1mVdqG0ELfeJp2tpPXA/KJDMsmoCB+fS
kvW7vWD0hcka5GuG3IUxv1XZPrhSd9N+6FYz8BR/TuKg9YE4TPMruDRDpdBn
wvbYXzCv6DHj9qgFIh51/lC92Q8afrFz8j4tkJAYTvbdNwCG01IuD2ktUH2N
x251cACsariXUg+2QoP21NZ2Awp8DQgJ8I5rhRvkf6pqsyigNbVWL1TVChPe
XK42olS4Y6KvlSvaBjwedwfT3akQwuPu85dnG/BFX9/4tZ8K5Rvl4yK6OkD0
+qiY2flB4D/lo8G52gEvAlXC6r8MwoxDaHiEVSdslT+kyC0wBBHBXExXt06I
f/eSuoE0BNQpr7I+UhfoE0R+d/8agrMn5E1PJ3ZDvImTwCt1GqitCLvLJnXD
IcXlzeLpNPDoyt2YONYL98xPKrzfNQxfz8aK15ztg3J/FNvqOwydtQMmm4V+
gVeHY/fjuWGYjS68ZtH1C7SlzKj0GyNQycdR2q3ZD4quCmKkhhEIO2MlO6bV
D+8t5Kk7zoxCy2djiYuGA3DuqYB0b+ooRE50/PPBfABc9r2+1iw5BjscJVzz
RSjgyIO+G8L/8wKe8q1uFGi//ey21+ZxMJmH6CwPCvTWLBoZPh2HQkZXpHQc
BcJkzj4OZo/DE+X47KlqChTyOhSp2k+AlY7XjQJvKrwjSI3bjU3AdLS1WFwM
FVxEK3OPWk8CX3OgsJbRIKjNlU18pE6Czr5pPoV3Q6Al3W1UZjEFRadtRCyW
h0CEZ4wvhzoF36zMzxGkaVDNF3Uz0HoaOpt/bNaSo8Hq0wP7TManYerqs6PZ
J2iw1bQhVtVxBp5dMN0ddJkG3c632BpLM5C73JLrkUsDF9km3mjvWeDMPDGr
dWcYKBrzjIO8dLD1B/fIZ8NQlb04pqlPh/xbGSMCOAxiL/81xCg68OcRLStr
RuBDCIPv/TAdvA70EAvPj4KNiNyDuSMMCLH5/Mk6chTO23on93oygOSnEha1
cQxY41qt9o0MYG34+Pld3zjolEqrVkjOwZTSL5XQqXEYzPBJXXs4Bww1TQu2
zARYW+nUHq+egx7hjKLzgRNwJXjOKlySCTsVEmKcZyZArcCZdcqdCQU33521
4p+EV/qH/7zWwQQMKvq5cWwSRDbYv9uhwoJ+T62lVtMpUFZ5cTP1LQv25Brx
75iaAub9tIumv1lwkZXOPqkwAy2rvPmWVmxIOWVLEjCjQ6fOTsM/GtkQZsk3
qvqUDqz89tfZZ+ahcXue3UwuHbKotEXMnAeduUcjhZV0WMzhXP+osAABJ66l
FY3SIdv9qm9v0gIwrxJlzc4yYEukd+iOQ4sAfR4tAT5zwJqvdOTLW4SwYDPP
Um4mTFzV4owlLkHYoBOXkzoTju2J204fWYLncZS2q41MUFOVIOoELsO52Srd
IGDBqvCVTfZqv8Gw+RJP9VUWBNsOKz5e+Q2HGFTF7blLkCJ9TkivbgXEAwLj
+bOXwUZq1rwqfRWEuj5XHvVYgSxfAkkrbQ1mktqPh9BW4FQ2Jby2cR2S6ze6
mLzhIIBod6j+aw4C5xq/fwmTg2CrYphmacxJuBqSjNRlTkJZ3vLQISMuQsQm
JX+SITfBr87t494CbsJzCyemfcsWQo76mbhwpU0Em4bLl6yCRAn/A1zCWdo=
"]]}, {}, {}}}, {}, {}, {{}, {}}},
AspectRatio->0.6180339887498948,
Axes->{False, False},
AxesLabel->{None, None},
AxesOrigin->{0, 0},
DisplayFunction->Identity,
Epilog->{{}, 
StyleBox[
LineBox[{{-8.62501550382003, -5.485558191362114}, {8.32555754281431, 
        5.303705637831441}}], 
Directive[
RGBColor[0.368417, 0.506779, 0.709798], 
AbsoluteThickness[1.6], 
Dashing[{0, Small}]], StripOnInput -> False]},
Frame->{{True, True}, {True, True}},
FrameLabel->{{None, None}, {None, None}},
FrameStyle->Automatic,
FrameTicks->{{Automatic, Automatic}, {Automatic, Automatic}},
GridLines->{Automatic, Automatic},
GridLinesStyle->Directive[
GrayLevel[0.4, 0.5], 
AbsoluteThickness[1], 
AbsoluteDashing[{1, 2}]],
ImagePadding->All,
Method->{"CoordinatesToolOptions" -> {"DisplayFunction" -> ({
(Part[{{Identity, Identity}, {Identity, Identity}}, 1, 2][#]& )[
Part[#, 1]], 
(Part[{{Identity, Identity}, {Identity, Identity}}, 2, 2][#]& )[
Part[#, 2]]}& ), "CopiedValueFunction" -> ({
(Part[{{Identity, Identity}, {Identity, Identity}}, 1, 2][#]& )[
Part[#, 1]], 
(Part[{{Identity, Identity}, {Identity, Identity}}, 2, 2][#]& )[
Part[#, 2]]}& )}},
PlotLabel->FormBox["\"MSFT\"", TraditionalForm],
PlotRange->{{-2.87500516794001, 
     2.7751858476047704`}, {-2.8523556428167356`, 
     2.7184936616092057`}},
PlotRangeClipping->True,
PlotRangePadding->{{
Scaled[0.02], 
Scaled[0.02]}, {
Scaled[0.02], 
Scaled[0.02]}},
Ticks->{Automatic, Automatic}]\), \!\(\*
GraphicsBox[{{}, {{
{Hue[0.9060679774997897, 0.6, 0.6], Opacity[0], Dashing[Small], 
        LineBox[{{-8.694948115378702, -3.0278639449241225`}, \
{-3.4015357976266287`, -3.0278639449241225`}}]}, 
{Hue[0.9060679774997897, 0.6, 0.6], Opacity[0], Dashing[Small], 
        LineBox[{{4.015701989439402, 3.4662317887317755`}, {
         8.237675916947204, 3.4662317887317755`}}]}, {}, 
{Hue[0.9060679774997897, 0.6, 0.6], Opacity[0], 
        LineBox[{{-3.4015357976266287`, -3.0278639449241225`}, {
         4.015701989439402, 3.4662317887317755`}}]}}, {{}, 
{RGBColor[0.368417, 0.506779, 0.709798], PointSize[
        0.007333333333333334], AbsoluteThickness[1.6], 
        PointBox[CompressedData["
1:eJw9kHk0FAr8xcfSK9UrRVJCQhpLKK+M1FdKSK8QL4Sk5GUJKaEsJaKIV/ZK
RMkTWZ49viNL9mXsSzRmbMMYY+wTfv3O+Z3fPeeeez5/3HPuuVK2LsZ2vAQC
YemX/ze/QJ4RWXk9+ZTv1RJB0gbyjWwbnCvgJyd+kvL2kdlAvnTk2cMbJnzk
a2zfNfVkPnKryJj1oCkv2dZM5J5KHB95q1B+BX8YDzkvamH8BJWX7BmaY1U9
TCA/S/afFTImkP/yzRjLMCWQL8wl6Df4rWHlQ7/CPRlr6JlrtI/fZRV5dGou
D9WsYvGOj661jBUcNCQ26CytIGnuICk7YwWVvnW5OGms4PfwF4F+7itoPHK1
8EHIT1yt+rzLUZWL/UzKRQM6F0vCTuy5qcLFbNo2Szl9Loom3fpSrsRF4ZOk
4ML8ZUzQ3Ow2tI2LX6sMTMcUllEog/Pel8BFpZb9UpTUJRwNe6vQ0b6M4nny
lALiEjJq9SfpGsvo7iAYsZS1iO8+1uV9+NXL2RT0auvxRWT76vknyy0j563N
+8DGBdQ408GMWV1EzzZNjYWrC3hn84mUD8oLOBfRvbh5eR6zw32YmRfm8YCF
6xXvqHk8zHO6QOz9HCrKH9n08/A8CkeGkahv5/DdfrELf3XM4YyhKLVk7xyy
0o9uMfGaw5K8l4cCBOdQQ3ZvfZXkHIodHSCqiHEQ3myl+tfMIu3BZ6kwzgwG
qLsNWLvPor7knawPC2w8WXVyWXPvLDrso5k5d7JRIUPtLbeJgwSugaJ3DRs3
FSRs8PXj4BVD7frl3Wx0f7PCTFPloN8TheL8zWzUGonWsB+eQanjOv7k39iY
s12u+W38DI5IihFZb6aRqrliAEYz2FMjIHDcYxoZB5SGDgnM4NgXN6WNMyy8
9gblb35l4/HJ81lFQSy0VlrmpTxgI7lFLd7uJAs7Yc3JWp2N0Zd8ffXWT+Ej
Obk7hLlp5DrLex6rZCKfbJhwes40xk2ETC3fZOIDNxtZY7dpXDdi42mRP4mM
4Xgdhso0xpLEukd+TqCkV3xU6xALy6/uPHfLeQJjCryuPbFjYeYj65N+thNY
IXJIijY+hUMyBHeSzARmhyrsaHOZwvcrn0vyNkzgqU+PQs4sMHFL6fpTDT8Z
qPZssEDJn4larwRGwxcYOGCvXuC1kYmT+hR2+HMGtoTrOe6JnsSFm4Nj1O0M
zCA9u7tBehL1KpXvuUSNo/mBCDnV7Al89tK/423AOCarBno81ZpA3fV3tapI
Yxin187a0MpAuTX9XQKcUYz+pygzyZaBxt875E9kj2K7XaHx2blx3Pbqaict
cRQVdvbMLwaPY4TZn7qOMaOo3PyKmCI+jq+PHd8fHjKK2rvDh7Vzx1B1wmn+
C3cE0994P23QH8PjJNuf5KkRpMsJdqlTR/Hy0Spzo5QRrK0Sofl5jWJ6yXxt
tPEIxrfz747fPor8H+32ufCN4L6Da3/4fxpB5hZ3KoEyjD3hascUdEew7Fih
I9FkGOO1w9wjh4YxTLAp+Ms7Oma2pTrk+Q7jqSxp6fSndJS7vofxRGwY4+gn
iadN6RidS5hfV0RHw9nolfR9dOyPS60lXqKjs1tYslo1DfWlY9qZczT0mki3
fe1Ow0ZOVsG5KBpyKgSKlpuGcJgbrH3yDxreVw9QOF0+hAeHR1yrO4bwnoae
Ls+FIQyauvV3l8cQ3vHYkPVQdwh3k1w8XESHUKqQKd0uPoQWdU2/Py2mYspG
1WF1FhUPfRWr2mdFRYL+Sn5lJxVJ9/NN/iBQsXD4n0OSkT9w6/2dUaXJP1Du
3p46WbMfaKRz0KdA9wfSEkVlX+8fxI0xmSdPdA+iqeGBdA5xAM2zm6ypUoP4
rC3YyVtqAInTUXRDpwGMmlORDDPpx8/jrjGBBd9RuWnTRRlKH2aajjh48n3H
E0acdGvsw6C54377DPtxmJ6w92hhHya+0JH0edOHciI8lI7UXlzefKjs4UQv
Gqy/65D1qhcF4uLniBq9KM8NeOLt0IsTt0IDXEJ6UE5gS7K/Ti+SzuXpnevp
xlgJlaX2g71Ydib5TDGxG51D1dPK3/VgcbBoQq53F261eqR6JLYbq1Ldwg41
dKJSYgvjh3k33rUSd1GV6EQxCwVjBYM29PGRKfzXtQNZkvs+LBF+8c7y+diK
duyp+uA0/IutK/la50Xa8ZballsdZAq6HgziQ4c2jGyc1W2+24qXZog2k2UU
PK+2LS+nsQU38dMavIQouGejYzEpuQVDm0O1bf9uRbNTqv6lJi0oZVZbn1ja
gqsv9Z6dP9KCF5PHA1SEWnDEMJf2orUZX4SWKuyiNGHk9k8vMjh1KMOw87Dx
bUQ7jbPPGbK1qDEv5KGk0ID1l0+xtM1q0GanEcWjuw6P/kXK99KswR3Id/Zw
UC1WiHq9Whj9hulHorPN1WqwoUJ5b6PmN/xzTY79Y6gabT1f8ubrVKNJaw0v
+Z8qlCapfRborUDvC1+mmVqVeLfwZpZ8fxmee1bVdnX6KzpYSAQ4WBRhvq9X
6/bEcuwyDEkWdM3DiPcxuxcvkNHIp/904u5cbG9spmwjlOGC6ULmacUcFFyv
QfCyKcFi19q2Z7ez0fPx3fPC5YX47V6Ozd7iLExVWr1EkcpHSlJryWDCZwzn
f1Wa9CgXg2VvO2lDBjr1HZV2o2VhGJE5NjiXhgYCD82tgz/henGe9sreNBTn
X5yL1E9FhZiw69TgNEzzaDC8tvEdqo8bFV/u+YiLC7tF/4yKw2Q+qRNdA++x
20r069SB5yjpmKyoQYrD6QOfNVZ0byNFMTTmamE0uloRrwfV3oOCL4ESpKR/
kHDjFnHGMwL+EZhI59sVgdMd9q+XeF4B4f90pmayebD63f8zP+Od6pktH6Fk
a/paAOkFaBt0G5tcygD1jIDFEptYMKCxXXcaZYOt687ZHuHXIFUf5eazkAtJ
2bqJ948nwnpBnf6phHwozb509f6XJJB+7Brpq1sEM+FXLJMsk8HuEisX2CXg
oALbJkPSYUVt5bnO6zJoUufW3Z9Ph0d8Cv1GKWSQeNAWIaCSCRI/CnmPcsth
atyeXb0jG86Zuen3G1fAO0Hxg1sn/4MDj53oBumV4E/60CpunA8O8qPKEfzV
IK6er5d2tgBuzGfk5Fp/A59t+s70E0Vgkf92b3lRDVTIWp/WtyqC6bN6VhU7
6sAFaUqrk0UwsDnat+p2PWx0I65MRJXAZHB6M6WlAYT/vWLfaFEK/S+b2+aV
m+CrR4CIqwAZtHt89I9HNEO3Yrm6tWQ5lIs0ivR4tgB/g4ria/WvkPX0+qCK
fCs8Pce64BNYDWaCnlqK/a1QHCUmuu1jLZDcXRNbn1Mg/nJUUJtYPVxvEw2V
024DLmQOXRdoAHv75EK1+TawKnY7/yK8AQaca9YR0tvBqCRg3Na8CbYo8/hH
2HTAmW+WrayaX7uEqbZMkU4YYDr6MQWbwWxDuJhEUyc8IBK0+s63QJf7VQP5
oC7Qcy4/JmbaAjJ33tbtgm7omZp0zuRphV28Dumzi91QP2a5JBfcCs7bWzQr
cnvg9LZc17q4VmCwBLc8d+kFytDnvWd524FsIThjpdgHnkrHLh52bwdhPQKf
JqMP3OaXz/IltYPv3dMfVNP6IYkkv+c5pR2M7SIj9G5+B3G71TeSF37trrSp
eyo/AAd/OyV4zaUDbmU//I+XOQDnSvt5bCU6gU4//HtJ1iAUflAxzPmzC3iT
87wHNX6Ag5Ysz3dGFzzZfpK7OeEHNB/03Cdo1w0eD/fzT/JQ4Y5ZxXpWVDf8
19RY/+gGFQyEuCJ7jHtg1Sm2uqueCt96sgYWU/rAXSjhX7bqEGTty+kpUv8O
yfxZ7l2xQ7Dfp6w1JXoAyDfS7CMINPDucsnb0TwAgf1CYjI3aRB3YHPq6OIA
SJgf8Iin0GBdtMla4qZB2LTlj2KuJh08RIJD7VyosO6v208MP9IhvSOlwWqc
ClkpRrQk4WE44W1gG5Y2BK4txrD0cBgeM4Yz0lTo4P7E2d9mehhucd+4a7vR
wc9VYv3QlRHQqVInjqTQQdWeWBjcMgL0R60fSYRhCPGU+c1GexQ0ewL4qNRh
+NRE5brnjUJbnRRB8tDIr99adVuJY+CW7HD1vucICNZ56gW+HQNekYkfnetG
YdeE2O4EkXGgv83aF3pmFELrK9/Lh4/DEbJaZu7IKLw1rc/WEGAAyVztvrT8
GLjOb58deMwA3fpPapnKY8AtOLyfyDsBOn43LM84jkHWxmYxxYcTsH+PZKNL
2xi0S1n0cXkmofHcaYLapnGgBecWZTyehDiZhadHs8ahL2zU00yACR0bbtZK
lzAguCzGQTiCCaybHtuOzE5AbFxYNFd0CiyfHFTgBDMh0Ut0hJgyBaV6ERcv
xzEhK4JjUqrKAu2Iv5X9vjMhofDlgc5yFjiuUdxN6UyQyHGPMZCfhg2hrPMW
vFOQGUjjFbo7DbGZxQX0e1PwXfNsvmn5NNwpDZquuM8Cz78mWohb2TC41pGc
EcuCuHMP7VOt2fB4y4OeNe9pyLj+/OvYZzZEJGx1C30wDayu0g8b+WYgsPKj
poIlGzI0LdMUzWag+Mn0S6unbPhQ6fTS7fMMrCnY619ms8HS4HHn2gYOrJM0
FYzWn4HN1fY7ee04oJTkmLn0qxdX+6gttYIDyzwW7tJKHIhe+iK3X3YW5CJ3
3Dh2lgNXVGTLC0NmIchSaeGjDwdot0N4k9mzcCJtoHHcjwNXIcNZ1WoO7gnZ
VosUcEAinXKtpGEOjik7hdiWcIAqYGX2XmseZEMOSzPuzEGIyb34a0XzcM5a
tW7/yUWIcnEf9zm6AK5ht9+dv74IKnax4pElC1BQtlxy8tQS+P0INLx+ZhFc
o+pScv5bBvEAa5m27kU49NyL94zRTzgbJrlnwX0JrNJsvx4O+AllgZn+B3Yt
w4kZlcii+p8Qe0NGXbRuGX4GH7v4VHEFdKfvRrKDuUB8QNzh+WUFHOjCMs/N
foK5JSVm9+QKqEg1+NdorsBWX5NnfX+ugtDr1Lj1x1ZB4ndKmJ3NKpgXZgeo
X14DkZTtgdc2r0G1bX9qrwlBy9fpv2suwgStRze2nMoT59EieahrOErza20O
yrbT3MOr9cEqflOF1DqtbTxPkuv9+LR2GFL/DVPcqGUX3vdH9MI6rb3p9iVd
xZu0/geY/0FW
"]]}, {}, {}}}, {}, {}, {{}, {}}},
AspectRatio->0.6180339887498948,
Axes->{False, False},
AxesLabel->{None, None},
AxesOrigin->{0, 0},
DisplayFunction->Identity,
Epilog->{{}, 
StyleBox[
LineBox[{{-8.694948115378702, -7.662463419291668}, {8.237675916947204,
         7.162743031508085}}], 
Directive[
RGBColor[0.368417, 0.506779, 0.709798], 
AbsoluteThickness[1.6], 
Dashing[{0, Small}]], StripOnInput -> False]},
Frame->{{True, True}, {True, True}},
FrameLabel->{{None, None}, {None, None}},
FrameStyle->Automatic,
FrameTicks->{{Automatic, Automatic}, {Automatic, Automatic}},
GridLines->{Automatic, Automatic},
GridLinesStyle->Directive[
GrayLevel[0.4, 0.5], 
AbsoluteThickness[1], 
AbsoluteDashing[{1, 2}]],
ImagePadding->All,
Method->{"CoordinatesToolOptions" -> {"DisplayFunction" -> ({
(Part[{{Identity, Identity}, {Identity, Identity}}, 1, 2][#]& )[
Part[#, 1]], 
(Part[{{Identity, Identity}, {Identity, Identity}}, 2, 2][#]& )[
Part[#, 2]]}& ), "CopiedValueFunction" -> ({
(Part[{{Identity, Identity}, {Identity, Identity}}, 1, 2][#]& )[
Part[#, 1]], 
(Part[{{Identity, Identity}, {Identity, Identity}}, 2, 2][#]& )[
Part[#, 2]]}& )}},
PlotLabel->FormBox["\"FB\"", TraditionalForm],
PlotRange->{{-2.8983160384595674`, 
     2.7458919723157345`}, {-3.0278639449241225`, 
     3.4662317887317755`}},
PlotRangeClipping->True,
PlotRangePadding->{{
Scaled[0.02], 
Scaled[0.02]}, {
Scaled[0.02], 
Scaled[0.02]}},
Ticks->{Automatic, Automatic}]\), \!\(\*
GraphicsBox[{{}, {{
{Hue[0.9060679774997897, 0.6, 0.6], Opacity[0], Dashing[Small], 
        LineBox[{{-8.557314213621972, -3.5981403826688174`}, \
{-4.556517431185752, -3.5981403826688174`}}]}, 
{Hue[0.9060679774997897, 0.6, 0.6], Opacity[0], Dashing[Small], 
        LineBox[{{5.015626009030535, 3.89671083743314}, {
         8.567038225661562, 3.89671083743314}}]}, {}, 
{Hue[0.9060679774997897, 0.6, 0.6], Opacity[0], 
        LineBox[{{-4.556517431185752, -3.5981403826688174`}, {
         5.015626009030535, 3.89671083743314}}]}}, {{}, 
{RGBColor[0.368417, 0.506779, 0.709798], PointSize[
        0.007333333333333334], AbsoluteThickness[1.6], 
        PointBox[CompressedData["
1:eJwVjmk4FAobhhlUtlMpHQkpSVJRlpTyTuLYsoQSR9RRSVpsIUtlCdkSUSlS
qRQtlLK/Y1+zjGWMbQzDjJ2xjvXr+/Fcz5/nvq9nx3+3zC4TuLi4OH/y/1Z6
sV+4pnENidCq2LRcKUQyXnWRoJrxkmwcourt+daRlDLU1E4OE0g5+8o/9tXz
kUqydXTbB7lJDaZ2IhqFPKSZ35a3c6S4SW2si5KcTwRSj2uETvxtLlLUC02n
f15xkc4reBCzK1axdvlUz9b5VUxkSO57Vr6CcRviW93frOL4/rNQSVvGlFSb
+Vsry0jrs+ttFF5GIXf5I4yWZdScizOpP7WE0RlKvFHrllFXpjSr+/kiKq9Y
5pr0LmI+5cSdOvYCchz9GiO6OejFkvrNOrOAyeNH19Rnc9Ce3zegsYiDjAjl
drWoecTtAuM3VTm4Wj19yVxgHsXTBqnUr/MomtYVoNszh3KnnQlmSvO40fyF
FdF9Dm/lrJJUf86hfK61SN7yLIYmVNYuEufws5K2XE3pLDqOeD840DCLviU3
Fr5tnkWCdbDFVftZdEv5Rwh1ZzBO2a7DdGEGT1uPXv55bQqlab65CU9mkKys
4lVycgqXHuXXcB+aQf3wV+tN29i4ZnRTlj55Gq3ti/0LYtl4fNN7PHZ7Gjeu
vWbfdZuNi79tGZ/Ep1FUapuplzMb5Ws7CY7FU6gXerhV6yYbt3lvO2p6fQq3
WMWdG1dmo2qRls1xsSlkv6JFbnKdRBm447WhnI38ItGTyRsn8VbjV4/0P16z
2qgAr8kJfHdapXh2Nxs/C5sUUhomMDzpLheFOokSpnsCLxhMIF1egawWNYl9
5Ajn0b/H8bKt90tu7UksoE0pCd4bQX6+Ratdi392+l7iGeIj2GOq7RL5fQK9
CxIspYqGkSbVGr3vxgSKuxr6b8wdxk2Cto/YchNo7VTIMi8awtyi+6/eVIyj
xYVFtc9aQxjim2/qeWIcr7q43NOeG8SFEJMEg4IxTJC0Yq9xHETGR1UvPo0x
3HY0hHKFysTtM7mWMbmjuEH6RaOaDxOHFW3nOzVGsVc0dpeiDRMl9YdNyIUj
KMXJtx04wcTC7Y4uF06OoJHJzw0tCwMovRLo4VE1jO8ZuTxPRwfQdf1eJ97T
w7ga9OqHsMcAeu/eqrFIHcI0iQ5GLt8AlmbJvj51aQjtfIcnWF/7MWK7gNjw
+CCuaVnJMXrUj7Y5sbVVvoPIarnb2GPUjzGH1j3uFBjEhIf5XkIa/dj36k3j
3wksnJelxphWMJBmJxjmvJeFLeu/3X0Ux8BZ9wyNzjwmdlyd1ufmYeC3/jGG
qTETN7tHhqp09eFhHcZ8KX0ABQv3bci50Yc6xRxLxT8/h0rSCib8ezHur1m9
EMEBnMiNz6ETe3FaNtG19HU/Jpm9wyM1dFz1qW7pVu/HXz4PSgMC6GhwdbGi
roGBemtuzvVdpyOlEcYiHBmIfs96tljQsVU6VF3kzw+xsAO75LToeOCyXpdl
Yh92r+d7FNvWg3U3HM9YqvfhsH7b3QlSD1K0/M8JNPdifmDfmFtYD3ZsMaJe
c+5FdmjjGoegHrxk7kBwE+7FE/xPvPpMe1BnQEVZMo2O3Vu/qrLe0/CVA9+y
vT4dmTmlXGaHaDj/93/SWqw/nFsW5u+hYenG0LDMkB5kWgWJSKZ0Y62NgPk3
uR5MOl/+RMGwG02zD7rdiKah422XjcY1XRj5jqwbQO7G5fZLtJOVXRg0eu9w
vGg3Evb73S+X6EJK0N6EZKsufLLi5i4y3In+5Z/XPU/qxIT1bxQO1neixodA
K09GBwbrF1+KP9KBVakfEpUVOtChNWk4aEsHyp94J1nu2o4kb5ugYIE25Eqv
OyuXR8Wq2E12300oaGH1fN6El4orW8ZfKB+g4AN7yV514zZMnLFw0KltRZ6P
Wds7nlFQcoNha+lwCwabF7IUGa2oqZs8JO/UgjWkW4lKSq3YI5n7VESiBUMH
mkpbfVuQXOz35XNEM0bdbBaQqG7G0gaCqxS9CdOZdpoLfzdjUpKYlOrLJjR8
kGLidKUJ32Ys/Dp6sQm1CXbGjllkdD5Q5NlGIaOBxbGrY7xkDH1y96GzBxm9
p04xpy0akVvkwfS20kZ0iQpV8nzXgMK1JB1L40aU3lccRBupRwOzSzw8Gxqx
VqPySuajOrxY0Xbo+eEG1Ndoumij/Bv14+7lmefXY4Bt0iKZUoOu7mkx+1t+
4yLDr1fQrxr3lAUfpdBrMDyeMLy0swrvZncOO1NrUNIzQ/hlVQX+5XVB+Nq+
KqzXrbtEcy5H1bIZZb4vJOy7e3hvgVgZRgu8K3bdR8IxF7MshaIS3Cif1n5O
uBCv+K25s+NaMYanU5wKD+RhB085d9ymIkz969FHp5ps5FjqMTneiPlCOnZW
478w7+3IhuT6fLxonOgzEPcD+8y5JARkcxEyNC8PaXzHME3zSlmfX3jQzS87
WyITk5e9Z3saf6B/qp4zz0QGmoheSJGXz0Q+HuOrh6u+4VrrzKYO7q9YrOhU
qiPxGb9bvhs6nPkRZ0xldv6cDcLO3YSN2vYpWHEjSTWsxA0qllyac+ST8Kju
h9PT6p7Q0Rx1pTAyFq0ePcyJkIqDniH5ySSGP96MlgnpfR0Hu3mK82MjrUFW
ef7JfHQiLDlZ9/CEhkKuuKB1LCcJQFSu25kWD/tVNk9UL6ZCvBTf7p8FySC4
+dbrD/QvwPmn7pSk0HtofCxTIrfmB/R7uuze+G8aGBZ7/Bdd/QM2HccQ6zPf
4KVXRYnm5V9gJ/uPVvxyJmT5MKMslnIgV/jiE6P3WbD/cA/hmEo+PDc+ciXG
JBvUpVkNnlAIy/YDOR6cXCiISJe33k2Cou/kL0IpBZAiciqxyJ0EvCpPtb7L
kSBc26koxbYImII5pjV+RcBrWX99vr4YbjzgVFg2F8PVsr7HDhklMH1Hh/c/
hVJoq+F+45RcCuPBe+9MBZSBUWMBUzS1FFpNir6LdpTDFl1a+HmVMpC/l2JD
Vq6EoLulauvSKyEyaeaIcmQV3JGR9pwrqwTCqPNBLWY1uGZ4hTusVkLUlccG
/Fq1kOQWv6fBqRpMT5Z/i0n8DbIPn6lavq4G8sm8LBanDuw/cilyLdfAloT2
wTCFBgiRpWsKmNTCbRHCuZj2BjhUnfDI8mUt3Pcs/2tDWCM8FrU+71NWB4Zt
WY/4j5LBh+e0rah6A+gGt90OGiIDZcbASrejAU7zS3kGv2gCPvE9JhkmjfDV
iXpZ1KgZaLangk/+boQYttGhw6vNUKtRvbNgMxmirhmNTGa0wMAuifM8mmSo
1x4sNbzcCuwQIcHrV8gQQTm8wXArBdyrIpNMvMnAu19Rd/Y3BYQza6JUHpHh
ITOe3yKwDa4/5jG+RmkC6y4RaacjVBAf2x1f2N8EPEp6d7UmqLBavVfPdkMz
7CuT0qF/aIerm2s8XG80Q/2+HWXGFzogWCXyaslCM2gqLN+P2doJHnaeav7r
WyDEQE7pR1MniLyenGzNbAHKupSivKguYOUGqj2/3gohLhzbDINukLx3vEtK
kAKx8qduJa6lQecLn9y9mhQwP5aWEFpGg3mJOv+s5xSol6oYOK7VA+O+ZZW8
m9ugsklbivimBx7wnY5239EGC1SpH/UEOnAb3vfeZdMGb+WLoyft6fDcT6L1
wHMq6KZOln8qo4Ndg0ydaioVHER3xXPt6QXJ94oS0uVUoLXx35gP6wVL7oBT
7WwqtPNqjjwd64UajcqVAOt2qFfcPcgw64Otq18Tnzi0wyE5Ppf+X30QNTJy
Rk62A6i92rWvJBlgM6Y8+sapAzpil/zFgxhgsW6IrhvZAYZ7s/+1GWaADO+Z
hxNGncCtGeJ43bwfWhYiSUPZnTDPtFpjlt8PZ2viwqsGO+FpQ2bn5t0D4GhB
ct9D7AH9oJ/D+dEDkFlkIRkmSAeNta8jzJYGQONZ5SdbMTpkfkjz6r7KhOqO
MtEfZ+mwoHaz3rGVCemqk2urzHuBvqNSckWbBX93FpNnenuh/6Ld5Xc/WJAU
IFzVvqkP4qdLd12THYR0j/JDRB8G2PmYXrB8Oggxp3y2yq/th2h6eZqXwBA4
zFzhrZHth0rPXpX2u0PgZhssduFyP/iyWupCp4fgwB23FWJMP3g0Dqw8dhqG
x2EN7VkqAyBFIgrwMoZBlHPWX1lnAIrosnxj50fAMtxcYVqGCTsEU/vsqCOw
wr+nvuEJE0YmxSOunR2FxPx1pfYyLJD55Tm8vWUU9mgkbZsyGASWE1sw9swY
bNo+ZDTbMwjL+kIH2ihjEJVdn+bLGIRwzTsMXptxqJGr3jkxNQg5gceVlXrH
wXB2WoFgOgSbrx+zOqI6AUMhrdpTzcNAv/fD2s17AvQy9oiUGo8CPWOnRjNp
Ala/LAgxY0dB8ApVxmndJNTF73D75TwGDnjuit7pSaDRrzbyp44DPYz/pd+L
SQi+v03i+x9P5KpNtSRzEuSNRSx17k1ASqZIxHEVNtwykCrI8poE50NRxKkA
NpQbPvMLVmKDbLKllmUTGwISi/hNgA2qO3fsDpKdghCqWGaaFRvEOzg8T+9M
Qei2oS0H77BBYX9e7df6KbhoU7JVbNcULB44/mVSbho8E/g6nydOgaZ70MPA
gGm4l6rinCQ/DbzG7LvRtGnwD8zP/fVxGpYnEuL0YAaOVkurpd+egZ3Ef4Po
r2dg4SQzMD50BmKfHH/3dO0s1P2SOhpNmwHuvEtSX51nYW1nVLnx8Aw4GVmZ
3O6ahfNfPvF+EZmF0MX38VrGc9B9vpBLznsWXMS7w3xL5uBfdYMTXmvnQC7T
uPbZ8XlI2ETzDOefgy1ClW+lC+Zh+bWw4rs/XNF9VnaWFgco6lWBHNI8/HfN
+pRYPQcMq7TWs1QWwEt/OV7RfgFmvVLOZzstQKG69ElRrkU487ZGPeLzAugG
vbkn+2ERiH/p8jwmLMHxc+5bt1gvAZfMv1LiO5agQ1szXWzbMpgTWLbszysw
EqXCv350GQrbK0YibFchUWdpprtpBX7KelUU9a2CZYSFwGrzKlBLmxOeJXAR
bd/6fDriy0XklBP6mMVcRPeVf9ptZLmJF1a6xdV9CMRjgyrpfhPcxN5ntp8O
7uIlfqbLvhiYJBDdLsWx7lPXEosUL/r7WvESPT8YtiR3CRKTayRcb7atIY5P
6eR57FtP/B8v3Fr4
"]]}, {}, {}}}, {}, {}, {{}, {}}},
AspectRatio->0.6180339887498948,
Axes->{False, False},
AxesLabel->{None, None},
AxesOrigin->{0, 0},
DisplayFunction->Identity,
Epilog->{{}, 
StyleBox[
LineBox[{{-8.557314213621972, -6.730706963341009}, {8.567038225661562,
         6.677415739228952}}], 
Directive[
RGBColor[0.368417, 0.506779, 0.709798], 
AbsoluteThickness[1.6], 
Dashing[{0, Small}]], StripOnInput -> False]},
Frame->{{True, True}, {True, True}},
FrameLabel->{{None, None}, {None, None}},
FrameStyle->Automatic,
FrameTicks->{{Automatic, Automatic}, {Automatic, Automatic}},
GridLines->{Automatic, Automatic},
GridLinesStyle->Directive[
GrayLevel[0.4, 0.5], 
AbsoluteThickness[1], 
AbsoluteDashing[{1, 2}]],
ImagePadding->All,
Method->{"CoordinatesToolOptions" -> {"DisplayFunction" -> ({
(Part[{{Identity, Identity}, {Identity, Identity}}, 1, 2][#]& )[
Part[#, 1]], 
(Part[{{Identity, Identity}, {Identity, Identity}}, 2, 2][#]& )[
Part[#, 2]]}& ), "CopiedValueFunction" -> ({
(Part[{{Identity, Identity}, {Identity, Identity}}, 1, 2][#]& )[
Part[#, 1]], 
(Part[{{Identity, Identity}, {Identity, Identity}}, 2, 2][#]& )[
Part[#, 2]]}& )}},
PlotLabel->FormBox["\"AAPL\"", TraditionalForm],
PlotRange->{{-2.852438071207324, 
     2.855679408553854}, {-3.5981403826688174`, 3.89671083743314}},
PlotRangeClipping->True,
PlotRangePadding->{{
Scaled[0.02], 
Scaled[0.02]}, {
Scaled[0.02], 
Scaled[0.02]}},
Ticks->{Automatic, Automatic}]\), \!\(\*
GraphicsBox[{{}, {{
{Hue[0.9060679774997897, 0.6, 0.6], Opacity[0], Dashing[Small], 
        LineBox[{{-8.282742573545612, -3.7696723729864274`}, \
{-3.7842085071390166`, -3.7696723729864274`}}]}, 
{Hue[0.9060679774997897, 0.6, 0.6], Opacity[0], Dashing[Small], 
        LineBox[{{3.0076215921420832`, 3.037337418556066}, {
         8.273634113938336, 3.037337418556066}}]}, {}, 
{Hue[0.9060679774997897, 0.6, 0.6], Opacity[0], 
        LineBox[{{-3.7842085071390166`, -3.7696723729864274`}, {
         3.0076215921420832`, 3.037337418556066}}]}}, {{}, 
{RGBColor[0.368417, 0.506779, 0.709798], PointSize[
        0.007333333333333334], AbsoluteThickness[1.6], 
        PointBox[CompressedData["
1:eJwtlHk0FIz3xifSIkWRhFJkfROvtyxJd1KWalCSaCNLG0XSQiVEKUVZk1RE
SqRkKeEOirIbM5ZsM5jB2Ga1hHz9zvndc+75nOc5595z/7nPRhcvW3cRAoEw
Nd//R2YQV/uo7CKybt/W2b0aK8h5EoY3EjJFyXlhipumSBLk2pTGGs4BEbIV
G0U7NBeR7TWehKx0WEDWmkn1MgleQE6esfbJiiaQT9fr0z8FLiBPpRyuItHn
EKw/89ZtJZA/n+Qa3Kn4i75Hkr0LdQnkXY8+OrFrZ7Hl68U/VjdnMXRPsWnZ
6Aw29Nta6yvP4M3/8jLLVGbwW0K0IDxvGt12TI6pnZvGHQ2JjMPz2vqyTK5q
0R80arX3k7k1hXV2wtmX8n9wV7vhgZVLp/BhH+HuaPAU0jpDRQO1J3GDe8k7
Mn8SD35aNGv3bQLTmq/LLvKcxA/WB0ZW2E9g4dvEnd3sCYz4+WSE2CHE7XJ9
u6K8JvDukocuC9uFKHXTihY8NY7rxSLboyyE+ICZa7I5bBxP7VjzXDFDgHLi
D0sVFcYxn8IS5j0SYG9GswbvkxBL8xvPmJEEeC/HSfQISYg5cU+PTt/iY7h4
fDCBLcCVOZnU2Jt89BmbK8t8IEDiMcvDbz34WOqwwGPjFgGmSty0adbj42Y5
argWlY/0nrCzDzg8zMzTzU+Yn4uQNwl5mMNDl2VMAzN1PrL2mdSOk3h4Y0Lc
fzGVh9tNTk/4ruBhjneAX0kwD+83LnwT9Y6LfrqJdvv/m/dt+1dlpXBxXPoY
+wmTi+TsM1r/eHExW6/k3vUELnafUI2w9OTiei+x5H5rLnqam8/47eVi8Ibv
Mb/EuBjXnrrsVC8Hw2HLNfESDuZU6re6NXHQJc+uL/4aB6kyCeSOLA56/TZp
ddbj4DG9gUcH4zhoSeesed8xhpsKPjpIOHGw0bQjq85+DE1+9VeqzPuD1Z/V
VzaNIvFUQKLP1Cjq6pJXOh4cxQig3TlOGcW4D3mpEY0jGBu8zsvvxDBqVc28
TDw0gmluauSTz4fQPmiFhkfLMDrOFR+39xrC1P6TbwePD2Nw08ULROkhtPVz
+7Kwbwhf6yzjni5iY1r5UdH3nkMoMNC5OPWVjbdSPPVqxtkYEBJ9PTR9EPOp
s60OwWx8HezVlVQ+gARXmoupJBs9hrsXaz0bwJlYnuiNpEE8n6Vy1ebyAP4g
dr4Tbh5EoSTv2zMmC7tULUfTigdwr3oCtYvGwhAXhnigzQCm+xr8Z01mYYHh
v3XXe/qRvU9D/bkKC+WcPZ6EXu3HLsO/7m2TTFSyldd5vqwfFbWPGBt9ZmIk
PeJPTjIL2yxiFz4NZuIqBuEL2ZCFKRVvH8hKMrGSYRNb1MBE6mF7w0RqH04U
26m8OMfEs+f7TgxR+pD8ON/mhCgTrU+4Esqie/H5uL4TL6kPz0zvufxYqRct
qecHDhv1oWb+26SKnB6sm6TVBdJ6cbApu+5cKQNpI847PX16kU+a2aAZz0Az
zY3pK6V6Mcnt3EgaiYH9CZ5fz3/owTCr7Q3HxRlYZKjncsmqB0XNV/+zY5iO
EcwnlUojDFTWT/E3vUjH884fzLwfMbA5P7Tghh0dv37I9TixhYGgNOLjuLAb
Xd7JTDHq6fiw82mK0/0u1KSxfk9eouO63YaqF3W6sGjuhmaSDB1V2nttH6zv
wrEWNVKMVzeOqZRpGq/twudw7tJ4fhdO/Hn90sK1c/7v7TqOzHViATFpdV5r
B9rmbRvOtuzEoMv3ZRmv5zUlwHQ8qgP1+BHXpL+343IjN1TumqfqvhbtiN/o
z8gK0NZqxyhymm/VwzbUDs+lrrj2G5elJLUdYreiqcr9/fi9DSUctifTO1vR
2WT3KwPpNpxNNZkoLmnFNPZlsrdLKxb5f897c7oVPS4WVrrmtGDeX1K6Oa0Z
44Ouzy4VbUG/2hmR1ms0VFmQSjlu14zNiwesDCOpqLQ8t/vwGxqWUybbusIb
UaEsvWd0kop/hHbZZGIj0lo3FW8kUZFYtbL6q14jfojL9Bl42YSJ8upq7l61
WB/LVDMRUNBbi5dQ/LcGw8WmFOT3UvBK+paQyMBKjFQQ+eT3ohFt0jM7IvZV
4OydCGd7QQO+X/vGhnr4B8bkbMGMfQ1oJhtFN676joGrtAQ9pvWIrCO9n4fL
0exz6Pt93FqUN9O90iBTjhszQxyDX9WgK6vfYltIGTpotXXcPlCNigcXtqcy
yKjw8Yqx0YIqxPyy6meyiPIv9rxKzfmJ1pJ3fkTeLMaHlnyHL26VSL+35tXG
TcXYZlTfdH5NBa52TbEvVPuGjCO5STnzd2TsU0+ySy7AkU/izncDyrHtb8nu
IrkCLK2hdHXoleFutfpX9yby8dcBHM/sJ6Oj53n/lCv5+GN1vn67EaJBsXuf
sVo+ivr7ZvyTVoQk/bmB3qxcjA/3DDRaWYjmnJdHbEo+4+NT7tL8WwVYf6Op
SkfhI7Y+oXWaD+Xi395TFnGG2dj28tFVFccclJntKc+I+YBXJejyYxHZ6F8T
Xrw8KhW/Xznf4OqZgXaMsy+jT6ei/GbfkuB9abgE/LXuNKdgwYYPuZqar/Ae
h36zST8G11tO61+QisOPCQW+To3RWJUhU7DuxT0k/H/1x3+xN+92wMLyg7d5
tBjYEHp6I+l0EKjaJU9E+MSD8rZNniGCKIglegmvKrwGny2hL87rJ8GYtXoM
7+FnCEtZ4hhR9Bqu+MuKvNv7BcyH/5736noLYrKVNkpzX6Ev2DfvD+ED5Bux
Cd0fCkGyvWW3ZtQnWPum1FLNoxjkapXekzblwuIL/f22j4qh4nk2fTI/H6Ty
mGbBs2Roqci3gn1fIQh12wudS0Enr+Tav13foLukzlt+UTlMHyAsZPiUwIXS
svrSgxVw7qJbp04IGQovKez/8rsCjrOv/XCqL4X1JIt/cowrIaw+23ypQjkE
hUXJXXauhKArjiHbznwHA+bkhQTXX+B7xLdw5PMP8HXy6LKQq4HNp5+C8YJK
qCRk2hXm18DHb4N31W1+QmzzWEGmWC3k18orFyX9guuUtLRgr1qYtAgoFxmp
gp+vfE69JtRB0S9NophJDQRJaOkMKDQAvUErqvZRLUj1/Oo5rNkAG3Trf7t3
1wEh0GZB/4MGcNkVpDcs1wA60SXXZyMboXYVoym+rAF+VSnfWz7WCEcz7DZ9
82wE2r6dpqbCRnCI2R95bA0FxhadPFNSTIGXmwyfBZRRwHNi74a3NRS4oTrH
1LzYBGtNA9P9minw+sw1XVd5KvRLJR3cxqLA0IE/h3UrqVD/grNqQkiBkcRF
h+J9afDE56uFrGQT8CPHzV4oN4Piuk6Kh1UTuEhVe+9vbAYrzZ3xzKQmMJqV
ME4LbIFQys40iYYmuOJX8V+ObiuIi7pjpSoVtGtipf0YrSAS+yNC6R0VJHPa
SwjRbRBbnm52by8NZtcutjxg9hvu/mr4eHNPM1h4E3gXJ3+DeP3m9hcOzdBZ
ma/nltkOO+vfVcjyWkDxVGOewakO0HvuOXVquhWU9oQ5cWU7YcPJjkvjzb8h
oPONTUJtJxj4i2o7H2+Hc3Xf+gxCu+AescnSt74Lik77Ic2kGzbJqSV53+4G
y/mQujHRDWt0axKOaNEhUvFxzFpHOpgFaI3nZdChilOcI1JAB87gDUL5Jzoo
jZ9QDVjNgKhPNZ3utgxoTD8y99iXAVyW/3+nfjBgfLNxEJHKgOWsKqGEWg+o
BLYrRG3tgVmFkd3mRj1AYqy+HB7bA6Z26aH19T2Q5V3lrDfRA2d8vWjJkz2w
Y5v45EPHXtgqvN6qPU994u2w5KJeEK9bLHHWvg+yFGRSrm7og+1+FSu4mkwQ
2UmXkw7tg13AZ4bGM0Gj1WlpALsPDFyKJRkKLDgh9rej5AAT7vqdsy3cyAId
zSnrzgImdD76HOR2hgX+GhmXGEos2FD2lp6QzQKhumFuUxgLSEtSHAorWHAv
oXygiMcCkzlWvW4PCwLSZfa/OdEPyheGzlU/64d1gb/vJfzqh9ZGjduxRgMw
/O7B91f6AzDhe+jZ+scDsPsCN70idQCqxKLfsVkDoB1211VWZhCKby1f5S0+
CG6dicWJIYNwVC0usf4yG05nBCi6jg9C1o77BGEIG9Yrpkf5nWNDKD89fbqV
Dd2Dq4eHO9kg3vCFZLxjCCSWLSyuPjQE2yk/RzZbDUEhebmPavUQBGUV3JZ3
HYKlOktcxPcMw+DobmsV7yEo+VnACC8ZhiyVtgX85CGIWvnGsWj7CGQuHItc
ljUEs8KTJ7O/jMC0cUDu5fYheHrtXLWf4SiQAqUtKGLDQJI+wfi3cBRQXyX3
jXAYDB+EnhkzGQPraX/ptkWj8FH9WWN1+Ri0s4qkqqVGQTlg1TauKgfyL52Z
PO8+CrKOmrs0PDiQp97nZv1+FKBXhPrsEwdEl1YlH+WOwtbvT7mOUxxoqXa/
QuCPAmXV79lrplxwmjMILVs7Bs7NUX1LHnFB5Cw8iTbmwLsCHQvlNi4MDujy
18dyQJvq9aldjQcOwd7yq2Y54CZzqNn6Kg9srboih5ZyQTuxuzm+kgd3/NVr
YyS5IJv9NYYmz4db4ZUj7ju5cNJRTFrLmz+f028OnN3Phe5vbwcKK/kQx+Dr
zY1x4dIMrfLTRgFs9/AaFpPngWo0VckkQAANBj+XLt/GA/jg0f24UwDRz5Ys
WPiaBwb2W537QQg/Qn0H3mrxIcb6fWhwmhA0nvSwCyf4UJPlvD5rxTg0rH0k
1U4SwI77958V3RiHwNdyVTsOC+C7krKe9Mg49D+4aZx0UgDD3768UHadgJS4
uuqwCwI4S/JO9OqagOLDcWzPOwJw9Le6HOc0CWfUgyUzqgXQuCR60cH+SdBr
/7jxlqIQdobRegKuTsG3IMrdWwNCCJ78dVR3xR94WiCI2GI5CYQ1g1L52X/A
XPOgV9b8ntX0GlLB8WmQbElK3C0/BVot95ceWjMD0QTF7yvCp2DrwJOXtj0z
oBMpXSidNAd83dAi/9JZKLX6k6eVPgfOIhUx0oV/YVHjzf1tygTiW3Mt9c6m
OTh7sdte3I1A9Lf++urKIwIRzzY6fPEiEP/xn85pO7iAOBoYMjSxV4SYKjCe
/rJPhHiR/1CJflqEGHwy5d2pN6LE4xrP/3oeW0z82HTsuLLUIqL58M3Ia6Ql
xP8BO4x5NA==
"]]}, {}, {}}}, {}, {}, {{}, {}}},
AspectRatio->0.6180339887498948,
Axes->{False, False},
AxesLabel->{None, None},
AxesOrigin->{0, 0},
DisplayFunction->Identity,
Epilog->{{}, 
StyleBox[
LineBox[{{-8.282742573545612, -8.278260631231932}, {8.273634113938336,
         8.315119441113826}}], 
Directive[
RGBColor[0.368417, 0.506779, 0.709798], 
AbsoluteThickness[1.6], 
Dashing[{0, Small}]], StripOnInput -> False]},
Frame->{{True, True}, {True, True}},
FrameLabel->{{None, None}, {None, None}},
FrameStyle->Automatic,
FrameTicks->{{Automatic, Automatic}, {Automatic, Automatic}},
GridLines->{Automatic, Automatic},
GridLinesStyle->Directive[
GrayLevel[0.4, 0.5], 
AbsoluteThickness[1], 
AbsoluteDashing[{1, 2}]],
ImagePadding->All,
Method->{"CoordinatesToolOptions" -> {"DisplayFunction" -> ({
(Part[{{Identity, Identity}, {Identity, Identity}}, 1, 2][#]& )[
Part[#, 1]], 
(Part[{{Identity, Identity}, {Identity, Identity}}, 2, 2][#]& )[
Part[#, 2]]}& ), "CopiedValueFunction" -> ({
(Part[{{Identity, Identity}, {Identity, Identity}}, 1, 2][#]& )[
Part[#, 1]], 
(Part[{{Identity, Identity}, {Identity, Identity}}, 2, 2][#]& )[
Part[#, 2]]}& )}},
PlotLabel->FormBox["\"INTC\"", TraditionalForm],
PlotRange->{{-2.7609141911818704`, 
     2.757878037979445}, {-3.7696723729864274`, 3.037337418556066}},
PlotRangeClipping->True,
PlotRangePadding->{{
Scaled[0.02], 
Scaled[0.02]}, {
Scaled[0.02], 
Scaled[0.02]}},
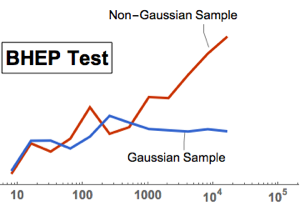
Ticks->{Automatic, Automatic}]\)}

Realize um teste de normalidade multivariado com BaringhausHenzeTest (BHEP). A suposição de normalidade é claramente rejeitada.

In[6]:=

htd = BaringhausHenzeTest[fdata, "HypothesisTestData"];

In[7]:=

htd["TestDataTable"]

In[8]:=

\!\(\*
StyleBox[
TagBox[GridBox[{
{"\<\"\"\>", "\<\"Statistic\"\>", "\<\"P\[Hyphen]Value\"\>"},
{"\<\"Baringhaus\[Hyphen]Henze\"\>", "3.69066", "0.`"}
},
AutoDelete->False,
GridBoxAlignment->{
    "Columns" -> {{Left}}, "ColumnsIndexed" -> {}, 
     "Rows" -> {{Automatic}}, "RowsIndexed" -> {}, "Items" -> {}, 
     "ItemsIndexed" -> {}},
GridBoxDividers->{
    "Columns" -> {}, "ColumnsIndexed" -> {2 -> GrayLevel[0.7]}, 
     "Rows" -> {}, "RowsIndexed" -> {2 -> GrayLevel[0.7]}, 
     "Items" -> {}, "ItemsIndexed" -> {}},
GridBoxItemSize->{
    "Columns" -> {{Automatic}}, "ColumnsIndexed" -> {}, 
     "Rows" -> {{Automatic}}, "RowsIndexed" -> {}, "Items" -> {}, 
     "ItemsIndexed" -> {}},
GridBoxSpacings->{
    "Columns" -> {{Automatic}}, "ColumnsIndexed" -> {}, 
     "Rows" -> {{Automatic}}, "RowsIndexed" -> {}, "Items" -> {}, 
     "ItemsIndexed" -> {}}],
"Grid"], "DialogStyle",
StripOnInput->False,
"NodeID" -> 379]\)

In[9]:=

htd["ShortTestConclusion"]

Out[9]=

Ajuste os dados filtrados com MultinormalDistribution e MultivariateTDistribution.

In[10]:=

multiN = EstimatedDistribution[fdata, 
  MultinormalDistribution[Array[x, 5], Array[s, {5, 5}]]]

Out[10]=

In[11]:=

multiT = EstimatedDistribution[fdata, 
  MultivariateTDistribution[Array[x, 5], Array[s, {5, 5}], nu]]

Out[11]=

Calcule o AIC para duas distribuições. O modelo de MultivariateTDistribution possui um valor menor.

In[12]:=

aic[k_, dist_, data_] := 2 k - 2 LogLikelihood[dist, data]

In[13]:=

aic[5 + 15, multiN, fdata]

In[14]:=

3273.13

In[15]:=

aic[5 + 15 + 1, multiT, fdata]

In[16]:=

2931.76

Exemplos Relacionados

Cobertura de distribuição expandida

Computação mais rápida de propriedades de distribuição

Estimativa de distribuição mais rápida

Modelagem de redes sociais

Mais simplificação automática para distribuições transformadas

Função densidade de probabilidade para produto/quociente de variáveis aleatórias

Melhoria da amostragem de distribuições truncadas

Segmentação de imagem com um modelo mistura gaussiano

Normalização de distribuições de fórmula

Manipule descontinuidades em uma função distribuição acumulada

Faça uma amostragem de uma densidade de polinômios

Amostragem aleatória de uma determinada função densidade de probabilidade

Amostragem de pontos em regiões

Crie uma amostra de um processo de pontos de Poisson

Processo de Poisson não homogêneo

Estimativa de processos aleatórios com amostras irregulares

Melhor desempenho de binning de dados

Teste de normalidade multivariado

Retornos logarítmicos de preços de ações

Análise de dados de doenças cardíacas