ポアソン点過程からのサンプル
ポアソン(Poisson)点過程は,一次元ポアソン過程を多次元ポアソン過程に一般化したものである.幾何領域における同次ポアソン点過程は,RandomPointを使ってサンプリングすることができる.
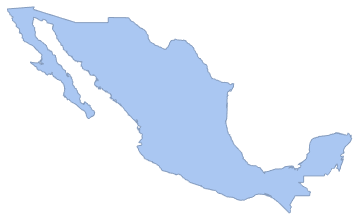
国の多角形を作成する.
In[1]:=
region = DiscretizeGraphics[CountryData["Mexico", "Polygon"],
ImageSize -> Medium]Out[1]=
領域,強度,実現数という3つの引数でポアソン点過程のサンプルを取る関数を定義する.
In[2]:=

ppp[region_, intensity_, n_] := Module[{nlist, pts},
nlist =
RandomVariate[PoissonDistribution[intensity RegionMeasure[region]],
n];
pts = RandomPoint[region, Total[nlist]];
nlist = Accumulate[nlist];
nlist = Transpose[{Prepend[Most[nlist] + 1, 1], nlist}];
Table[Take[pts, ind], {ind, nlist}]
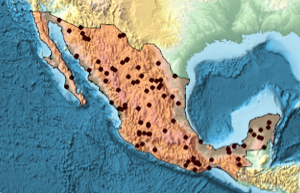
]国の多角形で強度0.5のポアソン点過程の実現を生成し,これをGraphicsを使って可視化する.
In[3]:=
intensity = 0.5;
sample = ppp[region, intensity, 1];In[4]:=
Show[region, Graphics[{Black, Point @@ sample}]]Out[4]=
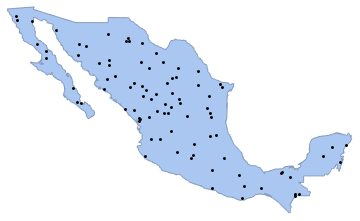
同じ過程から104個のサンプルを生成する.各サンプルの点の総数は,平均が強度に領域の面積を掛けたものに等しいPoissonDistributionを満足する.
In[5]:=
samples = ppp[region, intensity, 10^4];
counts = Length /@ samples;In[6]:=

htd = PearsonChiSquareTest[counts,
PoissonDistribution[intensity RegionMeasure[region]],
"HypothesisTestData"];In[7]:=
htd["TestDataTable"]Out[7]=
In[8]:=
htd["TestConclusion"]Out[8]=
任意の部分領域における点の数もポアソン分布に従う.ここでは,多角形内にある円板について,円板の中の点の数を数えてこれを確かめる.
In[9]:=
disk1 = Disk[{-107, 28}, 1.5];
Show[region, Graphics[{Red, disk1}]]Out[9]=
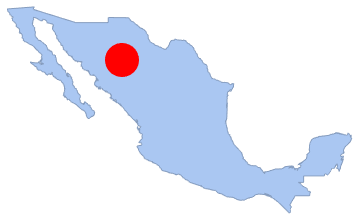
In[10]:=
memberfun1 = RegionMember[disk1];
counts1 = Table[Total[Boole[memberfun1[pts]]], {pts, samples}];PearsonChiSquareTestをポアソン分布の点の数について行う.
In[11]:=

htd = PearsonChiSquareTest[counts1,
PoissonDistribution[intensity RegionMeasure[disk1]],
"HypothesisTestData"];In[12]:=
htd["TestDataTable"]Out[12]=
In[13]:=
htd["TestConclusion"]Out[13]=
離れたところにある任意の部分領域における点の数は独立している.ここでは,2つの重なり合わない円板内の点の数を数え,SpearmanRankTestを行う.
In[14]:=
disk2 = Disk[{-100, 20}, 1.3];
Show[region, Graphics[{Red, disk1, Blue, disk2}]]Out[14]=
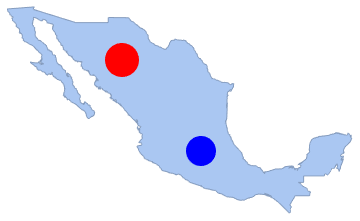
In[15]:=
memberfun2 = RegionMember[disk2];
counts2 = Table[Total[Boole[memberfun2[pts]]], {pts, samples}];In[16]:=
htd = SpearmanRankTest[counts1, counts2, "HypothesisTestData"];In[17]:=
htd["TestDataTable"]Out[17]=
In[18]:=
htd["TestConclusion"]Out[18]=