Wolfram Language™

Crie uma amostra de um processo de pontos de Poisson

Um processo de pontos de Poisson é uma generalização do processo de Poisson unidimensional para um caso multidimensional. Um processo homogêneo de Poisson em regiões geométricas podem ser amostrados usando RandomPoint.

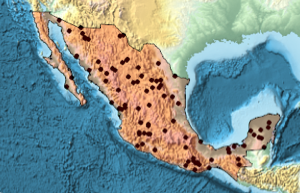
Crie um polígono de país.

In[1]:=

region = DiscretizeGraphics[CountryData["Mexico", "Polygon"], ImageSize -> Medium]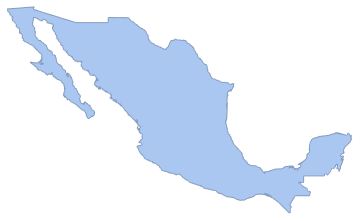

Out[1]=

Defina uma função que faça uma amostra de um processo de pontos de Poisson com três argumentos: região, intensidade, e número de realizações.

In[2]:=

ppp[region_, intensity_, n_] := Module[{nlist, pts}, nlist = RandomVariate[PoissonDistribution[intensity RegionMeasure[region]], n]; pts = RandomPoint[region, Total[nlist]]; nlist = Accumulate[nlist]; nlist = Transpose[{Prepend[Most[nlist] + 1, 1], nlist}]; Table[Take[pts, ind], {ind, nlist}] ]

Gere uma realização do processo de Poisson no polígono de país com intensidade de 0,5 e visualize com Graphics.

In[3]:=

intensity = 0.5; sample = ppp[region, intensity, 1];

In[4]:=

Show[region, Graphics[{Black, Point @@ sample}]]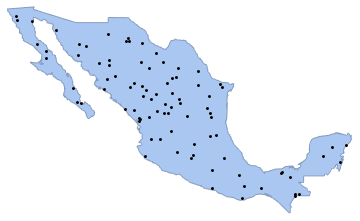

Out[4]=

Gere 10⁴ amostras do mesmo processo. O número total de pontos em cada amostra satisfaz PoissonDistribution, com a média igual a intensidade vezes a área da região.

In[5]:=

samples = ppp[region, intensity, 10^4]; counts = Length /@ samples;

In[6]:=

htd = PearsonChiSquareTest[counts, PoissonDistribution[intensity RegionMeasure[region]], "HypothesisTestData"];

In[7]:=

htd["TestDataTable"]

Out[7]=

In[8]:=

htd["TestConclusion"]

Out[8]=

O número de pontos em qualquer sub-região também é uma distribuição de Poisson. Aqui, é examinado com um disco que se encontra dentro do polígono, e o número de pontos nele é contado.

In[9]:=

disk1 = Disk[{-107, 28}, 1.5]; Show[region, Graphics[{Red, disk1}]]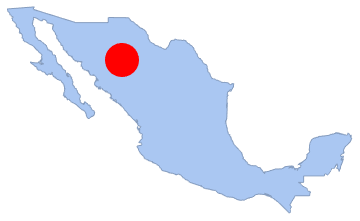

Out[9]=

In[10]:=

memberfun1 = RegionMember[disk1]; counts1 = Table[Total[Boole[memberfun1[pts]]], {pts, samples}];

Faça um PearsonChiSquareTest no número de contagens, com uma distribuição de Poisson.

In[11]:=

htd = PearsonChiSquareTest[counts1, PoissonDistribution[intensity RegionMeasure[disk1]], "HypothesisTestData"];

In[12]:=

htd["TestDataTable"]

Out[12]=

In[13]:=

htd["TestConclusion"]

Out[13]=

O número de pontos em quaisquer sub-regiões disjuntas é independente. Aqui, o número de pontos em dois discos disjuntos é contado, e um teste SpearmanRankTest é realizado.

In[14]:=

disk2 = Disk[{-100, 20}, 1.3]; Show[region, Graphics[{Red, disk1, Blue, disk2}]]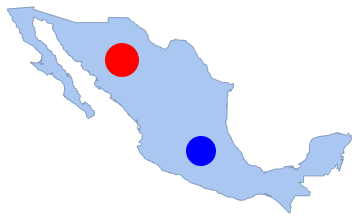

Out[14]=

In[15]:=

memberfun2 = RegionMember[disk2]; counts2 = Table[Total[Boole[memberfun2[pts]]], {pts, samples}];

In[16]:=

htd = SpearmanRankTest[counts1, counts2, "HypothesisTestData"];

In[17]:=

htd["TestDataTable"]

Out[17]=

In[18]:=

htd["TestConclusion"]

Out[18]=