Stichproben aus einem Poisson-Punktprozess

Ein Poisson-Punktprozess ist eine multidimensionale Verallgemeinerung des eindimensionalen Poisson-Prozesses. Ein homogener Poisson-Punktprozess in geometrischen Regionen kann mittels RandomPoint erzeugt werden.

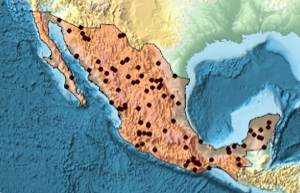
Erstellen Sie das Polygon eines Landes.

In[1]:=

region = DiscretizeGraphics[CountryData["Mexico", "Polygon"], ImageSize -> Medium]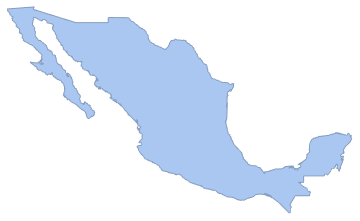

Out[1]=

Bestimmen Sie eine Funktion zur Stichprobennahme des Poisson-Punktprozesses mit drei Argumenten: Region, Intensität und Anzahl der Realisierungen.

In[2]:=

ppp[region_, intensity_, n_] := Module[{nlist, pts}, nlist = RandomVariate[PoissonDistribution[intensity RegionMeasure[region]], n]; pts = RandomPoint[region, Total[nlist]]; nlist = Accumulate[nlist]; nlist = Transpose[{Prepend[Most[nlist] + 1, 1], nlist}]; Table[Take[pts, ind], {ind, nlist}] ]

Generieren Sie eine Realisierung des Poisson-Punkprozesses im Länder-Polygon mit Intensität 0,5 und visualisieren Sie ihn mit Graphics.

In[3]:=

intensity = 0.5; sample = ppp[region, intensity, 1];

In[4]:=

Show[region, Graphics[{Black, Point @@ sample}]]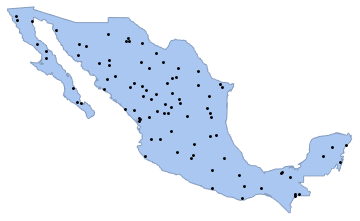

Out[4]=

Generieren Sie 10⁴ Stichproben desselben Prozesses. Die Gesamtzahl der Punkte in jeder Stichprobe erfüllt die PoissonDistribution, wobei der Mittelwert gleich zur Intensität Mal Flächeninhalt der Region ist.

In[5]:=

samples = ppp[region, intensity, 10^4]; counts = Length /@ samples;

In[6]:=

htd = PearsonChiSquareTest[counts, PoissonDistribution[intensity RegionMeasure[region]], "HypothesisTestData"];

In[7]:=

htd["TestDataTable"]

Out[7]=

In[8]:=

htd["TestConclusion"]

Out[8]=

Generieren Sie 10⁴ Stichproben desselben Prozesses. Die Gesamtzahl der Punkte in jeder Stichprobe erfüllt die PoissonDistribution, wobei der Mittelwert gleich zur Intensität Mal Flächeninhalt der Region ist.

In[9]:=

disk1 = Disk[{-107, 28}, 1.5]; Show[region, Graphics[{Red, disk1}]]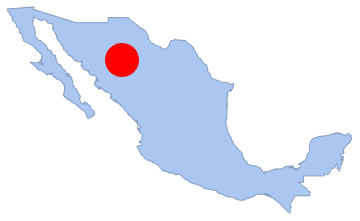

Out[9]=

In[10]:=

memberfun1 = RegionMember[disk1]; counts1 = Table[Total[Boole[memberfun1[pts]]], {pts, samples}];

Prüfen Sie mit dem PearsonChiSquareTest die Anzahl der Zählungen mit einer Poisson-Verteilung.

In[11]:=

htd = PearsonChiSquareTest[counts1, PoissonDistribution[intensity RegionMeasure[disk1]], "HypothesisTestData"];

In[12]:=

htd["TestDataTable"]

Out[12]=

In[13]:=

htd["TestConclusion"]

Out[13]=

Die Zahl der Punkte in jeder beliebigen disjunkten Unterregion ist unabhängig. In diesem Beispiel wird die Anzahl der Punkte in zwei disjunkten Scheiben gezählt und der SpearmanRankTest durchgeführt.

In[14]:=

disk2 = Disk[{-100, 20}, 1.3]; Show[region, Graphics[{Red, disk1, Blue, disk2}]]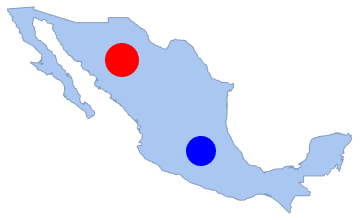

Out[14]=

In[15]:=

memberfun2 = RegionMember[disk2]; counts2 = Table[Total[Boole[memberfun2[pts]]], {pts, samples}];

In[16]:=

htd = SpearmanRankTest[counts1, counts2, "HypothesisTestData"];

In[17]:=

htd["TestDataTable"]

Out[17]=

In[18]:=

htd["TestConclusion"]

Out[18]=