Выборка из точечного процесса Пуассона

Точечный процесс Пуассона является обобщением одномерного процесса Пуассона и применяется для многомерных случаев. Однородный точечный процесс Пуассона в геометрической области может быть рассмотрен с помощью функции RandomPoint.

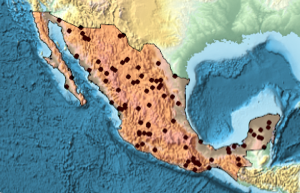
Создадим полигон для географического объекта, например, страны.

In[1]:=

region = DiscretizeGraphics[CountryData["Mexico", "Polygon"], ImageSize -> Medium]

Out[1]=

Определим функцию, которая делает выборку точечного процесса Пуассона с тремя аргументами: регион, интенсивность и количество реализаций.

In[2]:=

ppp[region_, intensity_, n_] := Module[{nlist, pts}, nlist = RandomVariate[PoissonDistribution[intensity RegionMeasure[region]], n]; pts = RandomPoint[region, Total[nlist]]; nlist = Accumulate[nlist]; nlist = Transpose[{Prepend[Most[nlist] + 1, 1], nlist}]; Table[Take[pts, ind], {ind, nlist}] ]

Сформируем реализацию точечного процесса Пуассона в данном полигоне с интенсивностью 0,5 и визуализируем результат с помощью функции Graphics.

In[3]:=

intensity = 0.5; sample = ppp[region, intensity, 1];

In[4]:=

Show[region, Graphics[{Black, Point @@ sample}]]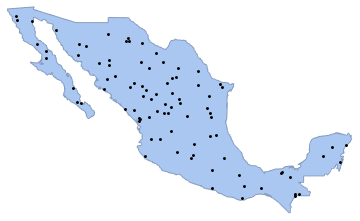

Out[4]=

Сформируем 10^4 образцов на основе того же процесса. Общее количество точек в каждом образце/выборкe соответствует распределению Пуассона (см. PoissonDistribution) со средним значением, равным произведению плотности и площади полигона.

In[5]:=

samples = ppp[region, intensity, 10^4]; counts = Length /@ samples;

In[6]:=

htd = PearsonChiSquareTest[counts, PoissonDistribution[intensity RegionMeasure[region]], "HypothesisTestData"];

In[7]:=

htd["TestDataTable"]

Out[7]=

In[8]:=

htd["TestConclusion"]

Out[8]=

Выборка точек в любом субрегионе полигона также распределена по принципу Пуассона. На рисунке ниже это проиллюстрировано с помощью красного круга, лежащего внутри полигона; посчитаем количество точек в данном субрегионе:

In[9]:=

disk1 = Disk[{-107, 28}, 1.5]; Show[region, Graphics[{Red, disk1}]]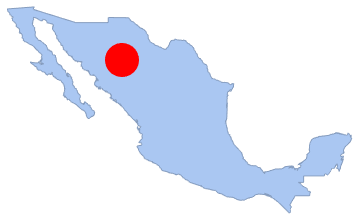

Out[9]=

In[10]:=

memberfun1 = RegionMember[disk1]; counts1 = Table[Total[Boole[memberfun1[pts]]], {pts, samples}];

Выполним тест хи-квадрат Пирсона с помощью функции PearsonChiSquareTest с количеством посчитанных точек в распределении Пуассона.

In[11]:=

htd = PearsonChiSquareTest[counts1, PoissonDistribution[intensity RegionMeasure[disk1]], "HypothesisTestData"];

In[12]:=

htd["TestDataTable"]

Out[12]=

In[13]:=

htd["TestConclusion"]

Out[13]=

Число точек в любых непересекающихся субрегионах не зависит друг от друга. В следующем примере рассчитаем число точек в двух непересекающихся субрегионах, закрашенных синим и красным цветом, и вычислим коэффициент корреляции Спирмана с помощью функции SpearmanRankTest.

In[14]:=

disk2 = Disk[{-100, 20}, 1.3]; Show[region, Graphics[{Red, disk1, Blue, disk2}]]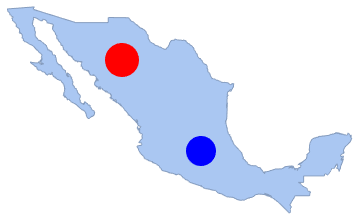

Out[14]=

In[15]:=

memberfun2 = RegionMember[disk2]; counts2 = Table[Total[Boole[memberfun2[pts]]], {pts, samples}];

In[16]:=

htd = SpearmanRankTest[counts1, counts2, "HypothesisTestData"];

In[17]:=

htd["TestDataTable"]

Out[17]=

In[18]:=

htd["TestConclusion"]

Out[18]=