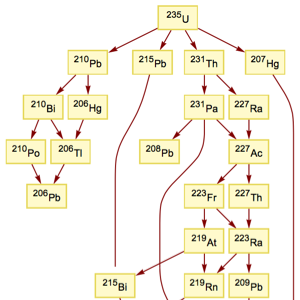
Encontre componentes conectados de grafos

Modele a rede de salto de um sapo a partir da densidade folha de uma vitória régia. A versão 11 inclui as funções ConnectedGraphComponents e WeaklyConnectedGraphComponents para análise de conectividade de redes.

Um sapo em uma lagoa de votória régia é capaz de saltar 1,5 pés para ir de uma das 25 folhas para outra.

In[1]:=

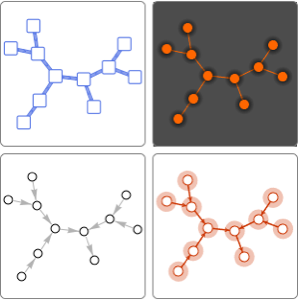
lilyDensity = MixtureDistribution[{1, 1, 1}, {BinormalDistribution[{0, 0}, {1, 1}, 0], BinormalDistribution[{-1, 4}, {1, 1}, -1/2], BinormalDistribution[{4, 4}, {1, 1}, 1/3]}]; lilyPond = SpatialGraphDistribution[25, 1.5, lilyDensity];

Pegue uma lagoa aleatória.

In[2]:=

g = RandomGraph[lilyPond, VertexShape -> \!\(\* GraphicsBox[ {EdgeForm[{Hue[0.3277777777777778, 0.16216216216216217`, 1.], Opacity[ 1.], AbsoluteThickness[1], CapForm["Round"]}], FaceForm[Hue[ 0.2388888888888889, 1., 0.9224857536122444]], PolygonBox[CompressedData[" 1:eJxTTMoPSmViYGCQAmIQDQYVhQ5gWiALQkeUQmiDPAj9ohxCcxRB6IwKCF1R DKF3QOVnlKDqvwGlT0DNzyiD0AE5ENoCyr+QBOVD9StEoupz8IHqy4XQDeZQ fiqEZtCG0AvioXxdVHMabKD8YKh5flDaG0I/iIbynaDuSYbqs4bQH2D2WkLo Dqg7HXwh9A+o/xdEQOgZVVD3Qc2xqIbQE9Kh/oLKf4CFNzQ8N0DDBRZ+BTkO ABBsOr4= "]]}, ImageSize->{45., Automatic}]\), VertexSize -> {"Scaled", 0.1}, EdgeStyle -> Opacity[0], Background -> Hue[0.6, 0.8, 0.4], ImageSize -> 150]

Out[2]=

Encontre a maior coleção de folhas de vitórias-régias sobre as quais o sapo pode saltar.

In[3]:=

VertexCount[First[ConnectedGraphComponents[g]]]

Out[3]=

Encontre o número de vezes que o sapo teria que nadar para visitar todas as vitórias régias.

In[4]:=

Length[ConnectedGraphComponents[g]] - 1

Out[4]=