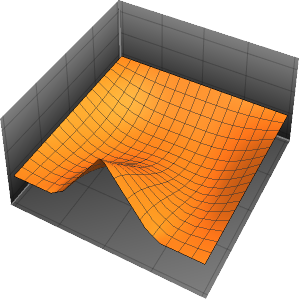
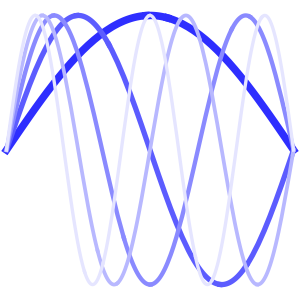
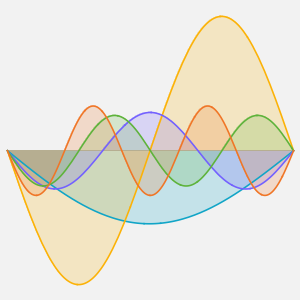
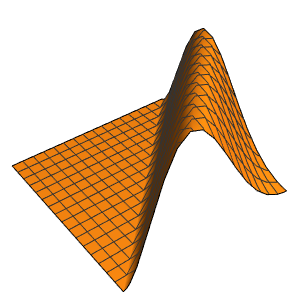
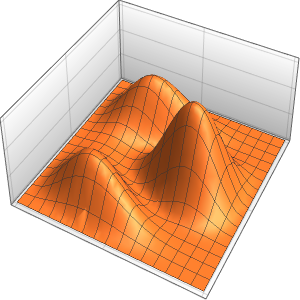
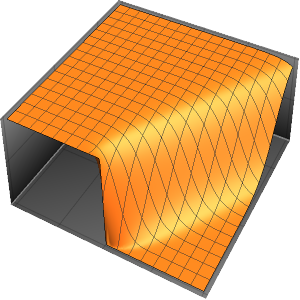
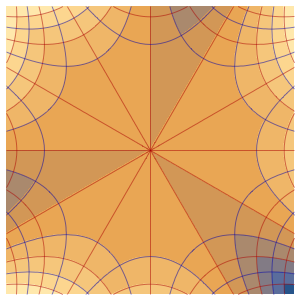
求解在立方体内带有周期性边界条件的泊松方程: Wolfram语言 11 的新功能

求解在立方体内带有周期性边界条件的泊松方程

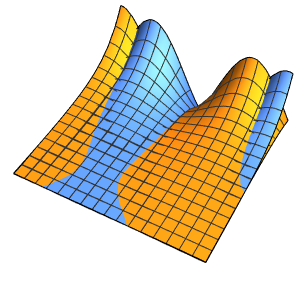
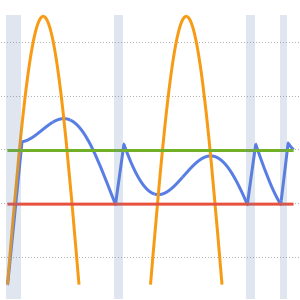
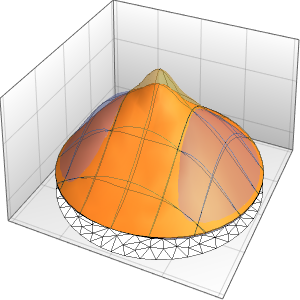
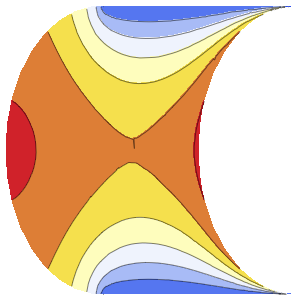
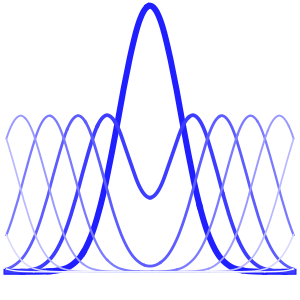
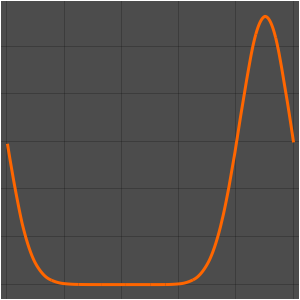
求解在立方体内带有周期性边界条件的泊松方程，其中右边区域的方程解投影到左边.

In[1]:=

\[CapitalOmega] = Cuboid[{0, 0, 0}, {5, 1, 1}];
ufun = NDSolveValue[{-Laplacian[u[x, y, z], {x, y, z}] == 1, 
   DirichletCondition[u[x, y, z] == 0, 0 < x < 5], 
   PeriodicBoundaryCondition[u[x, y, z], x == 0, 
    TranslationTransform[{5, 0, 0}]]}, 
  u, {x, y, z} \[Element] \[CapitalOmega]]

Out[1]=

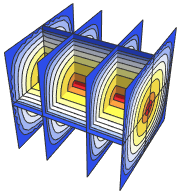
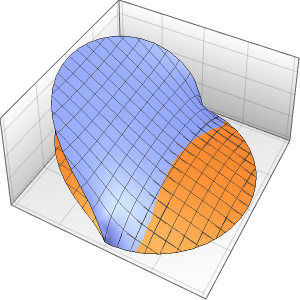
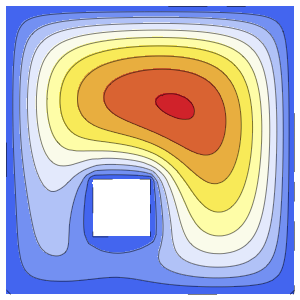
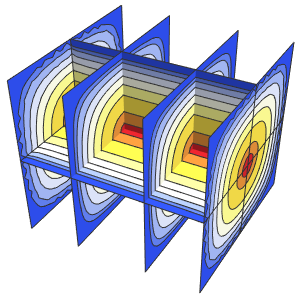
可视化方程的解.

In[2]:=

SliceContourPlot3D[
 ufun[x, y, 
  z], {{"XStackedPlanes", {0, 1.5, 3.5, 5}}, {"YStackedPlanes", 
   1}, {"ZStackedPlanes", 1}}, {x, y, z} \[Element] \[CapitalOmega], 
 ColorFunction -> "TemperatureMap", Boxed -> False, Axes -> False]

Out[2]=