Résolvez une équation de Poisson dans un cuboïde avec des conditions aux limites périodiques
Résolvez une équation de Poisson dans un parallélépipède avec des conditions aux limites périodiques où la solution du côté droit de la région est projetée sur le côté gauche.
In[1]:=

\[CapitalOmega] = Cuboid[{0, 0, 0}, {5, 1, 1}];
ufun = NDSolveValue[{-Laplacian[u[x, y, z], {x, y, z}] == 1,
DirichletCondition[u[x, y, z] == 0, 0 < x < 5],
PeriodicBoundaryCondition[u[x, y, z], x == 0,
TranslationTransform[{5, 0, 0}]]},
u, {x, y, z} \[Element] \[CapitalOmega]]Out[1]=
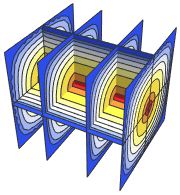
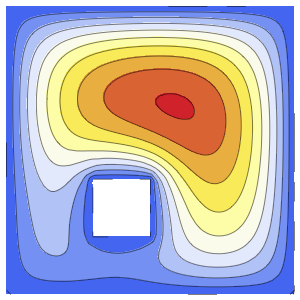
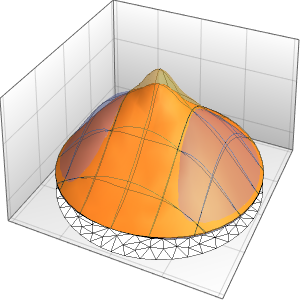
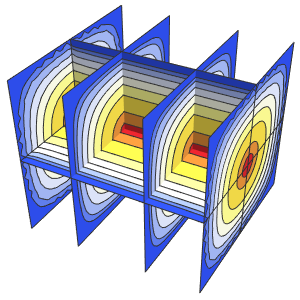
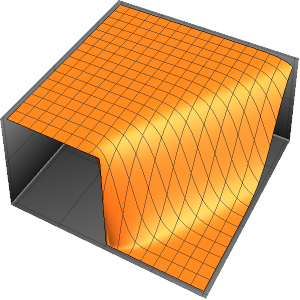
Visualisez la solution.
In[2]:=
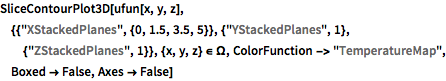
SliceContourPlot3D[
ufun[x, y,
z], {{"XStackedPlanes", {0, 1.5, 3.5, 5}}, {"YStackedPlanes",
1}, {"ZStackedPlanes", 1}}, {x, y, z} \[Element] \[CapitalOmega],
ColorFunction -> "TemperatureMap", Boxed -> False, Axes -> False]Out[2]=