事象についての偏微分方程式を領域上で解く: Wolfram言語 11の新機能

事象についての偏微分方程式を領域上で解く

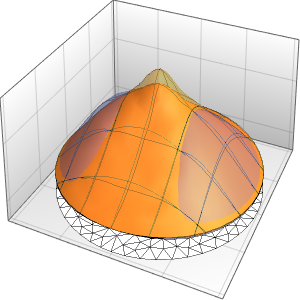
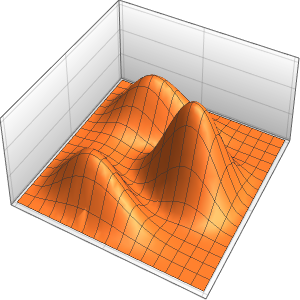
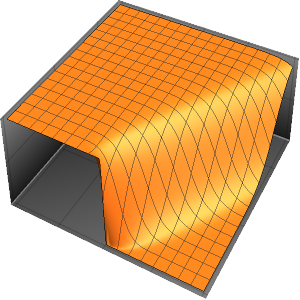
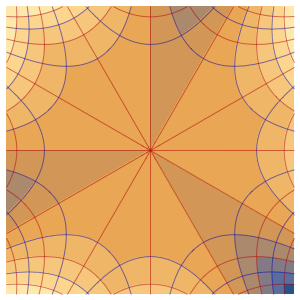
三方の壁が断熱壁で，一方の壁に外気温の影響を受けるガラスの窓がある部屋における，サーモスタットで制御された発熱をモデル化する．

In[1]:=

\[CapitalOmega] = Rectangle[{0, 0}, {3/2, 1}];
outsideTemp[t_] := 15 + 10*Sin[2 \[Pi] t/24];
kd = 0.78; Ld = 0.05;
\[CapitalGamma] = 
  NeumannValue[Ld/kd*(outsideTemp[t] - u[t, x, y]), {x == 0}];

暖房機の負荷は事象によって増加したり減少したりする．

In[2]:=

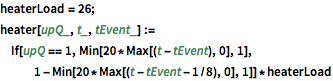
heaterLoad = 26;
heater[upQ_, t_, tEvent_] := 
 If[upQ == 1, Min[20*Max[(t - tEvent), 0], 1], 
   1 - Min[20*Max[(t - tEvent - 1/8), 0], 1]]*heaterLoad

偏微分方程式は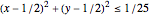，のサイクル内で熱を生成し，ガラスの窓から熱を失いながら，空気を通した熱拡散をモデル化する．

In[3]:=

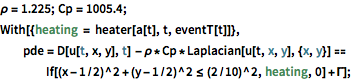
\[Rho] = 1.225; Cp = 1005.4;
With[{heating = heater[a[t], t, eventT[t]]},
  pde = D[u[t, x, y], t] - \[Rho]*Cp*Laplacian[u[t, x, y], {x, y}] == 
    If[(x - 1/2)^2 + (y - 1/2)^2 <= (2/10)^2, heating, 
      0] + \[CapitalGamma]];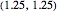

の位置にあるサーモスタットがトリガー信号より低い（または高い）温度を測定した場合，および離散変数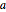が変化した場合に，暖房機はオン（またはオフ）になる．

In[4]:=

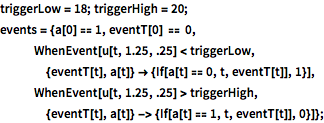
triggerLow = 18; triggerHigh = 20;
events = {a[0] == 1, eventT[0] == 0, 
   WhenEvent[
    u[t, 1.25, .25] < 
     triggerLow, {eventT[t], a[t]} -> {If[a[t] == 0, t, eventT[t]], 
      1}], WhenEvent[
    u[t, 1.25, .25] > 
     triggerHigh, {eventT[t], a[t]} -> {If[a[t] == 1, t, eventT[t]], 
      0}]};

外気温に等しい初期条件で偏微分方程式の時間積分を観察する．

In[5]:=

eqn = {pde, u[0, x, y] == outsideTemp[0], events};
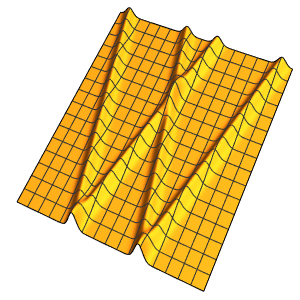
res = Monitor[
  NDSolveValue[
   eqn, {u, a}, {t, 0, 2*24}, {x, y} \[Element] \[CapitalOmega], 
   DiscreteVariables -> {eventT[t], a[t]}, 
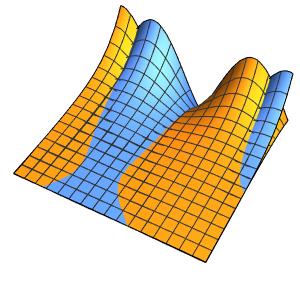
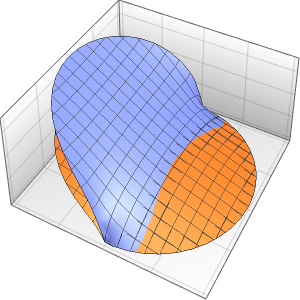
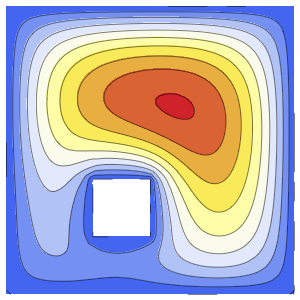
   EvaluationMonitor :> (monitor = Row[{"t = ", CForm[t]}])], monitor]

Out[5]=

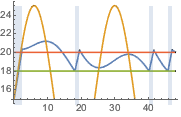
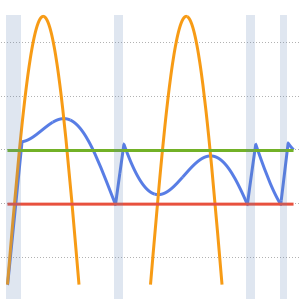
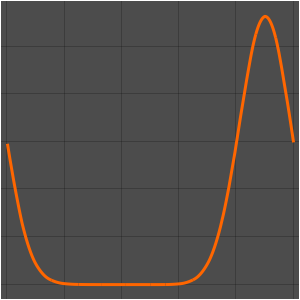
サーモスタットで測定された温度，外気温，暖房機のトリガー信号を可視化する．暖房機がオンになっている部分は青い背景色で示されている．

In[6]:=

hp = Plot[ 25 res[[2]][t], {t, 0, 2*24}, Filling -> Bottom, 
  PlotStyle -> None]; Show[
 Plot[{res[[1]][t, 1.25, .25], outsideTemp[t], 18, 20}, {t, 0, 
   2*24}], hp]

Out[6]=