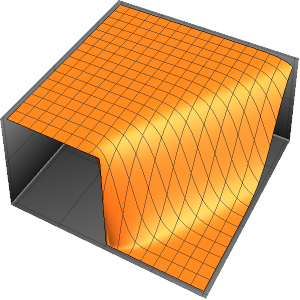
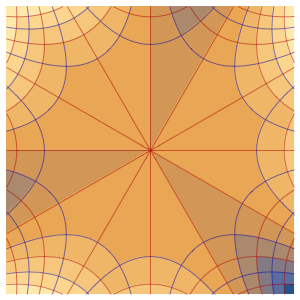
Résolvez des équations aux dérivées partielles avec des événements sur les régions : Nouveautés de Wolfram Language 11

Résolvez des équations aux dérivées partielles avec des événements sur les régions

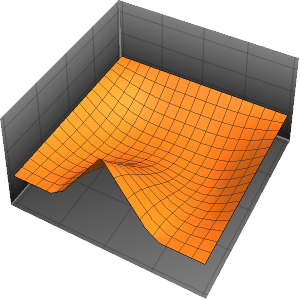
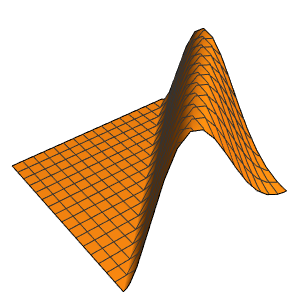
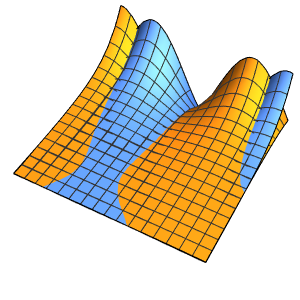
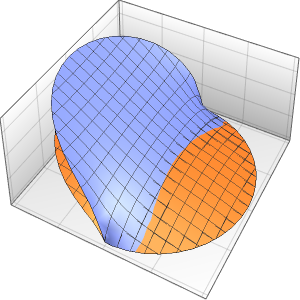
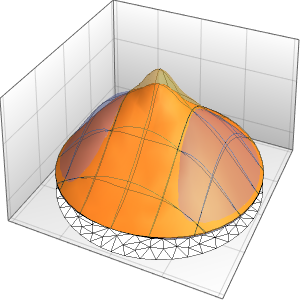
Modélisez la production de chaleur contrôlée par un thermostat dans une pièce avec trois murs isolés et une façade en verre soumise à la température extérieure.

In[1]:=

\[CapitalOmega] = Rectangle[{0, 0}, {3/2, 1}];
outsideTemp[t_] := 15 + 10*Sin[2 \[Pi] t/24];
kd = 0.78; Ld = 0.05;
\[CapitalGamma] = 
  NeumannValue[Ld/kd*(outsideTemp[t] - u[t, x, y]), {x == 0}];

La charge d'un appareil de chauffage est augmentée ou réduite lors d'un événement.

In[2]:=

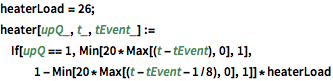
heaterLoad = 26;
heater[upQ_, t_, tEvent_] := 
 If[upQ == 1, Min[20*Max[(t - tEvent), 0], 1], 
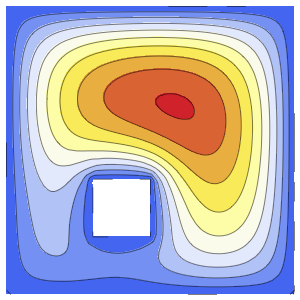
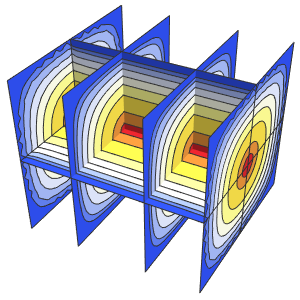
   1 - Min[20*Max[(t - tEvent - 1/8), 0], 1]]*heaterLoad

L'EDP modélise la diffusion de la chaleur dans l'air tout en générant de la chaleur à l'intérieur d'un cercle 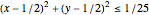et en perdant de la chaleur à travers la vitre.

In[3]:=

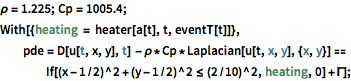
\[Rho] = 1.225; Cp = 1005.4;
With[{heating = heater[a[t], t, eventT[t]]},
  pde = D[u[t, x, y], t] - \[Rho]*Cp*Laplacian[u[t, x, y], {x, y}] == 
    If[(x - 1/2)^2 + (y - 1/2)^2 <= (2/10)^2, heating, 
      0] + \[CapitalGamma]];

Si le thermostat à la position 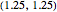mesure une température inférieure/supérieure à un seuil, et si la variable discrète 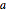a changé, le chauffage est activé/désactivé.

In[4]:=

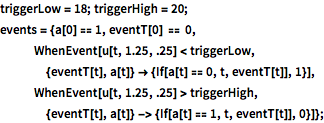
triggerLow = 18; triggerHigh = 20;
events = {a[0] == 1, eventT[0] == 0, 
   WhenEvent[
    u[t, 1.25, .25] < 
     triggerLow, {eventT[t], a[t]} -> {If[a[t] == 0, t, eventT[t]], 
      1}], WhenEvent[
    u[t, 1.25, .25] > 
     triggerHigh, {eventT[t], a[t]} -> {If[a[t] == 1, t, eventT[t]], 
      0}]};

Surveillez l'intégration temporelle de l'équation aux dérivées partielles avec la condition initiale égale à la température extérieure.

In[5]:=

eqn = {pde, u[0, x, y] == outsideTemp[0], events};
res = Monitor[
  NDSolveValue[
   eqn, {u, a}, {t, 0, 2*24}, {x, y} \[Element] \[CapitalOmega], 
   DiscreteVariables -> {eventT[t], a[t]}, 
   EvaluationMonitor :> (monitor = Row[{"t = ", CForm[t]}])], monitor]

Out[5]=

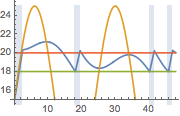
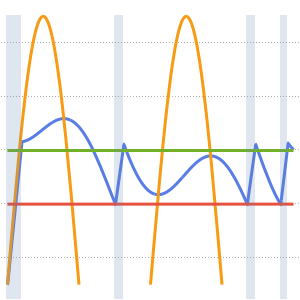
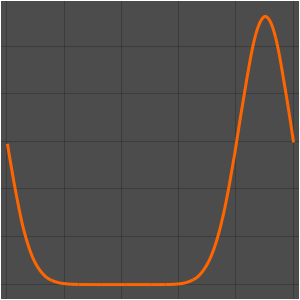
Visualisez la température mesurée au niveau du thermostat, la température extérieure et les éléments déclencheurs de l'appareil de chauffage. Un fond bleu est représenté là où le chauffage est en marche.

In[6]:=

hp = Plot[ 25 res[[2]][t], {t, 0, 2*24}, Filling -> Bottom, 
  PlotStyle -> None]; Show[
 Plot[{res[[1]][t, 1.25, .25], outsideTemp[t], 18, 20}, {t, 0, 
   2*24}], hp]

Out[6]=