Study the Formation of a Shock Wave

Use Burgers' equation for viscous fluid flow to study the formation of a shock wave.

In[1]:=

TraditionalForm[BurgersEquation = \!\( \*SubscriptBox[\(\[PartialD]\), \({t}\)]\(u[x, t]\)\) + u[x, t] \!\( \*SubscriptBox[\(\[PartialD]\), \({x}\)]\(u[x, t]\)\) == \[Epsilon] \!\( \*SubscriptBox[\(\[PartialD]\), \({x, 2}\)]\(u[x, t]\)\)]

Out[1]//TraditionalForm=

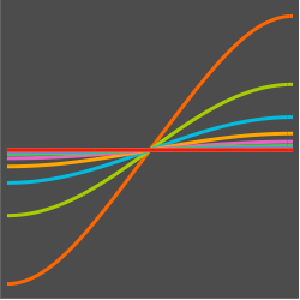
Prescribe a piecewise initial condition.

In[2]:=

InitialCondition = u[x, 0] == Piecewise[{{1, x < 0}}];

Solve the initial value problem.

In[3]:=

dsol = DSolveValue[{BurgersEquation, InitialCondition}, u[x, t], {x, t}]

Out[3]=

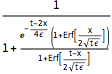
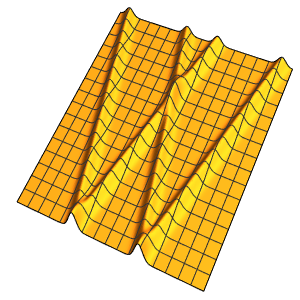
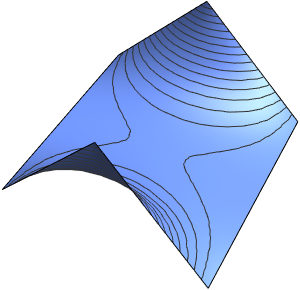
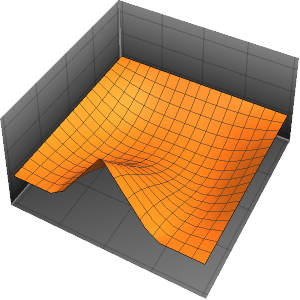
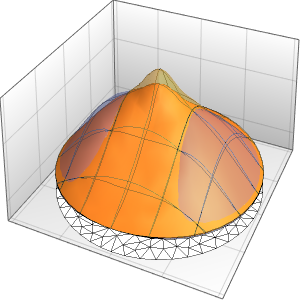
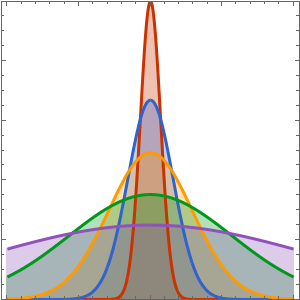
The solution is smooth for any positive value of ϵ.

In[4]:=

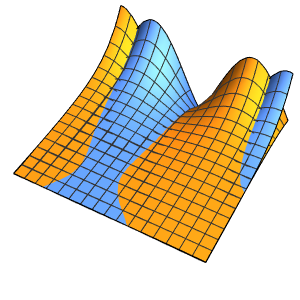
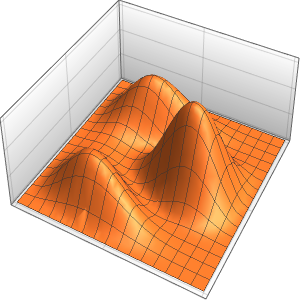
Plot3D[dsol /. {\[Epsilon] -> 1/10}, {x, -2, 2}, {t, 0.001, 5}]

Out[4]=

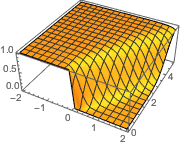
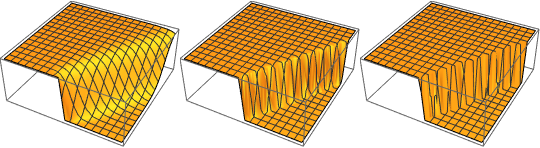
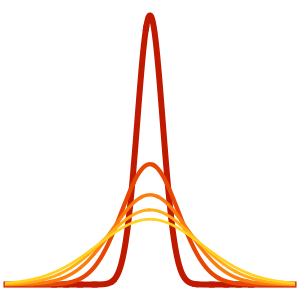
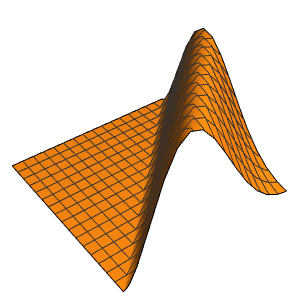
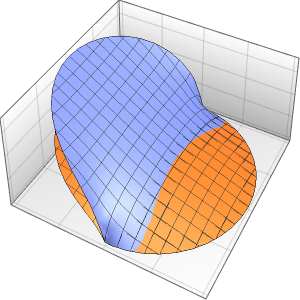
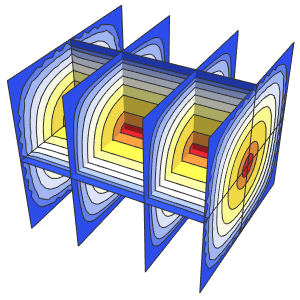
The solution develops a shock discontinuity in the limit when ϵ approaches 0.

In[5]:=

Row[Table[Plot3D[dsol, {x, -2, 2}, {t, 0.001, 5}, Exclusions -> None, Ticks -> None], {\[Epsilon], {1/10, 1/100, 1/1000}}]]

Out[5]=