Wolfram言語™

数量を含む打切り分布

アメリカ合衆国の成人男性の体重は，平均体重191ポンド，標準偏差70ポンドの正規分布でモデル化できる．家庭用の体重計で測れる最大体重が300ポンドであるとして，一般的な家庭用の体重計で測った体重の分布を求める．

In[1]:=

\[ScriptCapitalD] = CensoredDistribution[{Quantity[0, "Pounds"], Quantity[300, "Pounds"]}, \[ScriptD] = NormalDistribution[Quantity[191, "Pounds"], Quantity[70, "Pounds"]]]

Out[1]=

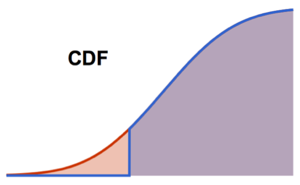
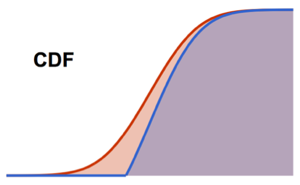
累積分布関数．

In[2]:=

Plot[CDF[\[ScriptCapitalD], Quantity[x, "Pounds"]] // Evaluate, {x, 0, 350}, Filling -> Axis, Exclusions -> None, AxesLabel -> {"lb"}]

Out[2]=

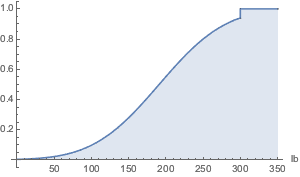
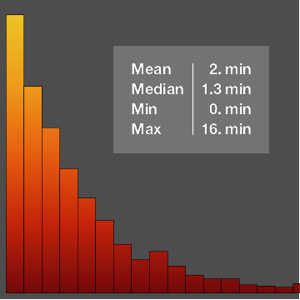
打切りがもとの分布の打切りよりも低いと仮定した場合の平均体重．

In[3]:=

{Mean[\[ScriptCapitalD]], Mean[\[ScriptD]]} // N

Out[3]=

打切り分布による体重の中央値は，もとの分布による体重の中央値と同じである．

In[4]:=

{Median[\[ScriptCapitalD]], Median[\[ScriptD]]}

Out[4]=