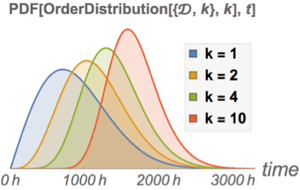
Случайные векторы с различными единицами
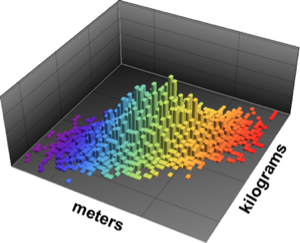
Определим совместное распределение роста и веса с предполагаемой корреляцией 0,65 между этими величинами.
In[1]:=
hw\[ScriptCapitalD] =
BinormalDistribution[{Quantity[1.8, "Meters"],
Quantity[85, "Kilograms"]}, {Quantity[0.15, "Meters"],
Quantity[9, "Kilograms"]}, 0.65]Out[1]=
Рассчитaeм вероятность того, что рост человека превысит 1,75 метра , учитывая, что вес человека больше 72 килограммов.
In[2]:=
NProbability[
h > Quantity[1.75, "m"] \[Conditioned]
w > Quantity[72, "kg"], {h, w} \[Distributed] hw\[ScriptCapitalD]]Out[2]=
Рассчитaeм распределение индекса массы тела (ИМТ) для заданной выборки населения.
In[3]:=
bmi\[ScriptCapitalD] =
TransformedDistribution[
w/h^2, {h, w} \[Distributed] hw\[ScriptCapitalD]]Out[3]=
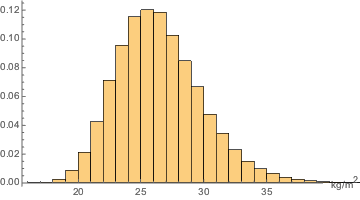
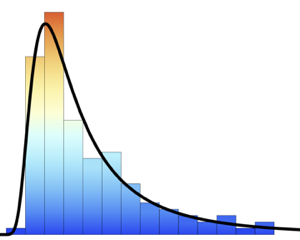
Рассчитaeм распределение индекса массы тела с использованием выборочной гистограммы.
In[4]:=
sample = RandomVariate[bmi\[ScriptCapitalD], 10^5];
Histogram[sample, Automatic, "PDF", AxesLabel -> Automatic]Out[4]=