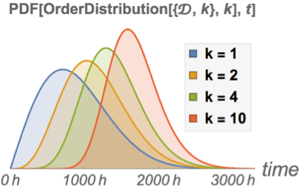
Цензурированнoe распределениe с величинами
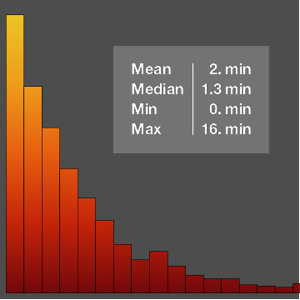
Масса тела взрослых мужчин в США моделируется с нормальным распределением со средним значением 191 фунтов и стандартным отклонением 70 фунтов. Если предположить, что весы для ванной комнаты имеют верхний предел в 300 фунтов, найдем распределение веса измеренного с помощью обычных весов для ванной комнаты.
In[1]:=
\[ScriptCapitalD] =
CensoredDistribution[{Quantity[0, "Pounds"],
Quantity[300, "Pounds"]}, \[ScriptD] =
NormalDistribution[Quantity[191, "Pounds"],
Quantity[70, "Pounds"]]]Out[1]=
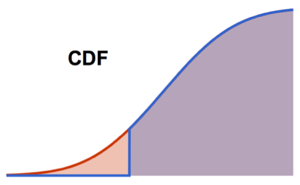
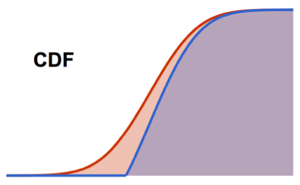
Рассчитаем кумулятивную функцию распределения.
In[2]:=
Plot[CDF[\[ScriptCapitalD], Quantity[x, "Pounds"]] // Evaluate, {x, 0,
350}, Filling -> Axis, Exclusions -> None, AxesLabel -> {"lb"}]Out[2]=
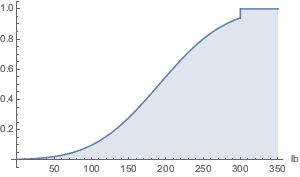
Средний вес, с учетом усечения, ниже, чем у исходного распределения.
In[3]:=
{Mean[\[ScriptCapitalD]], Mean[\[ScriptD]]} // NOut[3]=
Медиана веса, с учетом усечения, такая же, как у исходного распределения.
In[4]:=
{Median[\[ScriptCapitalD]], Median[\[ScriptD]]}Out[4]=