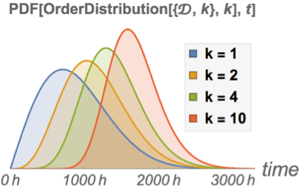
Распределение с количественными параметрами

Приблизим распределение по высоте к нормальному распределению со средним значением 70 дюймов и стандартным отклонением 6,5 дюймов. Данное распределение может быть построено с использованием Quantity в качестве соответствующих параметров среднего значения и стандартного отклонения и даст соответствующее распределение QuantityDistribution.

In[1]:=

height\[ScriptCapitalD] = NormalDistribution[Quantity[70, "Inches"], Quantity[6.5, "Inches"]]

Out[1]=

Распределение представляет собой случайную величину, выраженную в указанных единицах.

In[2]:=

averageHeight = Mean[height\[ScriptCapitalD]]

Out[2]=

Рассчитаем распределение человеческого роста с использованием заданных количественных величин.

In[3]:=

CDF[height\[ScriptCapitalD], Quantity[170, "Centimeters"]]

Out[3]=

Рассчитаем вероятность того, что рост человека составляет величину между 65 и 72 дюймами.

In[4]:=

Probability[Quantity[65, "in"] < x < Quantity[72, "in"], x \[Distributed] height\[ScriptCapitalD]]

Out[4]=

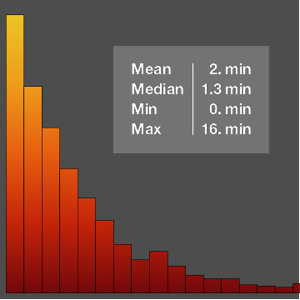
Используя заданное распределение роста, рассчитаем среднее время падения шляпы с головы человека на платене Земля.

In[5]:=

NExpectation[Sqrt[(2 h)/Entity["Planet", "Earth"]["Gravity"]], h \[Distributed] height\[ScriptCapitalD]]

Out[5]=