Étudiez les propriétés des étoiles : Nouveautés de Wolfram Language 11

Étudiez les propriétés des étoiles

StarData donne accès à des propriétés de plus de 10⁵ étoiles. Sélectionnez un échantillon aléatoire de 3000 étoiles à étudier.

In[1]:=

stars = StarData[{"RandomEntities", 3000}];

Il existe de nombreuses propriétés fournies pour chacune des entités.

In[2]:=

sun = \!\(\*
NamespaceBox["LinguisticAssistant",
DynamicModuleBox[{Typeset`query$$ = "Sun", Typeset`boxes$$ = 
      TemplateBox[{"\"Sun\"", 
RowBox[{"Entity", "[", 
RowBox[{"\"Star\"", ",", "\"Sun\""}], "]"}], 
        "\"Entity[\\\"Star\\\", \\\"Sun\\\"]\"", "\"star\""}, 
       "Entity"], 
      Typeset`allassumptions$$ = {{
       "type" -> "Clash", "word" -> "Sun", 
        "template" -> "Assuming \"${word}\" is ${desc1}. Use as \
${desc2} instead", "count" -> "4", 
        "Values" -> {{
          "name" -> "Star", "desc" -> " referring to stars", 
           "input" -> "*C.Sun-_*Star-"}, {
          "name" -> "CalendarEventName", "desc" -> "a weekday", 
           "input" -> "*C.Sun-_*CalendarEventName-"}, {
          "name" -> "Word", "desc" -> "a word", 
           "input" -> "*C.Sun-_*Word-"}, {
          "name" -> "Surname", "desc" -> "a surname", 
           "input" -> "*C.Sun-_*Surname-"}}}}, 
      Typeset`assumptions$$ = {}, Typeset`open$$ = {1, 2}, 
      Typeset`querystate$$ = {
      "Online" -> True, "Allowed" -> True, 
       "mparse.jsp" -> 1.321761`6.572697926887039, "Messages" -> {}}}, 
DynamicBox[ToBoxes[
AlphaIntegration`LinguisticAssistantBoxes["", 4, Automatic, 
Dynamic[Typeset`query$$], 
Dynamic[Typeset`boxes$$], 
Dynamic[Typeset`allassumptions$$], 
Dynamic[Typeset`assumptions$$], 
Dynamic[Typeset`open$$], 
Dynamic[Typeset`querystate$$]], StandardForm],
ImageSizeCache->{114., {7., 15.}},
TrackedSymbols:>{
        Typeset`query$$, Typeset`boxes$$, Typeset`allassumptions$$, 
         Typeset`assumptions$$, Typeset`open$$, Typeset`querystate$$}],
DynamicModuleValues:>{},
UndoTrackedVariables:>{Typeset`open$$}],
BaseStyle->{"Deploy"},
DeleteWithContents->True,
Editable->False,
SelectWithContents->True]\);

In[3]:=

StarData[sun, "Properties"] // Length

Out[3]=

Extrayez la température efficace pour la sélection aléatoire des étoiles et sélectionnez celles pour lesquelles les données sont disponibles.

In[4]:=

temps = Flatten[
   DeleteMissing[StarData[#, "EffectiveTemperature"]] & /@ 
    Partition[stars, 100]];

Calculez les statistiques descriptives des températures.

In[5]:=

stats = {Min, Max, Mean, Median, StandardDeviation};
TableForm[{Map[#[temps] &, stats]}, TableHeadings -> {None, stats}]

Out[5]//TableForm=

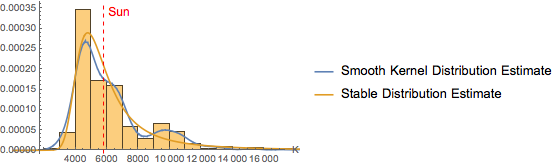
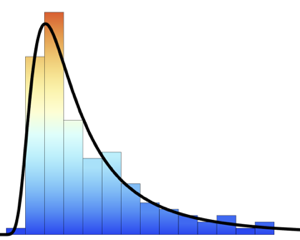
Tracez l'histogramme de la température de l'étoile.

In[6]:=

h = Histogram[temps, 25, PDF, AxesLabel -> Automatic]

Out[6]=

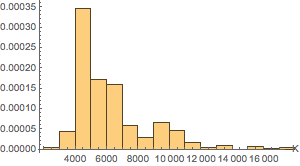
Estimez la répartition des températures au moyen d'une loi non paramétrique.

In[7]:=

skd = SmoothKernelDistribution[temps, "Oversmooth"]

Out[7]=

Estimez la répartition des températures par une loi paramétrique à longue queue.

In[8]:=

edist = EstimatedDistribution[temps, StableDistribution[a, b, c, d]]

Out[8]=

Comparez les estimations de la fonction de densité de probabilité et liez-les à la température du soleil.

Afficher l'entrée complète de Wolfram Language

In[9]:=

pdf = PDF[skd, Quantity[x, "Kelvins"]];
sunTemp = {Directive[Red, Dashed], 
   InfiniteLine[{{#, 0}, {#, 1}} &[
     QuantityMagnitude[sun["EffectiveTemperature"]]]]};
Show[h, Plot[{pdf, PDF[edist, Quantity[x, "Kelvins"]]}, {x, 0, 
   QuantityMagnitude@Max[temps]}, PlotRange -> All, 
  PlotLegends -> {"Smooth Kernel Distribution Estimate", 
    "Stable Distribution Estimate"}], 
 Epilog -> {sunTemp, Inset[Style["Sun", Red, 12], {6800, .00034}]}]

Out[9]=

Wolfram Language™

Étudiez les propriétés des étoiles

Exemples connexes