Vecteurs aléatoires avec des unités différentes
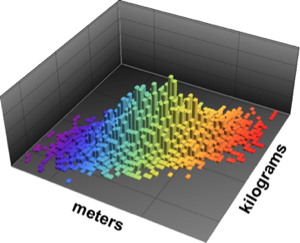
Définissez une répartition hauteur-poids conjointe avec corrélation supposée de 0,65.
In[1]:=
hw\[ScriptCapitalD] =
BinormalDistribution[{Quantity[1.8, "Meters"],
Quantity[85, "Kilograms"]}, {Quantity[0.15, "Meters"],
Quantity[9, "Kilograms"]}, 0.65]Out[1]=
Calculez la probabilité que la taille d'une personne soit supérieure à 1,75 mètre, étant donné que son poids est supérieur à 72 kilogrammes.
In[2]:=
NProbability[
h > Quantity[1.75, "m"] \[Conditioned]
w > Quantity[72, "kg"], {h, w} \[Distributed] hw\[ScriptCapitalD]]Out[2]=
Calculez la loi de l'indice de masse corporelle (IMC) pour la population supposée.
In[3]:=
bmi\[ScriptCapitalD] =
TransformedDistribution[
w/h^2, {h, w} \[Distributed] hw\[ScriptCapitalD]]Out[3]=
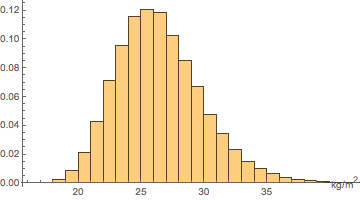
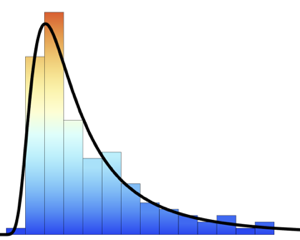
Estimez la répartition de l'IMC à l'aide d'un échantillon d'histogramme.
In[4]:=
sample = RandomVariate[bmi\[ScriptCapitalD], 10^5];
Histogram[sample, Automatic, "PDF", AxesLabel -> Automatic]Out[4]=