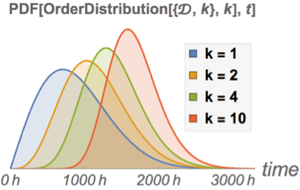
Distributions non paramétriques des données de grandeurs
Utilisez WeatherData pour obtenir des séries temporelles de mesures de vitesse du vent dans la ville de Chicago depuis le début de l'année 2014 jusqu'à la fin de 2015.
In[1]:=
wsts = WeatherData["Chicago",
"WindSpeed", {DateObject[{2014, 1, 1}], DateObject[{2015, 12, 31}]}]Out[1]=
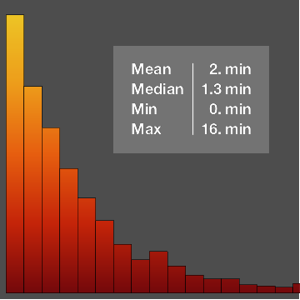
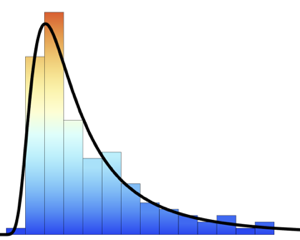
Utilisez Histogram pour visualiser la répartition de la vitesse du vent.
In[2]:=
Histogram[wsts, PlotTheme -> "Detailed", FrameLabel -> Automatic]Out[2]=
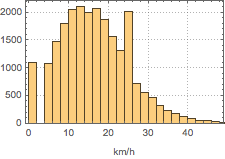
Extrayez les valeurs de la vitesse du vent avec les valeurs manquantes interpolées.
In[3]:=
winds = Values[TimeSeries[wsts, MissingDataMethod -> "Interpolation"]]Out[3]=
Utilisez SmoothKernelDistribution pour construire le modèle non paramétrique des vitesses du vent à Chicago, en veillant à ce que la vitesse du vent reste non négative.
In[4]:=
ws\[ScriptCapitalD] =
SmoothKernelDistribution[winds,
Automatic, {"Bounded", Quantity[0, ("Kilometers")/("Hours")],
"Gaussian"}]Out[4]=
Utilisez un modèle non paramétrique de puissance de sortie de la turbine en fonction de la vitesse du vent pour estimer la puissance moyenne pour un GE de 1,5 MW turbine éolienne installée à cet endroit.
In[5]:=
turbine =
Interpolation[
QuantityArray[{{0.`, 0.`}, {0.5`, 0.`}, {1.`, 0.`}, {1.5`,
0.`}, {2.`, 0.`}, {2.5`, 0.`}, {3.`, 0.`}, {3.5`, 0.`}, {4.`,
36.`}, {4.5`, 66.`}, {5.`, 104.`}, {5.5`, 150.`}, {6.`,
205.`}, {6.5`, 269.`}, {7.`, 344.`}, {7.5`, 428.`}, {8.`,
528.`}, {8.5`, 644.`}, {9.`, 774.`}, {9.5`, 926.5`}, {10.`,
1079.`}, {10.5`, 1211.`}, {11.`, 1342.`}, {11.5`,
1401.`}, {12.`, 1460.`}, {12.5`, 1477.`}, {13.`,
1494.`}, {13.5`, 1500.`}, {30.`, 1500.`}}, {"Meters"/"Seconds",
"Kilowatts"}] // Normal, InterpolationOrder -> 1];In[6]:=
NExpectation[turbine[v], v \[Distributed] ws\[ScriptCapitalD]]Out[6]=
