Loi tronquée avec des grandeurs

Le diamètre d'une canneberge américaine suit une loi normale avec une moyenne de 16 mm et un écart-type de 1,6 mm. Un fruit doit avoir un diamètre d'au moins 15 mm pour être vendu entier ; sinon, il est utilisé pour la production de sauce aux airelles. Trouvez la répartition de la taille des fruits vendus entiers.

In[1]:=

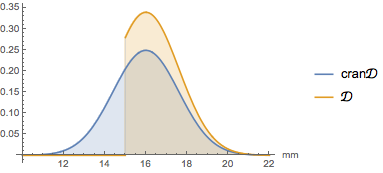
cran\[ScriptCapitalD] = NormalDistribution[Quantity[16, "Millimeters"], Quantity[1.6, "Millimeters"]]; \[ScriptCapitalD] = TruncatedDistribution[{Quantity[15, "Millimeters"], \[Infinity]}, cran\[ScriptCapitalD]];

Comparez les fonctions de densité de probabilité.

In[2]:=

Plot[{PDF[cran\[ScriptCapitalD], Quantity[x, "Milimeters"]], PDF[\[ScriptCapitalD], Quantity[x, "Milimeters"]]}, {x, 10, 22}, PlotLegends -> {"cran\[ScriptCapitalD]", "\[ScriptCapitalD]"}, Filling -> Axis, AxesLabel -> {"mm"}]

Out[2]=

En supposant qu'un paquet d'une livre de canneberges a un volume d'environ 30 in³, trouvez les limites moyennes inférieures et supérieures pour le nombre de canneberges dans un tel paquet.

In[3]:=

lowerbound = Floor[NExpectation[ Divide[Quantity[30, "Inches"^3], Volume[Cuboid[{0, 0, 0}, {x, x, x}]]], x \[Distributed] \[ScriptCapitalD]]]

Out[3]=

In[4]:=

upperbound = Ceiling[NExpectation[ Divide[Quantity[30, "Inches"^3], Volume[Ball[{0, 0, 0}, x/2]]], x \[Distributed] \[ScriptCapitalD]]]

Out[4]=