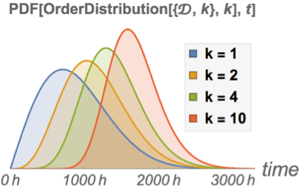
Усечённое распределение с величинами
Диаметр американской клюквы имеет нормальное распределение со средним значением в 16 мм и стандартным отклонением в 1,6 мм. Плоды должны быть не менее 15 мм в диаметре, чтобы поступить в продажу; в противном случае плоды используются для производства клюквенного соуса. Найдем распределение размера плодов клюквы поступающих в продажу (не в качестве соуса).
In[1]:=
cran\[ScriptCapitalD] =
NormalDistribution[Quantity[16, "Millimeters"],
Quantity[1.6, "Millimeters"]];
\[ScriptCapitalD] =
TruncatedDistribution[{Quantity[15, "Millimeters"], \[Infinity]},
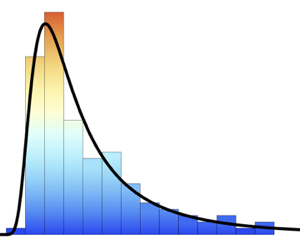
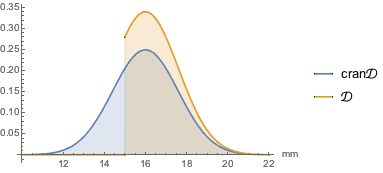
cran\[ScriptCapitalD]];Сравним функции плотности вероятности.
In[2]:=

Plot[{PDF[cran\[ScriptCapitalD], Quantity[x, "Milimeters"]],
PDF[\[ScriptCapitalD], Quantity[x, "Milimeters"]]}, {x, 10, 22},
PlotLegends -> {"cran\[ScriptCapitalD]", "\[ScriptCapitalD]"},
Filling -> Axis, AxesLabel -> {"mm"}]Out[2]=
Если предположить, что одна упаковка клюквы весом в 1 фунт имеет объем около 30 кубических унций, рассчитаем средние нижние и верхние показатели количества ягод в такой упаковке.
In[3]:=

lowerbound =
Floor[NExpectation[
Divide[Quantity[30, "Inches"^3],
Volume[Cuboid[{0, 0, 0}, {x, x, x}]]],
x \[Distributed] \[ScriptCapitalD]]]Out[3]=
In[4]:=

upperbound =
Ceiling[NExpectation[
Divide[Quantity[30, "Inches"^3], Volume[Ball[{0, 0, 0}, x/2]]],
x \[Distributed] \[ScriptCapitalD]]]Out[4]=