수량을 포함하는 절단 분포

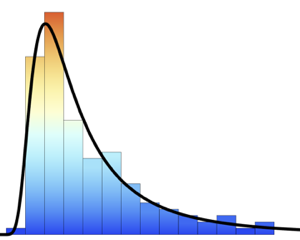
미국 크랜베리의 직경은 평균 16mm, 표준 편차 1.6mm의 정규 분포를 따릅니다. 열매는 지름이 최소 15mm 이상일때만 열매 그대로의 형태로 판매 할 수 있습니다. 그렇지 않은 경우, 작은 크기의 열매는 크랜베리 소스 생산에 사용됩니다. 열매 그대로의 형태로 판매되는 과일의 크기 분포를 구합니다.

In[1]:=

cran\[ScriptCapitalD] = NormalDistribution[Quantity[16, "Millimeters"], Quantity[1.6, "Millimeters"]]; \[ScriptCapitalD] = TruncatedDistribution[{Quantity[15, "Millimeters"], \[Infinity]}, cran\[ScriptCapitalD]];

확률 밀도 함수를 비교합니다.

In[2]:=

Plot[{PDF[cran\[ScriptCapitalD], Quantity[x, "Milimeters"]], PDF[\[ScriptCapitalD], Quantity[x, "Milimeters"]]}, {x, 10, 22}, PlotLegends -> {"cran\[ScriptCapitalD]", "\[ScriptCapitalD]"}, Filling -> Axis, AxesLabel -> {"mm"}]

Out[2]=

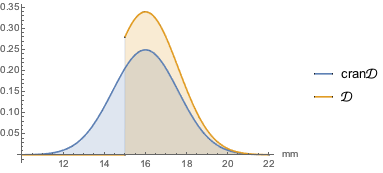
1 파운드 패키지 크랜베리는 용량이 약 30in³이므로, 한 패키지에 들어있는 크랜베리 수의 상한과 하한의 평균을 구합니다.

In[3]:=

lowerbound = Floor[NExpectation[ Divide[Quantity[30, "Inches"^3], Volume[Cuboid[{0, 0, 0}, {x, x, x}]]], x \[Distributed] \[ScriptCapitalD]]]

Out[3]=

In[4]:=

upperbound = Ceiling[NExpectation[ Divide[Quantity[30, "Inches"^3], Volume[Ball[{0, 0, 0}, x/2]]], x \[Distributed] \[ScriptCapitalD]]]

Out[4]=