Wolfram言語™

映画学を極める

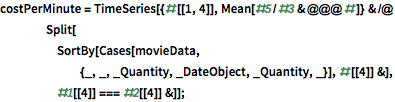
2000年以降にリリースされた映画の1分ごとのコストと興行収入をWolfram Knowledgebaseを使って計算する．次に，これらの映画の平均上映時間も求める．上映時間は，人工のものにしては珍しく，いわゆる安定分布法に従っている．

隠的に定義された実体クラスを使って，世紀の変わり目以降にリリースされた映画を選択する．

In[1]:=

Length[movies = EntityClass["Movie", EntityProperty["Movie", "ReleaseDate"] -> Between[{DateObject[{2000}], DateObject[{2015}]}]] // EntityList]

Out[1]=

映画のタイトル，ジャンル，上映時間，制作費，興行収入を取得する．

In[2]:=

movieData = EntityValue[ movies, {EntityProperty["Movie", "Name"], EntityProperty["Movie", "Genres"], EntityProperty["Movie", "Runtime"], EntityProperty["Movie", "ReleaseDate"], EntityProperty["Movie", "ProductionBudget"], EntityProperty["Movie", "DomesticBoxOfficeGross"]}];

リリースされた映画の1分あたりのコストは，時間とともに大きく変動する．

In[3]:=

costPerMinute = TimeSeries[{#[[1, 4]], Mean[#5/#3 & @@@ #]} & /@ Split[SortBy[ Cases[movieData, {_, _, _Quantity, _DateObject, _Quantity, _}], \ #[[4]] &], #1[[4]] === #2[[4]] &]];

In[4]:=

DateListLogPlot[costPerMinute, FrameLabel -> Automatic, PlotLabel -> "average cost per minute", AxesOrigin -> {DateObject[{2000, 1, 1}], 0}]

Out[4]=

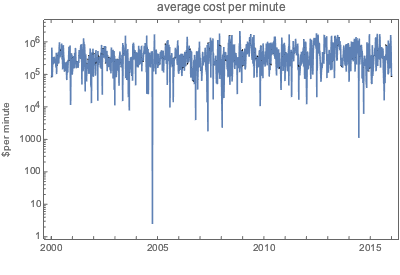
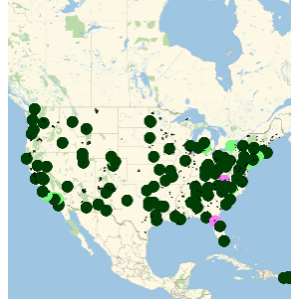
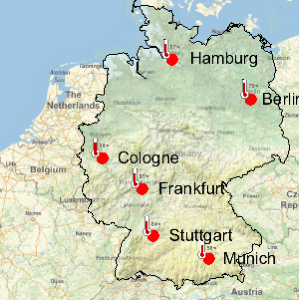
1ヶ月ごとの平均を求めると，1分あたりのコストの周期性が見えるようになる．以下のプロットでは，緑の格子線が独立記念日を，紫の線が感謝祭を示している．

In[5]:=

DateListPlot[MovingAverage[costPerMinute, Quantity[1, "Months"]], FrameLabel -> Automatic, PlotLabel -> "average cost per minute", AxesOrigin -> {DateObject[{2000, 1, 1}], 0}, GridLines -> {Join[{#, Darker[Green]} & /@ Table[DateObject[{y, 7, 4}], {y, 2000, 2015}], {#, Darker[Purple]} & /@ Table[DateObject@ WolframAlpha[ "Thanksgiving " <> IntegerString[y], {{"Result", 1}, "ComputableData"}], {y, 2000, 2015}]], None}]

Out[5]=

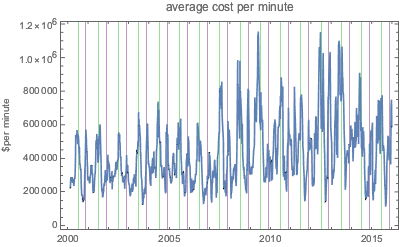
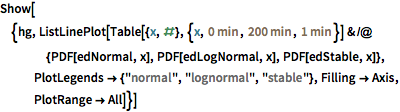
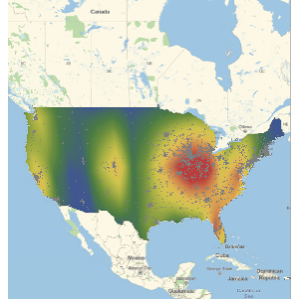
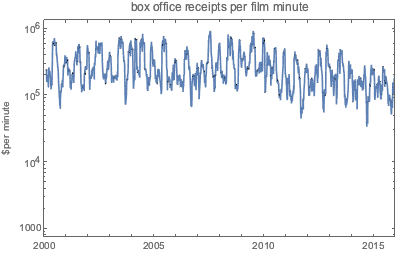
次の対数プロットで分かるように，1分あたりの興行収入は，1分あたりのコスト以上に激しく変動する関数である．

In[6]:=

profitPerMinute = TimeSeries[{#[[1, 4]], Mean[#6/#3 & @@@ #]} & /@ Split[SortBy[ Cases[movieData, {_, _, _Quantity, _DateObject, _, _Quantity}], \ #[[4]] &], #1[[4]] === #2[[4]] &]];

In[7]:=

DateListLogPlot[MovingAverage[profitPerMinute, Quantity[1, "Months"]], FrameLabel -> Automatic, PlotLabel -> "box office receipts per film minute", AxesOrigin -> {DateObject[{2000, 1, 1}], 0}, PlotRange -> {{DateObject[{2000, 1, 1}], DateObject[{2015, 12, 31}]}, All}]

Out[7]=

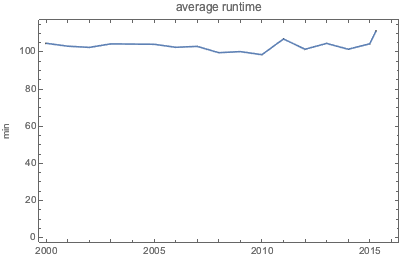
映画の平均上映時間は過去15年間に渡ってかなり一定している．

In[8]:=

averageRuntimes = {#[[1, 1]], Mean[#[[All, -1]]]} & /@ Split[Sort[{DateObject[{#4["Year"]}], UnitConvert[#3, "Minutes"]} & @@@ Cases[movieData, {_, _, _Quantity, _DateObject, _, _}]], #1[[ 1]] === #2[[1]] &];

In[9]:=

DateListPlot[averageRuntimes, FrameLabel -> Automatic, PlotLabel -> "average runtime", AxesOrigin -> {DateObject[{2000, 1, 1}], 0}]

Out[9]=

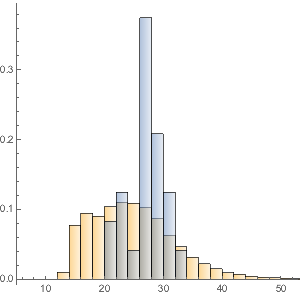
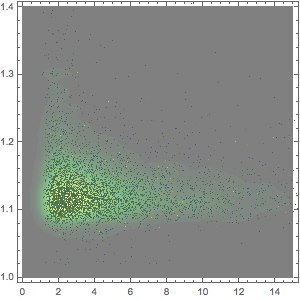
より詳しく見ると，映画の上映時間の分布は比較的滑らかなように見える．

In[10]:=

movieRuntimes = DeleteMissing[movieData[[All, 3]]];

In[11]:=

hg = Histogram[movieRuntimes, {1, 200, 5}, "PDF", AxesLabel -> Automatic]

Out[11]=

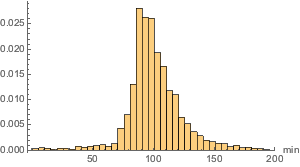
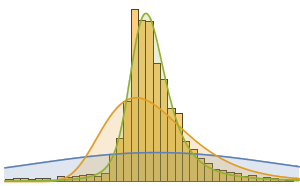
数多くの組込み分布を使ってモデル化してみると，最も近いフィットがLévy安定分布によってもたらされることが分かる．ここで，正規分布（独立分布から独立して取り出された確率変数の平均の分布），対数正規分布（独立した多くの正の確率変数の乗積の分布），安定分布を使ったフィットを計算する．

In[12]:=

edNormal = EstimatedDistribution[movieRuntimes, NormalDistribution[\[Mu], \[Sigma]]]

Out[12]=

In[13]:=

edLogNormal = EstimatedDistribution[movieRuntimes, LogNormalDistribution[\[Mu], \[Sigma]]]

Out[13]=

In[14]:=

edStable = EstimatedDistribution[movieRuntimes, StableDistribution[1, \[Alpha], \[Beta], \[Mu], \[Sigma]]]

Out[14]=

おもしろいことに，視覚的には安定分布が最もよくフィットする．

In[15]:=

Show[{hg, ListLinePlot[ Table[{x, #}, {x, Quantity[0, "Minutes"], Quantity[200, "Minutes"], Quantity[1, "Minutes"]}] & /@ {PDF[edNormal, x], PDF[edLogNormal, x], PDF[edStable, x]}, PlotLegends -> {"normal", "lognormal", "stable"}, Filling -> Axis, PlotRange -> All]}]

Out[15]=

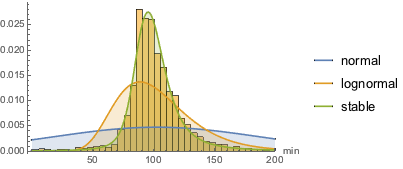
人工のもので安定分布に従うものは少ない．安定分布の特徴の一つは，比較的大きい（しばしば平均の数倍の）外れ値を含むことである．この特徴は映画では実現されている．ここでは，隠的に定義された実体クラスを使って2000年1月1日以降にリリースされた（上演時間が）最長の10の映画が選ばれている．

In[16]:=

longest = EntityClass[ "Movie", {EntityProperty["Movie", "ReleaseDate"] -> Between[{DateObject[{2000}], DateObject[{2015}]}], EntityProperty["Movie", "Runtime"] -> TakeLargest[10]}] // EntityList

Out[16]=

表にまとめる．

In[17]:=

With[{props = {EntityProperty["Movie", "Name"], EntityProperty["Movie", "Genres"], EntityProperty["Movie", "Runtime"], EntityProperty["Movie", "ReleaseDate"]}}, TextGrid[Prepend[EntityValue[longest, props], props], Dividers -> All, Alignment -> Left, Background -> {None, {LightBlue}}]] // TraditionalForm

Out[17]//TraditionalForm=