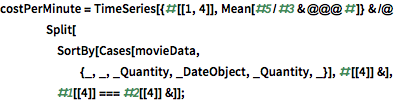
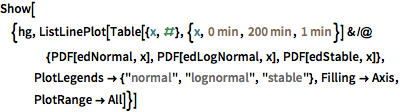
Explore o mundo do cinema

Utilize a Wolfram Knowledgebase para estudar o custo por minuto e a receita de bilheteria para filmes laçados a partir do ano 2000. Além disso, explore o tempo médio de projeção desses filmes, que, raramente entre os objetos feitos pelo homem, parece seguir a chamada lei de distribuição estável.

Use uma classe de entidade implicitamente definida para selecionar os filmes lançados desde a virada do milênio.

In[1]:=

Length[movies = EntityClass["Movie", EntityProperty["Movie", "ReleaseDate"] -> Between[{DateObject[{2000}], DateObject[{2015}]}]] // EntityList]

Out[1]=

Extraia os títulos dos filmes, gêneros, durações, orçamentos de produção, e os totais de bilheteria.

In[2]:=

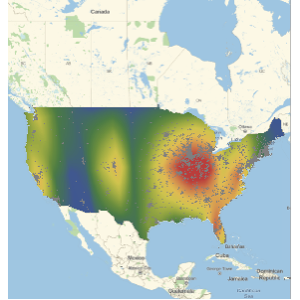
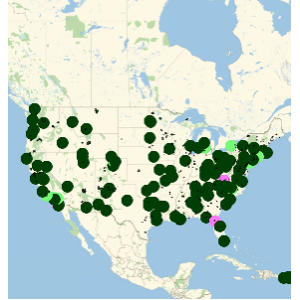
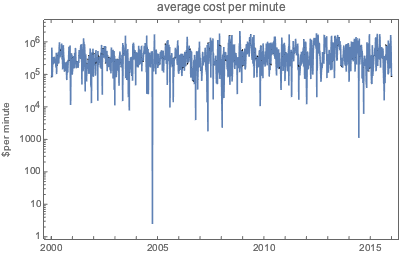
movieData = EntityValue[ movies, {EntityProperty["Movie", "Name"], EntityProperty["Movie", "Genres"], EntityProperty["Movie", "Runtime"], EntityProperty["Movie", "ReleaseDate"], EntityProperty["Movie", "ProductionBudget"], EntityProperty["Movie", "DomesticBoxOfficeGross"]}];

O custo por minuto de um filme lançado é uma função altamente flutuante ao longo do tempo.

In[3]:=

costPerMinute = TimeSeries[{#[[1, 4]], Mean[#5/#3 & @@@ #]} & /@ Split[SortBy[ Cases[movieData, {_, _, _Quantity, _DateObject, _Quantity, _}], \ #[[4]] &], #1[[4]] === #2[[4]] &]];

In[4]:=

DateListLogPlot[costPerMinute, FrameLabel -> Automatic, PlotLabel -> "average cost per minute", AxesOrigin -> {DateObject[{2000, 1, 1}], 0}]

Out[4]=

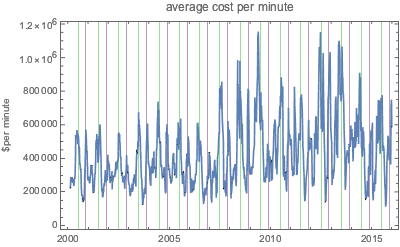
No entanto, na média de um mês, alguns custos com periodicidade por minuto tornam-se visíveis. Em particular, as linhas verdes mostram o Quatro de Julho e as linhas roxas o Dia de Ação de Graças no gráfico abaixo.

In[5]:=

DateListPlot[MovingAverage[costPerMinute, Quantity[1, "Months"]], FrameLabel -> Automatic, PlotLabel -> "average cost per minute", AxesOrigin -> {DateObject[{2000, 1, 1}], 0}, GridLines -> {Join[{#, Darker[Green]} & /@ Table[DateObject[{y, 7, 4}], {y, 2000, 2015}], {#, Darker[Purple]} & /@ Table[DateObject@ WolframAlpha[ "Thanksgiving " <> IntegerString[y], {{"Result", 1}, "ComputableData"}], {y, 2000, 2015}]], None}]

Out[5]=

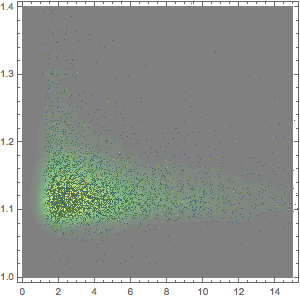
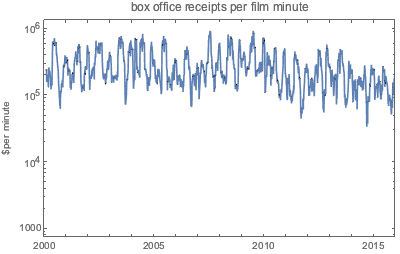
Conforme mostra o gráfico logarítmico abaixo, as receitas de bilheteria por minuto são uma função ainda mais flutuante.

In[6]:=

profitPerMinute = TimeSeries[{#[[1, 4]], Mean[#6/#3 & @@@ #]} & /@ Split[SortBy[ Cases[movieData, {_, _, _Quantity, _DateObject, _, _Quantity}], \ #[[4]] &], #1[[4]] === #2[[4]] &]];

In[7]:=

DateListLogPlot[MovingAverage[profitPerMinute, Quantity[1, "Months"]], FrameLabel -> Automatic, PlotLabel -> "box office receipts per film minute", AxesOrigin -> {DateObject[{2000, 1, 1}], 0}, PlotRange -> {{DateObject[{2000, 1, 1}], DateObject[{2015, 12, 31}]}, All}]

Out[7]=

O tempo de projeção médio dos filmes tem sido bastante consistente ao longo dos últimos 15 anos.

In[8]:=

averageRuntimes = {#[[1, 1]], Mean[#[[All, -1]]]} & /@ Split[Sort[{DateObject[{#4["Year"]}], UnitConvert[#3, "Minutes"]} & @@@ Cases[movieData, {_, _, _Quantity, _DateObject, _, _}]], #1[[ 1]] === #2[[1]] &];

In[9]:=

DateListPlot[averageRuntimes, FrameLabel -> Automatic, PlotLabel -> "average runtime", AxesOrigin -> {DateObject[{2000, 1, 1}], 0}]

Out[9]=

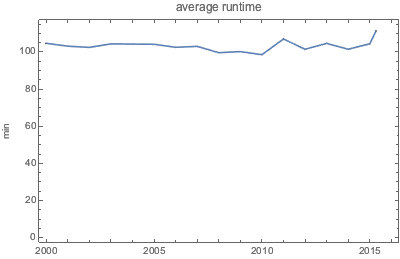
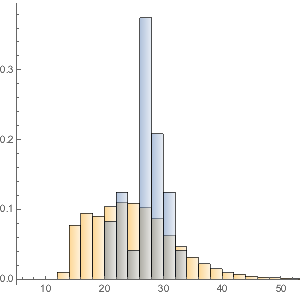
Vendo com mais detalhe, a distribuição das projeções de filmes parace ser relativamente suave.

In[10]:=

movieRuntimes = DeleteMissing[movieData[[All, 3]]];

In[11]:=

hg = Histogram[movieRuntimes, {1, 200, 5}, "PDF", AxesLabel -> Automatic]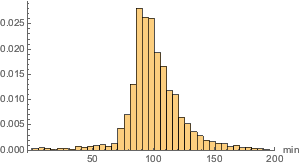

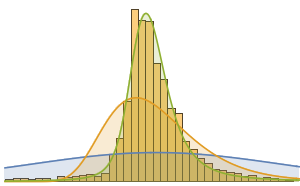
Out[11]=

Modelar usando um grande número de distribuições integradas indica que o ajuste mais próximo é fornecido por uma distribuição estável de Lévy. Aqui, ajuste usando uma normal (distribuição das médias de variáveis aleatórias feita de forma independente a partir de distribuições independentes), lognormal (a distribuição do produto multiplicativo de muitas variáveis aleatórias positivas independentes), e uma distribuição estável são calculados.

In[12]:=

edNormal = EstimatedDistribution[movieRuntimes, NormalDistribution[\[Mu], \[Sigma]]]

Out[12]=

In[13]:=

edLogNormal = EstimatedDistribution[movieRuntimes, LogNormalDistribution[\[Mu], \[Sigma]]]

Out[13]=

In[14]:=

edStable = EstimatedDistribution[movieRuntimes, StableDistribution[1, \[Alpha], \[Beta], \[Mu], \[Sigma]]]

Out[14]=

Curiosamente, a distribuição estável é visualmente o melhor ajuste.

In[15]:=

Show[{hg, ListLinePlot[ Table[{x, #}, {x, Quantity[0, "Minutes"], Quantity[200, "Minutes"], Quantity[1, "Minutes"]}] & /@ {PDF[edNormal, x], PDF[edLogNormal, x], PDF[edStable, x]}, PlotLegends -> {"normal", "lognormal", "stable"}, Filling -> Axis, PlotRange -> All]}]

Out[15]=

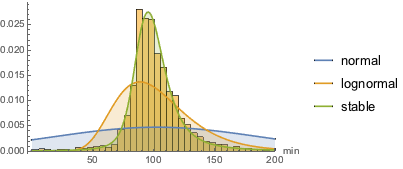
Apenas alguns objetos feitos pelo homem obedecem a uma distribuição estável. Uma característica de uma distribuição estável é a ocorrência de valores atípicos relativamente grandes, normalmente algumas vezes maiores do que a média. Esta característica é observada em filmes. Aqui, uma classe de entidade definida implicitamente é usada para selecionar os 10 mais longos (por tempo de projeção) filmes lançados após 1 de Janeiro de 2.000.

In[16]:=

longest = EntityClass[ "Movie", {EntityProperty["Movie", "ReleaseDate"] -> Between[{DateObject[{2000}], DateObject[{2015}]}], EntityProperty["Movie", "Runtime"] -> TakeLargest[10]}] // EntityList

Out[16]=

Faça um resumo em uma tabela.

In[17]:=

With[{props = {EntityProperty["Movie", "Name"], EntityProperty["Movie", "Genres"], EntityProperty["Movie", "Runtime"], EntityProperty["Movie", "ReleaseDate"]}}, TextGrid[Prepend[EntityValue[longest, props], props], Dividers -> All, Alignment -> Left, Background -> {None, {LightBlue}}]] // TraditionalForm

Out[17]//TraditionalForm=