Wolfram 语言™

探索电影科学

使用 Wolfram Knowledgebase 研究2000年以来上映电影的每分钟投入和票房收入. 另外，探索这些电影的平均播放时间，它被发现遵循所谓的稳定分布规律，这在人工对象中并不常见.

使用一个隐式定义的实体类中选择从两千年以来上映的电影.

In[1]:=

Length[movies = EntityClass["Movie", EntityProperty["Movie", "ReleaseDate"] -> Between[{DateObject[{2000}], DateObject[{2015}]}]] // EntityList]

Out[1]=

提取电影的片名、分类、播放时间、拍摄预算和票房总数.

In[2]:=

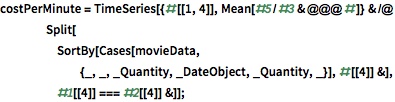
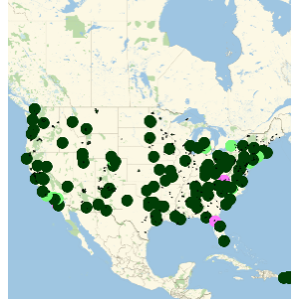
movieData = EntityValue[ movies, {EntityProperty["Movie", "Name"], EntityProperty["Movie", "Genres"], EntityProperty["Movie", "Runtime"], EntityProperty["Movie", "ReleaseDate"], EntityProperty["Movie", "ProductionBudget"], EntityProperty["Movie", "DomesticBoxOfficeGross"]}];

每分钟的票房收入是随时间剧烈波动的函数.

In[3]:=

costPerMinute = TimeSeries[{#[[1, 4]], Mean[#5/#3 & @@@ #]} & /@ Split[SortBy[ Cases[movieData, {_, _, _Quantity, _DateObject, _Quantity, _}], \ #[[4]] &], #1[[4]] === #2[[4]] &]];

In[4]:=

DateListLogPlot[costPerMinute, FrameLabel -> Automatic, PlotLabel -> "average cost per minute", AxesOrigin -> {DateObject[{2000, 1, 1}], 0}]

Out[4]=

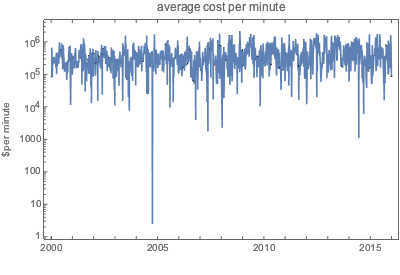
但是月平均上，一些每分钟费用的周期性变的明显. 具体而言，在下图中绿色网格线代表 7 月 4 日，紫色代表感恩节部分.

In[5]:=

DateListPlot[MovingAverage[costPerMinute, Quantity[1, "Months"]], FrameLabel -> Automatic, PlotLabel -> "average cost per minute", AxesOrigin -> {DateObject[{2000, 1, 1}], 0}, GridLines -> {Join[{#, Darker[Green]} & /@ Table[DateObject[{y, 7, 4}], {y, 2000, 2015}], {#, Darker[Purple]} & /@ Table[DateObject@ WolframAlpha[ "Thanksgiving " <> IntegerString[y], {{"Result", 1}, "ComputableData"}], {y, 2000, 2015}]], None}]

Out[5]=

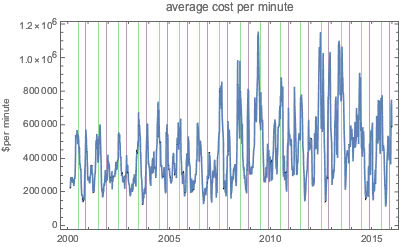
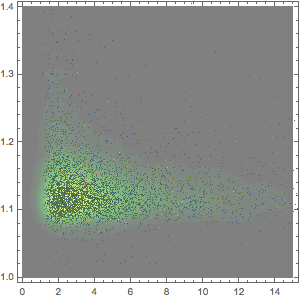
如以下对数绘图所示，每分钟的票房收入为一个更加剧烈波动的函数.

In[6]:=

profitPerMinute = TimeSeries[{#[[1, 4]], Mean[#6/#3 & @@@ #]} & /@ Split[SortBy[ Cases[movieData, {_, _, _Quantity, _DateObject, _, _Quantity}], \ #[[4]] &], #1[[4]] === #2[[4]] &]];

In[7]:=

DateListLogPlot[MovingAverage[profitPerMinute, Quantity[1, "Months"]], FrameLabel -> Automatic, PlotLabel -> "box office receipts per film minute", AxesOrigin -> {DateObject[{2000, 1, 1}], 0}, PlotRange -> {{DateObject[{2000, 1, 1}], DateObject[{2015, 12, 31}]}, All}]

Out[7]=

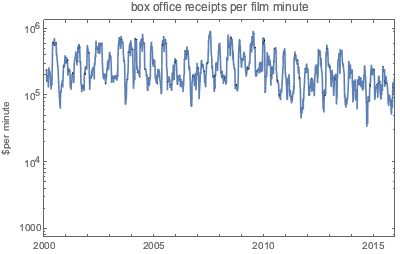
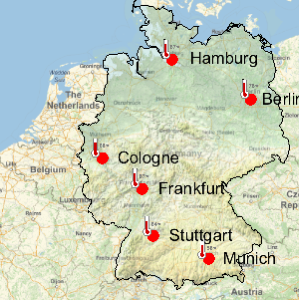
在近 15 年内，电影的平均播放时间基本相同.

In[8]:=

averageRuntimes = {#[[1, 1]], Mean[#[[All, -1]]]} & /@ Split[Sort[{DateObject[{#4["Year"]}], UnitConvert[#3, "Minutes"]} & @@@ Cases[movieData, {_, _, _Quantity, _DateObject, _, _}]], #1[[ 1]] === #2[[1]] &];

In[9]:=

DateListPlot[averageRuntimes, FrameLabel -> Automatic, PlotLabel -> "average runtime", AxesOrigin -> {DateObject[{2000, 1, 1}], 0}]

Out[9]=

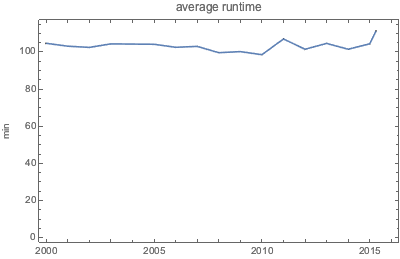
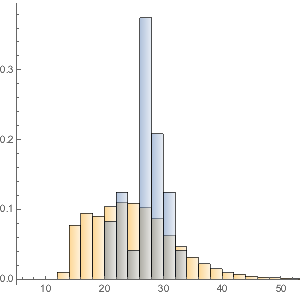
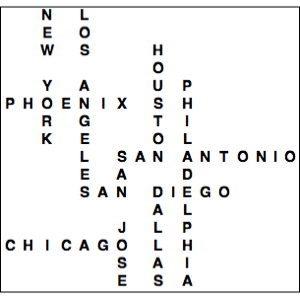
更详细的观察，电影的播放时间分布表现的相对平滑.

In[10]:=

movieRuntimes = DeleteMissing[movieData[[All, 3]]];

In[11]:=

hg = Histogram[movieRuntimes, {1, 200, 5}, "PDF", AxesLabel -> Automatic]

Out[11]=

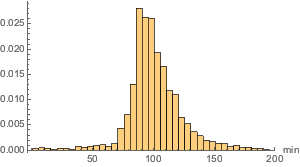
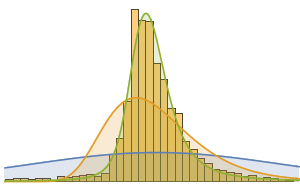
应用大量内置分布的建模表明 Lévy 稳定分布最为接近. 这里，用正态（从独立分布中独立抽样的随机变量的平均值分布）、对数正态（许多独立正值的随机变量的乘积结果分布）和稳定分布进行拟合计算.

In[12]:=

edNormal = EstimatedDistribution[movieRuntimes, NormalDistribution[\[Mu], \[Sigma]]]

Out[12]=

In[13]:=

edLogNormal = EstimatedDistribution[movieRuntimes, LogNormalDistribution[\[Mu], \[Sigma]]]

Out[13]=

In[14]:=

edStable = EstimatedDistribution[movieRuntimes, StableDistribution[1, \[Alpha], \[Beta], \[Mu], \[Sigma]]]

Out[14]=

有趣的是，稳定分布从视觉上是最佳拟合.

仅有少数几个人工对象不服从稳定分布. 稳定分布的一个特点在于出现相对较多的异常值，通常比均值大几倍. 电影满足这一特点. 以下为2000年 1月 1日 以后上映的（以播放时间计算）最长的电影：

In[15]:=

longest = EntityClass[ "Movie", {EntityProperty["Movie", "ReleaseDate"] -> Between[{DateObject[{2000}], DateObject[{2015}]}], EntityProperty["Movie", "Runtime"] -> TakeLargest[10]}] // EntityList

Out[15]=

在表格中总结.

In[16]:=

With[{props = {EntityProperty["Movie", "Name"], EntityProperty["Movie", "Genres"], EntityProperty["Movie", "Runtime"], EntityProperty["Movie", "ReleaseDate"]}}, TextGrid[Prepend[EntityValue[longest, props], props], Dividers -> All, Alignment -> Left, Background -> {None, {LightBlue}}]] // TraditionalForm

Out[16]//TraditionalForm=