Информация о фильмах

База знаний Wolfram Knowledgebase позволяет изучить поминутную стоимость и кассовые сборы от фильмов, выпущенных с 2000 года. Кроме того, вы можете получить информацию о средней продолжительности проката фильмов, которая подчиняется закону так называемого устойчивого распределения, что необычно для объектов, созданных человеком.

Воспользуемся неявно определенным классом сущностей, чтобы выбрать фильмы, выпущенные с начала данного тысячелетия.

In[1]:=

Length[movies = EntityClass["Movie", EntityProperty["Movie", "ReleaseDate"] -> Between[{DateObject[{2000}], DateObject[{2015}]}]] // EntityList]

Out[1]=

Извлечем названия фильмов, жанры, срок проката, производственные бюджеты и кассовые сборы.

In[2]:=

movieData = EntityValue[ movies, {EntityProperty["Movie", "Name"], EntityProperty["Movie", "Genres"], EntityProperty["Movie", "Runtime"], EntityProperty["Movie", "ReleaseDate"], EntityProperty["Movie", "ProductionBudget"], EntityProperty["Movie", "DomesticBoxOfficeGross"]}];

Стоимость минуты фильма, вышедшего в прокат, является функцией с значением, колеблющимся во времени.

In[3]:=

costPerMinute = TimeSeries[{#[[1, 4]], Mean[#5/#3 & @@@ #]} & /@ Split[SortBy[ Cases[movieData, {_, _, _Quantity, _DateObject, _Quantity, _}], \ #[[4]] &], #1[[4]] === #2[[4]] &]];

In[4]:=

DateListLogPlot[costPerMinute, FrameLabel -> Automatic, PlotLabel -> "average cost per minute", AxesOrigin -> {DateObject[{2000, 1, 1}], 0}]

Out[4]=

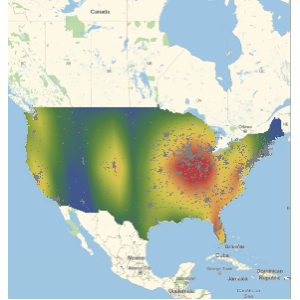
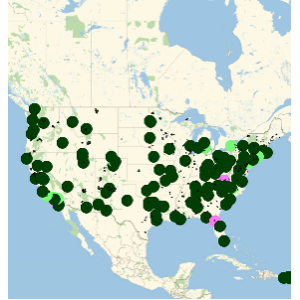
Тем не менее, в среднем за месяц, некоторые периодичные элементы в распределении стоимости за минуту проката становятся видимыми. В частности, на следующем графике зеленые линии сетки обозначают День Независимости США; фиолетовые линии соответствуют Дню Благодарения.

In[5]:=

DateListPlot[MovingAverage[costPerMinute, Quantity[1, "Months"]], FrameLabel -> Automatic, PlotLabel -> "average cost per minute", AxesOrigin -> {DateObject[{2000, 1, 1}], 0}, GridLines -> {Join[{#, Darker[Green]} & /@ Table[DateObject[{y, 7, 4}], {y, 2000, 2015}], {#, Darker[Purple]} & /@ Table[DateObject@ WolframAlpha[ "Thanksgiving " <> IntegerString[y], {{"Result", 1}, "ComputableData"}], {y, 2000, 2015}]], None}]

Out[5]=

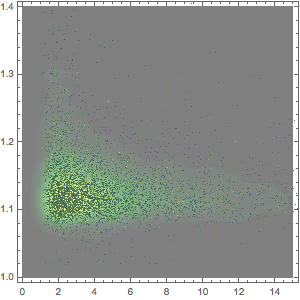
Как показано на следующем логарифмическом графике, кассовые сборы за минуту проката представляют собой еще более колеблющуюся функцию.

In[6]:=

profitPerMinute = TimeSeries[{#[[1, 4]], Mean[#6/#3 & @@@ #]} & /@ Split[SortBy[ Cases[movieData, {_, _, _Quantity, _DateObject, _, _Quantity}], \ #[[4]] &], #1[[4]] === #2[[4]] &]];

In[7]:=

DateListLogPlot[MovingAverage[profitPerMinute, Quantity[1, "Months"]], FrameLabel -> Automatic, PlotLabel -> "box office receipts per film minute", AxesOrigin -> {DateObject[{2000, 1, 1}], 0}, PlotRange -> {{DateObject[{2000, 1, 1}], DateObject[{2015, 12, 31}]}, All}]

Out[7]=

Среднее время проката фильмов было достаточно постоянно в течение последних 15 лет.

In[8]:=

averageRuntimes = {#[[1, 1]], Mean[#[[All, -1]]]} & /@ Split[Sort[{DateObject[{#4["Year"]}], UnitConvert[#3, "Minutes"]} & @@@ Cases[movieData, {_, _, _Quantity, _DateObject, _, _}]], #1[[ 1]] === #2[[1]] &];

In[9]:=

DateListPlot[averageRuntimes, FrameLabel -> Automatic, PlotLabel -> "average runtime", AxesOrigin -> {DateObject[{2000, 1, 1}], 0}]

Out[9]=

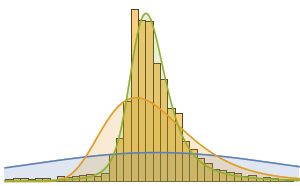
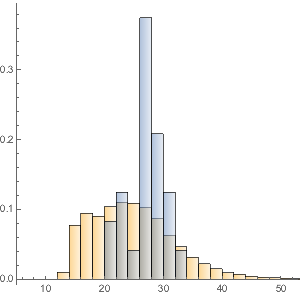
Распределение времени проката представляет собой oтносительно гладкую функцию.

In[10]:=

movieRuntimes = DeleteMissing[movieData[[All, 3]]];

In[11]:=

hg = Histogram[movieRuntimes, {1, 200, 5}, "PDF", AxesLabel -> Automatic]

Out[11]=

Моделирование с использованием большого количества встроенных распределений указывает на то, что ближе всего для данных подходит стабильное распределение Леви. В данном случае, рассчитаем совместимость данных о фильмах с нормальным (распределение средних значений случайных величин независимых друг от друга и извлеченных из независимых распределений), логнормальным (распределение произведения многих независимых положительных случайных величин), и устойчивым распределениями.

In[12]:=

edNormal = EstimatedDistribution[movieRuntimes, NormalDistribution[\[Mu], \[Sigma]]]

Out[12]=

In[13]:=

edLogNormal = EstimatedDistribution[movieRuntimes, LogNormalDistribution[\[Mu], \[Sigma]]]

Out[13]=

In[14]:=

edStable = EstimatedDistribution[movieRuntimes, StableDistribution[1, \[Alpha], \[Beta], \[Mu], \[Sigma]]]

Out[14]=

Отметим, что устойчивое распределение визуально наиболее точно соответствует распределению данных о фильмах.

In[15]:=

Show[{hg, ListLinePlot[ Table[{x, #}, {x, Quantity[0, "Minutes"], Quantity[200, "Minutes"], Quantity[1, "Minutes"]}] & /@ {PDF[edNormal, x], PDF[edLogNormal, x], PDF[edStable, x]}, PlotLegends -> {"normal", "lognormal", "stable"}, Filling -> Axis, PlotRange -> All]}]

Out[15]=

Лишь немногие созданные человеком объекты имеют свойства стабильного распределения. Характерной чертой стабильного распределения является наличие крайних величин, часто в несколько раз превышающих среднее значение распределения. Эта характеристика наблюдается благодаря фильмам. Рассмотрим, 10 фильмов с самoй большой продолжительностью, выпущенных после 1 января 2000 года.

In[16]:=

longest = EntityClass[ "Movie", {EntityProperty["Movie", "ReleaseDate"] -> Between[{DateObject[{2000}], DateObject[{2015}]}], EntityProperty["Movie", "Runtime"] -> TakeLargest[10]}] // EntityList

Out[16]=

Представим результаты в виде таблицы.

In[17]:=

With[{props = {EntityProperty["Movie", "Name"], EntityProperty["Movie", "Genres"], EntityProperty["Movie", "Runtime"], EntityProperty["Movie", "ReleaseDate"]}}, TextGrid[Prepend[EntityValue[longest, props], props], Dividers -> All, Alignment -> Left, Background -> {None, {LightBlue}}]] // TraditionalForm

Out[17]//TraditionalForm=