Wolfram Mathematica

Integral Transform EntityStore

An integral transform is a mathematical operation that maps one function 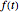to another 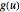by means of an integral of the form 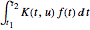where 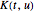is known as the kernel. Integral transforms are extremely important in many areas of interest, including signal processing, medical imaging, and probability theory. Here, the construction of an entity store containing properties of important transforms is illustrated.

The entity store can be hand-coded by recording the most important properties of integral transforms in an EntityStore data structure.

In[1]:=

EntityStore[<| "Types" -> <| "IntegralTransform" -> <| "Entities" -> <| "ExponentialFourierTransform" -> <| "Label" -> "exponential Fourier transform", "StandardName" -> "ExponentialFourierTransform", "StandardNotation" -> Hold[f[t]], "Definition" -> Inactive[FourierTransform][f[t], t, z] \!\(\* TagBox["==", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"=="]\) Inactive[Integrate][ E^(I t z) f[t], {t, -\[Infinity], \[Infinity]}]/Sqrt[ 2 \[Pi]], "GeneralProperties" -> <| "Linearity" -> {Inactive[FourierTransform][ a f[t] + b g[t], t, z] \!\(\* TagBox["==", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"=="]\) a Inactive[FourierTransform][f[t], t, z] + b Inactive[FourierTransform][g[t], t, z], Inactive[FourierTransform][f[t], t, z] \!\(\* TagBox["==", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"=="]\) Inactive[FourierTransform][f[-t] UnitStep[t], t, -z] + Inactive[FourierTransform][f[t] UnitStep[t], t, z]}, "Reflection" -> {Inactive[FourierTransform][f[-t], t, z] \!\(\* TagBox["==", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"=="]\) Inactive[FourierTransform][f[t], t, -z]}, "Dilation" -> {ConditionalExpression[ Inactive[FourierTransform][f[a t], t, z] \!\(\* TagBox["==", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"=="]\) Inactive[FourierTransform][f[t], t, z/a]/Abs[a], a \!\(\* TagBox["\[Element]", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"\[Element]"]\) Reals && a \!\(\* TagBox["!=", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"!="]\) 0]}, "Shifting or translation" -> {ConditionalExpression[ Inactive[FourierTransform][f[-a + t], t, z] \!\(\* TagBox["==", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"=="]\) E^(I a z) Inactive[FourierTransform][f[t], t, z], a \!\(\* TagBox["\[Element]", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"\[Element]"]\) Reals]}|>|>|>|>|>|>]

Out[1]=

A more complete version can be retrieved from the following CloudObject.

In[2]:=

itstore = CloudGet[CloudObject[ "https://www.wolframcloud.com/objects/c21b356b-607a-406c-af91-\ 5088f435fe99"]]

Out[2]=

Register the store for this session.

In[3]:=

PrependTo[$EntityStores, itstore];

View entities in the store.

In[4]:=

EntityValue["IntegralTransform", "Entities"]

Out[4]=

Add a new transform.

In[5]:=

Entity["IntegralTransform", "HilbertTransform"]["Label"] = "Hilbert transform"; Entity["IntegralTransform", "HilbertTransform"]["Definition"] = Inactive[HilbertTransform][f[t], t, x] \!\(\* TagBox["==", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"=="]\) 1/\[Pi] Inactive[Integrate][f[t]/( t - x), {t, -\[Infinity], \[Infinity]}, PrincipalValue -> True, Assumptions -> x \!\(\* TagBox["\[Element]", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"\[Element]"]\) Reals];

Return the currently available properties for integral transforms.

In[6]:=

EntityValue["IntegralTransform", "Properties"]

Out[6]=

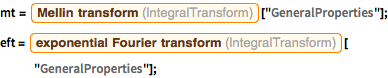
Retrieve the definitions for exponential Fourier and Mellin transforms.

In[7]:=

EntityValue[ Entity["IntegralTransform", "LaplaceTransform"], "Definition"]

Out[7]=

In[8]:=

EntityValue[ Entity["IntegralTransform", "MellinTransform"], "Definition"]

Out[8]=

Compare with the expressions returned by corresponding built‐in functions.

In[9]:=

Activate[EntityValue[Entity["IntegralTransform", "LaplaceTransform"], "Definition"][[2]] /. f :> Function[t, ArcTan[t]]]

Out[9]=

In[10]:=

LaplaceTransform[ArcTan[t], t, z]

Out[10]=

Display the convolution property of the Z-transform.

In[11]:=

Entity["IntegralTransform", "ZTransform"][ "GeneralProperties"]["Convolution"]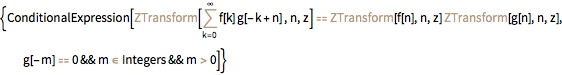

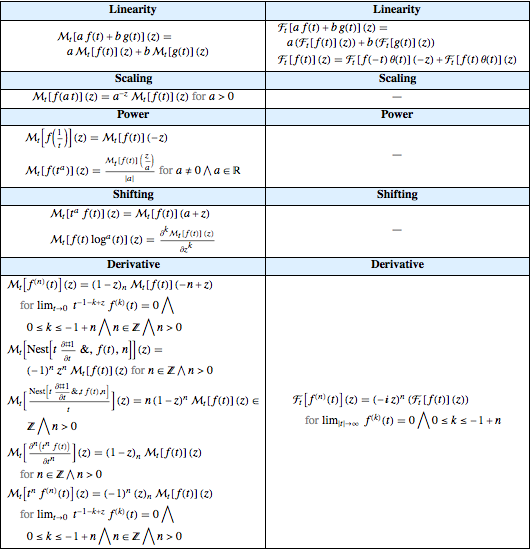
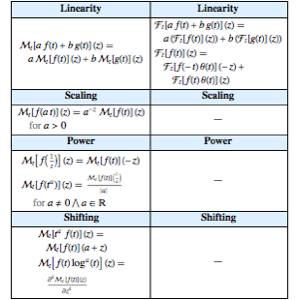
Out[11]=

Compare the currently stored properties of the exponential Fourier and Mellin transforms.

In[12]:=

format[l_] := If[MatchQ[l, _Missing], "\[LongDash]", Activate[HoldForm @@ ({Column[l]} /. HoldPattern[ConditionalExpression[a_, b_]] :> Row[{a, Style[ " for ", Gray], b}])]]

In[13]:=

mt = Entity["IntegralTransform", "MellinTransform"][ "GeneralProperties"]; eft = Entity["IntegralTransform", "ExponentialFourierTransform"][ "GeneralProperties"];

In[14]:=

Grid[Take[ Flatten[{{Style[#, Bold], Style[#, Bold]}, {format@mt[#], format@eft[#]}} & /@ DeleteDuplicates[Join[Keys[mt], Keys[eft]]], 1], 10], Dividers -> All, Background -> {None, {{LightBlue, White}}}] // TraditionalForm

Out[14]//TraditionalForm=