Fallbeschleunigung schätzen

Die Fallbeschleunigung kann durch die Messung der Schwingungsdauer eines Pendels 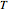und dessen Länge 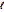mit der Formel 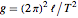berechnet werden. Die Messunsicherheit im Durchschnitt von fünf wiederholten Messungen der Schwingungsdauer wird mit BatesDistribution modelliert.

In[1]:=

\[Mu]T = Quantity[2, "Seconds"]; \[CapitalDelta]T = Quantity[0.01, "Seconds"]; period\[ScriptCapitalD] = BatesDistribution[ 5, {\[Mu]T - \[CapitalDelta]T/2, \[Mu]T + \[CapitalDelta]T/2}]

Out[1]=

Die Länge des Pendulums wurde mit einem Maßstab mit der Auflösung 1 mm gemessen, daher wurde die Messunsicherheit mit UniformDistribution modelliert.

In[2]:=

\[Mu]len = Quantity[1, "Meters"]; \[CapitalDelta]len = UnitConvert[Quantity[1, "mm"], "Meters"]; len\[ScriptCapitalD] = UniformDistribution[{\[Mu]len - \[CapitalDelta]len/ 2., \[Mu]len + \[CapitalDelta]len/2.}]

Out[2]=

Die Messunsicherheit beim Messen der Fallbeschleunigung.

In[3]:=

g\[ScriptCapitalD] = TransformedDistribution[ (2 \[Pi])^2 len/T^2, {len \[Distributed] len\[ScriptCapitalD], T \[Distributed] period\[ScriptCapitalD]}]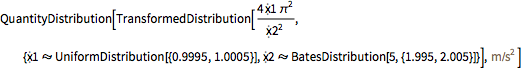

Out[3]=

Vergleichen Sie diese mit der linearen Approximation.

In[4]:=

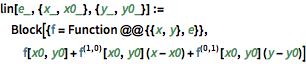
lin[e_, {x_, x0_}, {y_, y0_}] := Block[{f = Function @@ {{x, y}, e}}, f[x0, y0] + \!\(\*SuperscriptBox[\(f\), TagBox[ RowBox[{"(", RowBox[{"1", ",", "0"}], ")"}], Derivative], MultilineFunction->None]\)[x0, y0] (x - x0) + \!\(\*SuperscriptBox[\(f\), TagBox[ RowBox[{"(", RowBox[{"0", ",", "1"}], ")"}], Derivative], MultilineFunction->None]\)[x0, y0] (y - y0)]

In[5]:=

lin\[ScriptCapitalD][\[ScriptCapitalD]_] := NormalDistribution[Mean[\[ScriptCapitalD]], StandardDeviation[\[ScriptCapitalD]]]

In[6]:=

gApprox\[ScriptCapitalD] = TransformedDistribution[ lin[(2 Pi)^2 len/ T^2, {len, \[Mu]len}, {T, \[Mu]T}], {len \[Distributed] lin\[ScriptCapitalD][len\[ScriptCapitalD]], T \[Distributed] lin\[ScriptCapitalD][period\[ScriptCapitalD]]}]

Out[6]=

Berechen Sie die durchschnittliche Fallbeschleunigung mithilfe der exakten und linearisierten Verteilung.

In[7]:=

{\[Mu]g, \[Mu]gApprox} = {NExpectation[g, g \[Distributed] g\[ScriptCapitalD]], NExpectation[g, g \[Distributed] gApprox\[ScriptCapitalD]]}

Out[7]=

Berechen Sie die Ausmaße der Messunsicherheit.

In[8]:=

{\[Sigma]g, \[Sigma]gApprox} = {Sqrt[ NExpectation[(g - \[Mu]g)^2, g \[Distributed] g\[ScriptCapitalD]]], StandardDeviation[gApprox\[ScriptCapitalD]]}

Out[8]=

Ermitteln Sie die Schätzung des Konfidenzintervalls von 90% der gemessenen Beschleunigung.

In[9]:=

confidenceInterval = Quantile[RandomVariate[g\[ScriptCapitalD], 10^6], {0.05, 0.95}]

Out[9]=

In[10]:=

NProbability[First[confidenceInterval] < x < Last[confidenceInterval], x \[Distributed] g\[ScriptCapitalD]]

Out[10]=