Die Zeitgleichung
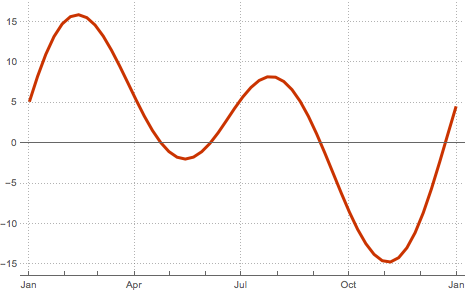
Aufgrund der Exzentrizität der Erdumlaufbahn und der Neigung der Erdachse in Bezug auf die Ebene der Umlaufbahn variiert die scheinbare Bewegung der Sonne im Laufe des Jahres. Dies bedeutet einen Unterschied zwischen der Zeit, die von einer Sonnenuhr gemessen wird (scheinbare Sonnenzeit) und jener, die von einer präziseren Uhr wie zum Beispiel einer, die auf der scheinbaren Drehung der Erde vor einem Fixsternhintergrund basiert (Sternzeit), gemessen wird. Diese Differenz ist bekannt als die Zeitgleichung.
SiderealTime gibt Werte der Sternzeit mithilfe von MixedUnit als gemischte Einheiten zurück.
SiderealTime[]SiderealTime[];
QuantityUnit[%]Die Sternzeit ist eigentlich ein Winkel und kann daher in andere Winkeleinheiten zerlegt werden.
UnitConvert[SiderealTime[], "AngularDegrees"]Die Zeitgleichung wird durch die Bewegung der Sonne bestimmt, gegeben durch SunPosition. Berechnen Sie die wöchentlichen Werte zu GMT-Mittagszeit.

dates = DateRange[
DateObject[{2015, 1, 1}, TimeObject[{12, 0}, TimeZone -> 0],
TimeZone -> 0.`],
DateObject[{2015, 12, 31}, TimeObject[{12, 0}, TimeZone -> 0],
TimeZone -> 0.`], 7];sunpos = SunPosition[GeoPosition[{0, 0}], dates,
CelestialSystem -> "Equatorial"]Verwenden Sie SiderealTime, um die Rektaszension am Greenwich-Meridian immer am selben Wochentag zu berechnen.
stime = SiderealTime[GeoPosition[{0, 0}], dates]Ermitteln Sie schließlich die entsprechenden Werte der Zeitgleichung als die Differenz zwischen der Rektaszension der Sonne und der Sternzeit jeweils zu Mittag im Laufe eines Jahres. Drücken Sie das Ergebnis in Minuten aus.
equationoftime =
UnitConvert[(TimeSeriesMap[First, sunpos] - stime),
"MinutesOfRightAscension"]Die absoluten Werte der Zeitgleichung können größer als 15 Minuten sein.
MinMax[equationoftime]